Alberto Mercado Saucedo

Fueron varias las fronteras que cruzó Roberto Frucht tanto en las matemáticas como en su trayectoria personal. Obtuvo resultados de gran importancia y profunda belleza en teoría de grafos, cuando esta área recién comenzaba a definirse como tal en el medio académico internacional, y fue autor de algunos de los primeros artículos de investigación matemática realizada en Chile, publicados en revistas internacionales en los años cuarenta del siglo veinte. Además, dejó cantidad de gratos recuerdos entre colegas y estudiantes de la Universidad Técnica Federico Santa María –UTFSM- en Valparaíso, donde fue profesor durante más de medio siglo.

Hace un tiempo tuve la oportunidad de presenciar un bello e inesperado testimonio del poeta Raúl Zurita, que estudió ingeniería a fines de los años sesenta y tuvo a Frucht como profesor. El 2015 Zurita recibió el doctorado honoris causa de la universidad, y en su discurso de aceptación dedicó varios minutos a recordar una clase dictada por un “profesor ya mayor, de baja estatura” en la que el entonces futuro poeta se encontró con la “elegancia, simpleza y belleza” de cierta fórmula matemática. Como si la clase ocurriera en esos momentos, la voz del poeta recordó el áspero andar de la tiza en el pizarrón de cuarenta años atrás: el profesor Roberto Frucht explicando a sus estudiantes la fórmula de Euler, e^iπ+1=0, quizá una de las expresiones más hermosas de la matemática, como bien lo percibió Zurita.

¿Dónde reside la belleza de esta fórmula? Quizá simplemente en que aparecen distintos números bien conocidos: los irracionales e y π, junto con el imaginario i, la raíz cuadrada de -1, relacionados por operaciones matemáticas. Pero también podemos pensar que la fórmula relaciona los mundos del álgebra y la geometría: expresa que el número -1 hace ángulo con el eje x en el plano complejo; lo mismo ocurre con el valor de para cualquier ángulo. Quizá fueron estos cruces lo que impactó a Zurita y provocó tan duradero recuerdo.

De hecho, la obra literaria de Zurita hace recurrentes alusiones al mundo de las matemáticas, tema del que no hablaremos ahora pero que podemos conjeturar se originó en momentos iluminadores como el anterior, que en el discurso del poeta tuvo un trágico contrapunto en la alusión al golpe de estado y el inicio de la dictadura, lo cual afectó directamente a Zurita y dejó al pueblo chileno un triste legado, aún vigente en nuestros días. Precisamente, el profesor Frucht había llegado a Sudamérica treinta años antes huyendo de horrores similares.

Roberto Frucht nació el 9 de agosto de 1906 en Brno, ciudad que hoy pertenece a la República Checa, y luego vivió en Berlin desde los dos años de edad, cuando su familia se instaló en la ciudad alemana. Allí finalizó estudios universitarios y decidió continuar especializándose en matemáticas, para lo que obtuvo su doctorado en 1930 en teoría de grupos, área del álgebra abstracta. Obtener una de las escasas plazas en la universidad era sumamente difícil, e impartir clase en un Gimnasium (colegio) estaba reservado para los alemanes, nacionalidad que no poseía Frucht. Estas circunstancias, por no hablar del contexto internacional, de lo más complicado para un descendiente de familia judía, hicieron que en 1930 se trasladara a Trieste, Italia, donde trabajaría en una compañía de seguros por casi ocho años. Allí, inició una relación con María Mercedes Bertogna, compañera de trabajo de origen argentino, con quien se casó en 1932.

Podemos imaginar que durante esos años en Trieste el trabajo de Roberto era rutinario, pero se las ingenió para publicar artículos -escritos en alemán- sobre la investigación realizada en su doctorado, además de otros trabajos de contabilidad escritos en italiano. Pero lo mejor estaba por venir, pues un día cualquiera de 1936 un hecho fortuito determinó la trayectoria de Roberto Frucht: recibió en su oficina de seguros un catálogo con información de un libro del matemático húngaro Dénes Kőnig sobre teoría de grafos, prácticamente el primero sobre la materia, y se interesó por el título de un capítulo que era algo así como “aplicaciones de la teoría de grupos a los grafos”. Ordenó el libro y desde que lo recibió se convirtió, según sus propias palabras, en un entusiasta de la teoría de grafos. Tan fue así, que se dedicó a estudiar el tema en detalle y en especial a trabajar en los problemas abiertos planteados en el libro.

Para comprender la idea de esta área de las matemáticas, pensemos que un grafo es una colección de vértices junto con segmentos que los unen en una combinación dada, y es esta combinación lo que determina el grafo en particular. Por ejemplo un polígono: los triángulos, cuadrados y demás son grafos.

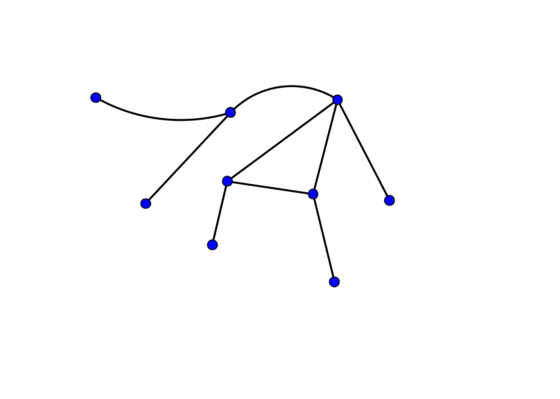
También es un grafo el diagrama del mapa del metro en una ciudad, si pensamos que cada estación es un vértice, que está unido con otro si es que hay una línea de metro entre las estaciones. Lo importante en un grafo es su estructura: el cómo se dan las conexiones, la combinación precisa, y no importan la longitud o la forma con que dibujemos sus segmentos. Es lo mismo que para el usuario del metro cuando lee el mapa, pues lo que le importa es saber si un par de vértices/estaciones dados están o no conectados.

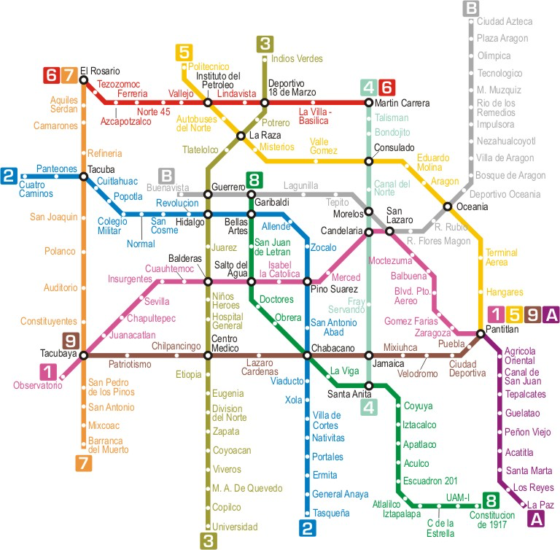
En teoría de grafos se estudian problemas planteados sobre estas estructuras, problemas que pueden ser geométricos, combinatorios, algebraicos o de otra índole. El tema en el que se interesó Frucht está relacionado con determinar el conjunto de automorfismos de un grafo, que son permutaciones entre los vértices que no cambian su estructura. Los automorfismos son una especie de simetrías del grafo respecto a sus conexiones, y son transformaciones que forman un grupo, pues se puede definir una operación entre dos de ellas: la composición, que consiste en aplicar una transformación y luego la otra. En el caso de un triángulo, es fácil ver que todas sus permutaciones son simetrías: ya sea realizar una especie de rotación entre los tres vértices o bien intercambiar dos de ellos como en una reflexión especular (el lector podrá determinar cuántos automorfismos hay).

Hacemos hincapié en que no es importante el largo o forma de los segmentos. Por ejemplo, el grafo con forma de pentágono mostrado abajo posee un solo automorfismo (además de la identidad), que consiste en intercambiar los vértices verdes uno con el otro, lo mismo que los vértices rojos también entre sí, dejando fijo el vértice de color azul.

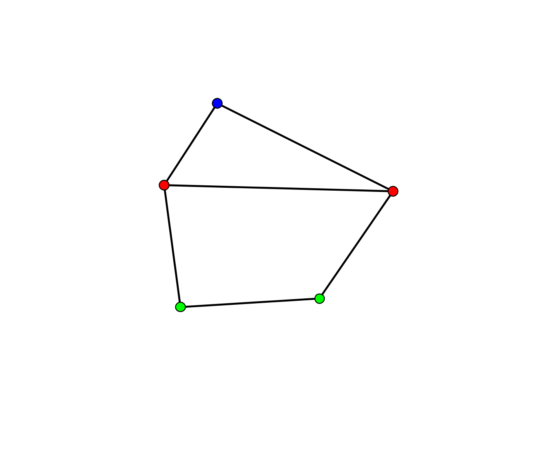
Tras estudiar el libro de teoría de grafos, uno de los primeros resultados de Roberto fue determinar el grupo de automorfismos de algunos sólidos platónicos (equivalente tridimensional de los polígonos regulares). Un año más tarde, resolvió un problema mucho más importante: König había planteado en su libro la pregunta abierta si dado un grupo finito cualquiera, éste corresponderá necesariamente a los automorfismos de un grafo, el que habría que determinar. Esto significa pasar del álgebra a la geometría, algo así como dibujar el grupo dado por medio de su grafo. Frucht respondió afirmativamente a esta pregunta, y definió un procedimiento constructivo para determinar el grafo a partir del grupo dado, lo que se conoce como Teorema de Frucht. Además, encontró un grafo especial: uno que no posee ninguna simetría más que la identidad. A este grafo se le conoce como Grafo de Frucht y se ha convertido en un ejemplo clásico en el área. Es mostrado en la siguiente figura, donde se puede notar que cada vértice posee exactamente tres conexiones; de hecho este es el grafo más pequeño con tal estructura y que no tiene automorfismos.

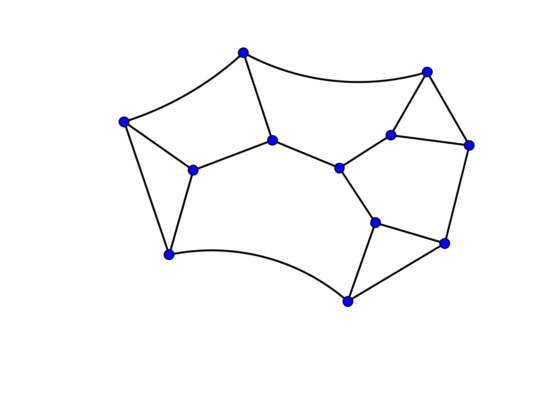
Frucht realizó estos trabajos entre 1936 y 1938, tristes años en Europa, en pleno auge del nazismo alemán y del fascismo italiano. Por esos años se aprobaron en Italia discriminadoras leyes raciales que complicaron la continuidad laboral de Roberto en Trieste. La familia, que ya incluía a su hija Érica, nacida en Trieste poco antes, decide mudarse a Argentina, donde vivían parientes de Mercedes. A principios de 1939 viajaron en el buque de vapor Augustus hasta el puerto de Buenos Aires, donde Frucht trabajó de nuevo en una compañía de seguros, pero también encontró la forma de seguir pensando en matemáticas, pues publicó varias notas sobre geometría diferencial en la revista de la Unión Matemática Argentina UMA, en ediciones bilingües en alemán y español.

De manera un tanto azarosa, la estadía en Buenos Aires llegó pronto a su fin, pues Roberto se encontró con la oportunidad de optar por una plaza como profesor en la UTFSM, institución que había sido recientemente creada y se abocaba a contratar un número de profesores extranjeros, sobre todo alemanes, para poder lograr rápidamente una masa crítica de académicos. Del Atlántico al Pacífico, seguramente la vida en el puerto de Valparaíso era más tranquila que en Trieste o Buenos Aires; en todo caso la familia se acostumbró sin dificultad a Valparaíso, excepto por los no poco frecuentes temblores, según Roberto contaba, un poco en tono de broma, a sus cercanos.

Roberto continuó publicando algunas notas sobre geometría diferencial y álgebra en revistas de la UMA, escritas en español y ahora con afiliación UTFSM. Retomó su trabajo en teoría de grafos gracias a una invitación del matemático Harold S.M. Coxeter para contribuir al recién creado Canadian Journal of Mathematics, para lo que se dispuso a trabajar contra el tiempo, y logró obtener interesantes refinamientos de sus resultados anteriores y publicar un artículo en 1949.

Durante las décadas que siguieron, Roberto Frucht continuó con su investigación en teoría de grafos y se convirtió en uno de los pioneros de la matemática en Chile. Fue decano de la Facultad de Ciencias de la universidad entre 1948 y 1968, director y miembro fundador de la Sociedad de Matemáticas de Chile SOMACHI, colaborador frecuente de la revista local Scientia, entre otras labores académicas, y en 1970 fue nombrado profesor emérito. Desde entonces y hasta poco antes de su fallecimiento en 1997 continuó impartiendo clases en la universidad, como aquella donde enseñó la formula de Euler y transmitió a sus alumnos, en las palabras del poeta que entonces ocupaba un pupitre de estudiante anónimo, la irremediable melancolía de lo que nos parece extremadamente bello.

Referencias:

Gary Chartrand, Ping Zhang. A First Course in Graph Theory. Dover Publications 2012.

R. Frucht. Herstellung von Graphen mit vorgegebener abstrakter Gruppe

Compositio Mathematica, tome 6 (1939), p. 239-250.

Robert Frucht. Graphs of degree three with a given abstract group. Canad. J. Math. 1 (1949), 365–378.

Roberto W. Frucht. (1982). How I became interested in graphs and groups. Journal of Graph Theory. 6(2), 101-104 https://doi.org/10.1002/jgt.3190060203

Harary, F. (1982). Homage to roberto frucht. Journal of Graph Theory, 6(2), 97–99. https://doi:10.1002/jgt.3190060202

Héctor Hevia. Grafos con grupo dado de automorfismos. Proyecciones Vol 14 No 2 (1995).

Iván Szántó, Betsabe González. Breve reseña histórica de la Revista Scientia y las publicaciones de Matemática en Chile. Boletín de la Asociación Matemática Venezolana, Vol. XXI, No. 1 (2014).

Reinhard Siegmund-Schultze. Mathematicians Fleeing from Nazi Germany Individual Fates and Global Impact. Princeton university press. 2009.

Raúl Zurita Canessa. No nos hemos perdido (Discurso). Cuadernos de Educación. Publicación Trimestral Gratuita – ISSN 0719-0271. N 35, 2016.

Sobre el autor: Alberto Mercado Saucedo es profesor de matemáticas en la Universidad Técnica Federico Santa María (Valparaíso, Chile)

Sobre la ilustradora: Constanza Rojas Molina es profesora del departamento de matemáticas de la CY Cergy Paris Université (Cergy-Pontoise, Francia)