Las curiosas reglas de divisibilidad
Las reglas de divisibilidad de la aritmética parecen pequeños trucos de magia que nos permiten conocer, de forma más o menos rápida, si un cierto número, por ejemplo, 1.056.475.343, es divisible por 2, 3, 4, 5, 7 u otros números. Aunque nos puedan parecer una tontería, e incluso una simple anécdota matemática, estas reglas son muy útiles. A continuación, mostramos a modo de ejemplo algunas sencillas aplicaciones de algunas de las reglas de divisibilidad.
En más de una ocasión hemos hablado en esta sección del Cuaderno de Cultura Científica de los números primos, aquellos que solamente son divisibles por el 1 y por ellos mismos, como el 2, el 3 o el 11, pero no el 6, divisible también por 2 y 3, como en la entrada Buscando lagunas de números primos o Poema de los números primos. Un resultado sobre números primos fruto de una de las reglas de divisibilidad es el siguiente.
Propiedad 1: No existe ningún número pandigital (recordemos que estos son aquellos que están formados por todas las cifras básicas, con o sin el cero, como 934.521.687 ó 6.054.392.187) que sea un número primo.
También hemos puesto nuestra atención en los números capicúas o palíndromos, en la entrada El secreto de los números que querían ser simétricos, de los que podemos obtener la siguiente propiedad.
Propiedad 2: Los números capicúas con un número par de dígitos son divisibles por 11. Por lo tanto, tampoco son números primos.
Las reglas de divisibilidad, como la del número 9, pueden utilizarse también para el diseño de trucos de magia como el que se explica en este video de la sección Una de mates del programa de televisión, dirigido por José A. Pérez, Órbita Laika, en su segunda temporada, y que me había enseñado mi compañero y amigo Pedro Alegría (UPV/EHU). Lo podéis ver aquí: Una de mates – magia matemática. Y la explicación la podéis encontrar también aquí: El número nueve en una noche de verano.
De la misma forma, hay problemas de ingenio o retos matemáticos relacionados con las reglas de divisibilidad, como el siguiente reto planteado por el matemático británico John Horton Conway (1937-2020), fallecido recientemente como consecuencia del covid-19.
Las diez divisibilidades: Sea el número de diez dígitos ABCDEFGHIJ con todos sus dígitos diferentes (es decir, es un número pandigital), que verifica que:
1. A es divisible por 1,
2. AB es divisible por 2,
3. ABC es divisible por 3,
4. ABCD es divisible por 4,
5. ABCDE es divisible por 5,
6. ABCDEF es divisible por 6,
7. ABCDEFG es divisible por 7,
8. ABCDEFGH es divisible por 8,
9. ABCDEFGHI es divisible por 9,
10. ABCDEFGHIJ es divisible por 10.
¿Cuál es el número ABCDEFGHIJ?

Pero vayamos a las reglas de divisibilidad. Vamos a empezar explicando las reglas en grupos de números relacionados entre sí, siguiendo la idea de Peter M. Higgins en su libro Number Story: From Counting to Cryptography.
Reglas de divisibilidad de 2, 5 y 10. Nuestro sistema de numeración es decimal, es decir, la base de numeración con la que trabajamos es 10. Los divisores de este número son 1, 2, 5 y el propio 10, de hecho, las reglas que vamos a mostrar aquí se podrían extender a cualquier base de numeración b y sus divisores, aunque en esta entrada no dejaremos la base 10 en ningún momento.
La regla de divisibilidad del 10: un número es divisible por 10 si su dígito de las unidades (el primero empezando por la derecha) es 0.
La regla de divisibilidad del 5: un número es divisible por 5 si su dígito de las unidades es 0 o 5.
La regla de divisibilidad del 2: un número es divisible por 2 si su dígito de las unidades es 0, 2, 4, 6 u 8.
De hecho, podríamos reescribir las tres reglas de la siguiente forma: Un número es divisible por 2, 5 o 10, respectivamente, si, y sólo si, lo es su dígito de las unidades. Notemos que decir que las unidades, que van de 0 a 9, son divisibles por 10 es lo mismo que decir que toman el valor 0.
Vamos a dar una pequeña justificación. En general, las reglas de divisibilidad se pueden demostrar utilizando la representación decimal de los números o la aritmética modular, aunque nosotros en esta entrada solo utilizaremos la primera.
Como sabemos, todo número N de n + 1 cifras, cuya representación decimal es N = an an–1 … a2 a1 a0, tiene el valor
![]()
Como todos los elementos de la derecha de la expresión anterior, salvo las unidades a0, son múltiplos de 10, entonces para que N sea múltiplo de 10 las unidades a0 tienen que tomar el valor 0. Más aún, como los múltiplos de 10, también lo son de 2 y 5, se deduce que N es múltiplo de 2 o 5, respectivamente, si, y sólo si, la cifra de las unidades a0 también lo es.
Claramente, el número 564.930 es divisible por 10, luego también por 2 y 5, el número 735 es divisible por 5, pero no lo es ni por 2, ni por 10, y el número 614 es divisible por 2, pero no por 5 o 10. Por otra parte, el número inicial 1.056.475.343 no se puede dividir por ninguno de los tres.
Reglas de divisibilidad de 4, 8, 16, … Los criterios de divisibilidad anteriores, para 2, 5 y 10, se pueden extender a las potencias de estos números de una forma sencilla. Empecemos con el número 4.
La regla de divisibilidad del 4: un número es divisible por 4 si, y sólo si, él número formado por los dos primeros dígitos de la derecha (decenas y unidades) es divisible por 4.
Así, el número 5.316 es divisible por 4, ya que el número formado por los dos primeros dígitos de la derecha -16- es divisible por 4, mientras que 3.414 no lo es, por no serlo 14.
La demostración de esta regla es similar a la vista en el apartado anterior. Si tenemos un número N = an an–1 … a2 a1 a0, entonces
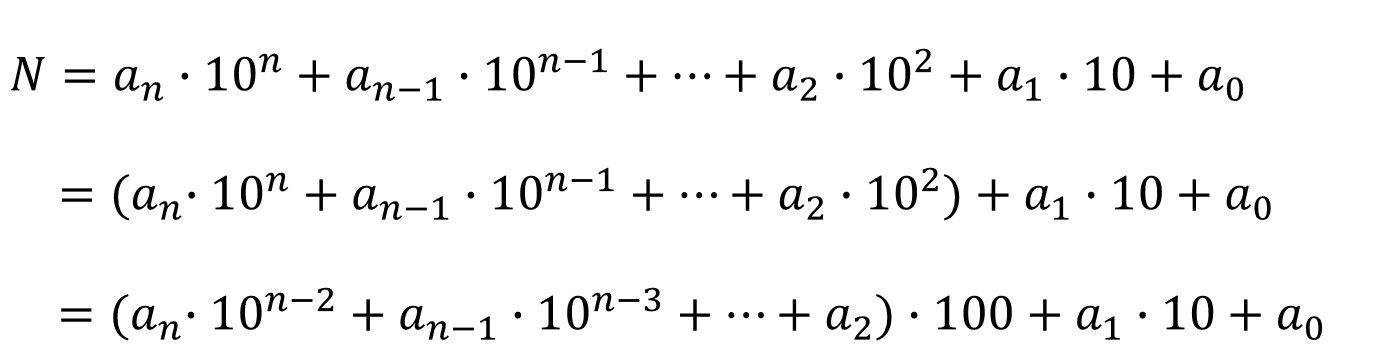
Como 100 es divisible por 4, se tiene que N será divisible por 4 si, y sólo si, a1 x 10 + a0 (el número representado por a1a0) es divisible por 4.
Teniendo en cuenta que 100 = 4 x 25, el argumento es válido para 4 (22), 25 (52) y 100 (102). Es decir, un número es divisible por 4, 25 o 100, respectivamente, si, y sólo si, el número formado por los dos dígitos de la derecha del número original, también lo es. Aunque en el caso de 100 lo que quiere decir es que los dos dígitos de la derecha son ceros.
Por ejemplo, el número 4.200 es divisible por 100, luego por todos los divisores de 100, el número 763.475 es divisible por 25, pero no por 100, ni por 4.
El argumento de la demostración anterior nos sirve para obtener una familia de reglas de divisibilidad generales para todas las potencias de 2, 5 y 10, que podemos formular como:
Un número es divisible por 2k, 5k o 10k, respectivamente, si, y sólo si, el número formado por los k dígitos de la derecha del número original, también lo es.
Por ejemplo, el número 54.237.983.152 es divisible por 16 (= 24) ya que el número formado por los cuatro dígitos de la derecha, 3.152 también se puede dividir por 16 (3.152 = 197 x 16). Lo curioso es que podemos seguir añadiendo dígitos a la izquierda del número para obtener números más grandes y la divisibilidad por 16 se mantendrá en todos ellos. Así, el número 712.834.554.237.983.152 sigue siendo divisible por 16, ya que la regla estudiada nos dice que solo importan los cuatro dígitos de la derecha (3.152).

Reglas de divisibilidad de 3, 6, 9, 12 y 15. Las reglas de divisibilidad del 3 y el 9 suelen ser de las pocas reglas, además de las de 2, 5 y 10, que suelen aprenderse en la escuela.
Mientras que las reglas anteriores implicaban solo a una pequeña parte del número, formado por cierto grupo de dígitos de su parte derecha, en los criterios de divisibilidad que vamos a ver ahora están implicados todos los dígitos del número.
La regla de divisibilidad del 3: un número es divisible por 3 si, y sólo si, la suma de sus dígitos es divisible por 3.
La demostración, haciendo uso de la representación posicional decimal de los números, es también muy sencilla. Si tenemos, de nuevo, un número N con n + 1 dígitos, N = an an–1 … a2 a1 a0, y le restamos la suma de sus dígitos, queda lo siguiente:
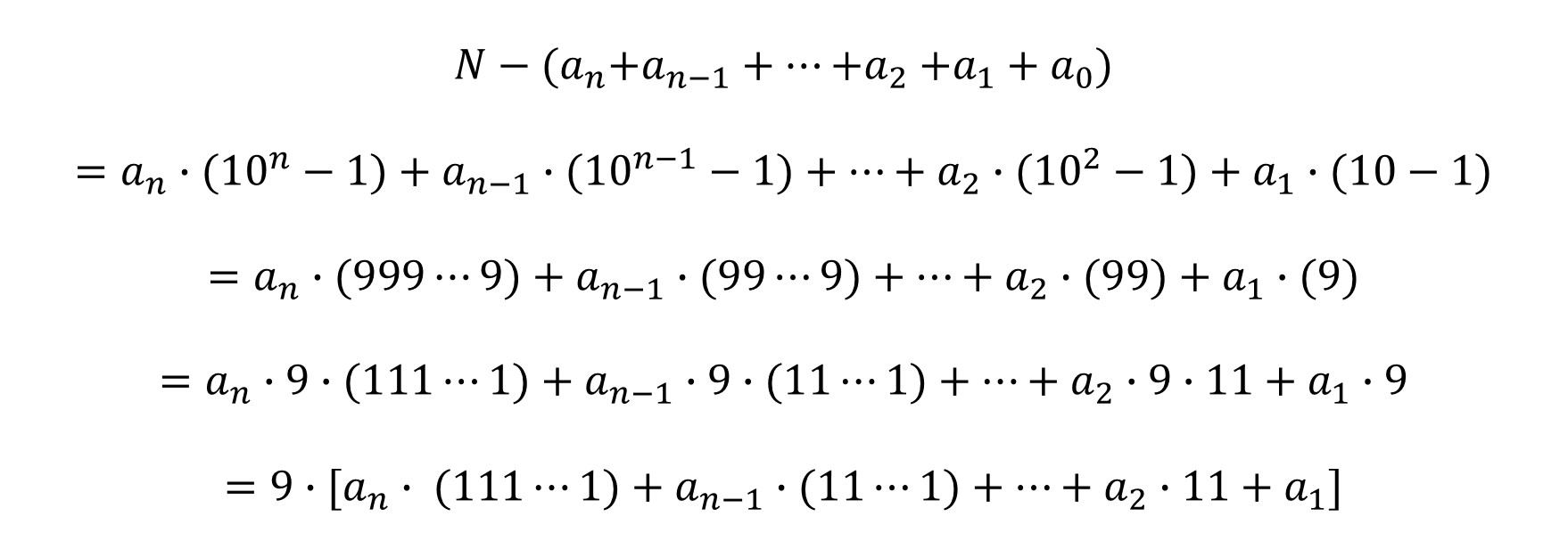
Como el resultado es múltiplo de 3, de hecho, también es múltiplo de 9, entonces el número N = an an–1 … a2 a1 a0 es divisible por 3 si, y sólo si, lo es también la suma de sus dígitos (an + an–1+ … + a2 + a1 + a0).
Veamos si el número del principio, 1.056.475.343, es divisible por 3. No lo es, ya que la suma de sus dígitos es 38, que no es divisible por 3. Por otro lado, el número 197.536.892.361 sí es divisible por 3, ya que a suma de sus dígitos es 60, claramente múltiplo de 3.
Como la condición que debe cumplir un número para ser divisible por 3 es que la suma de los dígitos del mismo también sea divisible por 3, se puede aplicar de nuevo la regla de divisibilidad a esta última cantidad, si fuese grande. Es decir, tenemos una regla que se puede aplicar de forma recursiva. Por ejemplo, para saber si el número 794.612.966.663.462.659.937 es divisible por 3, hay que sumar sus dígitos y esa suma es 116, pero a su vez para saber si este es divisible por 3 sumamos sus dígitos 1 + 1 + 6 = 8, cuyo resultado no es divisible por 3, luego tampoco el número enorme anterior.
Además, el argumento que se ha realizado para el número 3 demuestra lo mismo para el número 9.
La regla de divisibilidad del 9: un número es divisible por 9 si, y sólo si, la suma de sus dígitos es divisible por 9.
Ya estamos en condiciones de demostrar la propiedad 1 enunciada al principio de esta entrada del Cuaderno de Cultura Científica: No existe ningún número pandigital que sea un número primo. El motivo es que la suma de los dígitos de un número pandigital es 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, que es múltiplo de 9, luego cualquier número pandigital es múltiplo de 9, luego no es primo.
Por otra parte, el truco de magia de la serie Una de mates (Órbita Laika) que mencionábamos antes, está basado en esta regla del 9, como se explicaba.
Veamos una variante de ese truco. Se pide a una persona que piense –y escriba en un papel– un número de cinco o seis dígitos, aunque puede ser otra cantidad de dígitos. Por ejemplo, el número 632.571. Se puede enseñar el número a las demás personas “al resto del público”, pero no a la persona que le hace el truco. Después se le pide que cambie, a su gusto, el orden de los dígitos del número. Por ejemplo, 521.736. Y, además, que reste el mayor del menor, 632.571 – 521.736 = 110.835. A continuación, se le pide que elija uno de los dígitos no nulos del número que ha resultado de la resta. Supongamos que elige el 1. Lo siguiente es que diga en alto el resto de los dígitos y la persona que hace el truco adivinará, por arte de magia, el dígito que falta. La clave está en que el número resultante de la resta, en el ejemplo, 110.835, es siempre divisible por 9 (es sencillo justificar esto utilizando la representación decimal de los números), luego verifica la regla de divisibilidad. Como ha elegido el 1, la suma del resto es 1 + 0 + 8 + 3 + 5 = 17, y aplicando la regla de nuevo 1 + 7 = 8. Como falta 1 para llegar a 9, entonces, ese es el dígito elegido y oculto.

Las reglas de divisibilidad de los números 6 = 2 x 3, 12 = 3 x 4 y 15 = 3 x 5 son consecuencia inmediata de las reglas anteriores, por ejemplo, un número es divisible por 6 si es divisible por 2 y 3.
La regla de divisibilidad del 6: un número es divisible por 6 si, y sólo si, el dígito de las unidades es 2, 4, 6, 8 o 0, y la suma de sus dígitos es divisible por 3.
La regla de divisibilidad del 12: un número es divisible por 12 si, y sólo si, la suma de sus dígitos es divisible por 3 y el número formado por los dos dígitos de la derecha del número es divisible por 4.
La regla de divisibilidad del 15: un número es divisible por 15 si, y sólo si, el dígito de las unidades es 0 ó 5, y la suma de sus dígitos es divisible por 3.
Reglas de divisibilidad de 7, 11 y 13. Empecemos por la regla de divisibilidad del 11, que es la más sencilla de formular y de explicar.
La regla de divisibilidad del 11: un número es divisible por 11 si, y sólo si, la suma alternada de sus dígitos (es decir, se va alternando suma y resta) es múltiplo de 11 (incluido el 0).
Veamos algún ejemplo. Empecemos por el número con el que abríamos esta entrada, el 1.056.475.343. Calculemos la suma alternada de sus dígitos 1 – 0 + 5 – 6 + 4 – 7 + 5 – 3 + 4 – 3 = 0, luego es múltiplo de 11. Otro ejemplo sería el número 2.519, cuya suma alternada de sus dígitos es 2 – 5 + 1 – 9 = – 11, luego efectivamente el divisible por 11.
Ahora veamos la propiedad 2 enunciada al principio de esta entrada: Los números capicúas con un número par de dígitos son divisibles por 11.
En los números capicúas con una cantidad par de dígitos, como 327.723, los dígitos que ocupan posiciones impares y pares son los mismos, e igual a los dígitos que están en la derecha y la izquierda del número (posiciones impares desde la izquierda, 3, 7, 2, mientras que en las pares 2, 7, 3), luego la suma alternada es cero, por lo que se cumple la regla de divisibilidad del 11.
Veamos la razón por la que este criterio de divisibilidad funciona. Si tenemos un número N con n + 1 dígitos, N = an an–1 … a2 a1 a0, cuyo valor será entonces
![]()
tenemos que tener en cuenta que, como buscamos la multiplicidad con el número 11, se producen las siguientes igualdades de las potencias de 10,
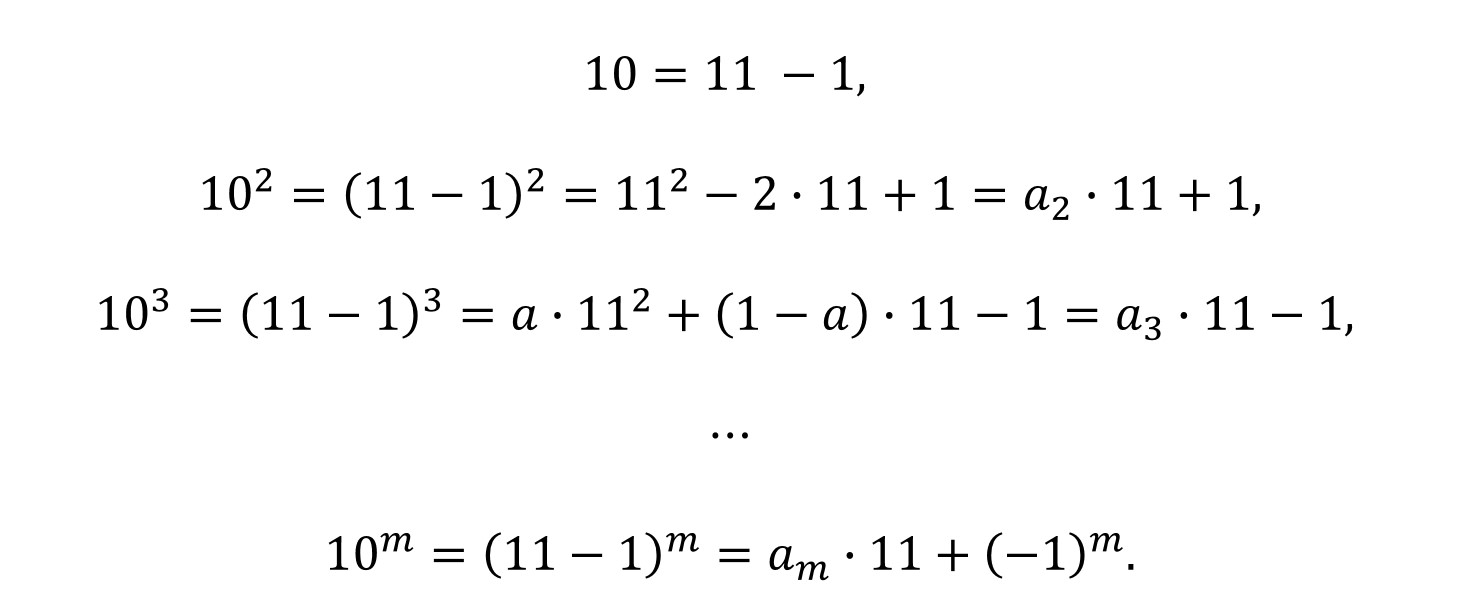
que llevadas a la formula anterior nos dicen que el número N es múltiplo de 11 si la suma alternada
![]()
es múltiplo de 11.

Terminemos este grupo expresando similares criterios de divisibilidad para los números 7, 11 y 13. Estos se pueden demostrar con un argumento similar al anterior, teniendo en cuenta el hecho de que 1001 = 7 x 11 x 13.
La regla de divisibilidad del 7, 11 y 13. Un número es divisible por 7, 11 o 13, respectivamente, si la suma alternada de los grupos de tres dígitos, empezando por la derecha, también lo es.
Por ejemplo, si tomamos la suma alternada de los grupos de tres dígitos del número 5.166.574.959 se obtiene 959 – 574 + 166 – 5 = 546. Como 546 es el producto de 6, 7 y 13, se deduce que el anterior número es divisible por 7 y 13, pero no por 11.

A lo largo de esta entrada del Cuaderno de Cultura Científica hemos visto los criterios de divisibilidad de los números de un dígito, es decir, de las cifras básicas de nuestro sistema de numeración, y de algún número más, como 11, 12, 13 o 15, por lo que estamos en condiciones de resolver el reto matemático de John H. Conway de “las diez divisibilidades”. Espero que os animéis a resolverlo por vuestra cuenta … la respuesta al mismo es 3.816.547.290, aunque lo interesante es el camino para llegar a ella, ¡que lo disfrutéis!
Bibliografía
1.- Alex Bellos, Did you solve it? John Horton Conway playful maths genius, The Guardian, 2020.
2.- Martin Gardner, The Unexpected Hanging and other Mathematical Diversions, University of Chicago Press, 1991.
3.- Peter M. Higgins, Number Story: From Counting to Cryptography, Springer-Verlag, 2008.
4.- Ellina Grigorieva, Methods of Solving Number Theory Problems, Birkhauser, 2018.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Las curiosas reglas de divisibilidad (II) — Cuaderno de Cultura Científica
[…] la anterior entrada del Cuaderno de Cultura Científica titulada Las curiosas reglas de divisibilidad presentamos algunos criterios de divisibilidad de los números de un solo dígito, es decir, de las […]
José Ocanto
Podría explicar detalladamente cómo pasa de 11² + 2.11 + 1 a a2.11 +1?
Juan Gordillo Lobato
Sacando 11 factor común de los dos primeros sumandos, creo
Juan Gordillo Lobato
Hay un método más cómodo y fácil de recordar, pero que no suele explicarse (no entiendo por qué).
Consiste en agrupar las cifras de dos en dos a partir de la derecha, e ir sumando los números de dos cifras así obtenidos. La suma es múltiplo de 11 sí y solo si el número inicial es múltiplo de 11.
En el ejemplo 1.056.475.343:
43+53+47+56+10=209; 2+09=11. Por tanto el número pedido es múltiplo de 11.
La demostración del criterio queda como ejercicio.
Un saludo, y muchas gracias