La imaginación de las personas es increíble. En anteriores entradas del Cuaderno de Cultura Científica, como Los números enamorados o ¿Pueden los números enamorarse de su propia imagen?, hemos visto curiosas e interesantes familias de números naturales, sin embargo, la imaginación matemática no deja de crear, o descubrir si uno cree en el platonismo matemático, fascinantes grupos de números. En esta entrada os hablaré de los números llamados harshad o de Niven.

Un número natural se dice que es un número harshad, o también, de Niven, si es divisible por la suma de sus dígitos. Por ejemplo, el número 18 es harshad porque es divisible por 1 + 8 = 9, como también lo es el número de la bestia, el 666 (véanse las entradas 666, el número de la bestia (1) y (2)), divisible por 6 + 6 + 6 = 18, o el número de Hardy-Ramanujan 1729 (véase la entrada Las matemáticas del taxi ), divisible por 1 + 7 + 2 + 9 = 19. Sin embargo, el 25 no es un número de Niven ya que no es divisible por 2 + 5 = 7, ni tampoco lo son todos los números primos con más de un dígito.

El concepto de número harshad fue introducido por el matemático recreativo indio Dattatreya Ramchandra Kaprekar (1905-1986), a quien le debemos algunos descubrimientos de teoría de números como la constante de Kaprekar, los números de Kaprekar, los autonúmeros o los números harshad, en su artículo Multidigital numbers, publicado en la revista Scripta Mathematica en 1955. El nombre harshad viene de la unión de las dos palabras del sánscrito “harsa”, que significa alegría o felicidad, y “da”, que significa “dar”, por lo que sería algo así como “que da, o proporciona, alegría”.

El concepto fue introducido de nuevo por el matemático canadiense-estadounidense Ivan M. Niven (1915-1999), que fue presidente de la Mathematical Association of America, en una charla que impartió en un congreso de teoría de números en 1977. Por este motivo, se les conoce también como números de Niven.

Una de las ventajas de una familia como esta es que es sencillo calcular por uno mismo, a mano o con calculadora, los primeros números de la misma, por ejemplo, los menores que 1.000, que se muestran más abajo, o hasta la cantidad que cada cual decida. Los números harshad se corresponden con la sucesión A005349 de la Enciclopedia online de sucesiones de números enteros, del matemático británico-estadounidense N. J. A. Sloane. Los menores de 1.000 son:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72, 80, 81, 84, 90, 100, 102, 108, 110, 111, 112, 114, 117, 120, 126, 132, 133, 135, 140, 144, 150, 152, 153, 156, 162, 171, 180, 190, 192, 195, 198, 200, 201, 204, 207, 209, 210, 216, 220, 222, 224, 225, 228, 230, 234, 240, 243, 247, 252, 261, 264, 266, 270, 280, 285, 288, 300, 306, 308, 312, 315, 320, 322, 324, 330, 333, 336, 342, 351, 360, 364, 370, 372, 375, 378, 392, 396, 399, 400, 402, 405, 407, 408, 410, 414, 420, 423, 432, 440, 441, 444, 448, 450, 460, 465, 468, 476, 480, 481, 486, 500, 504, 506, 510, 511, 512, 513, 516, 518, 522, 531, 540, 550, 552, 555, 558, 576, 588, 592, 594, 600, 603, 605, 612, 621, 624, 629, 630, 640, 644, 645, 648, 660, 666, 684, 690, 700, 702, 704, 711, 715, 720, 730, 732, 735, 736, 738, 756, 770, 774, 777, 780, 782, 792, 800, 801, 803, 804, 810, 820, 825, 828, 832, 840, 846, 864, 870, 874, 880, 882, 888, 900, 902, 910, 912, 915, 918, 935, 936, 954, 960, 966, 972, 990, 999, 1.000.

Como podemos observar hay muchos números de Niven entre los mil primeros números, en concreto, 213. Sin embargo, como demostraron en 1985 los matemáticos estadounidenses Robert E. Kennedy y Curtis N. Cooper la densidad de estos números es cero, es decir, que cuanto más grandes sean los números naturales considerados menos números que proporcionan alegría habrá. En otras palabras, si N(n) es la cantidad de números de Niven menores, o iguales, que n, entonces el límite del cociente N(n) / n es cero.

Una curiosidad de estos números está relacionada con los números factoriales. Recordemos que el factorial de un número m es el número igual a la multiplicación de todos los números naturales menores, o iguales, que el mismo, es decir, m! = m x (m – 1) x (m – 2) x … x 3 x 2 x 1. Así, para los primeros números naturales sus factoriales son 1! = 1, 2! = 2, 3! = 6, 4! =24, 5! = 120, 6! = 720, 7! = 5040, y podríamos continuar. Si nos fijamos, todos esos números son de Niven, incluso si continuamos con algunos más, 40.320, 362.880, 3.628.800, 39.916.800, … descubriremos que lo siguen siendo. Por este motivo, algunas personas interesadas en el estudio de esta familia se preguntaron si todos los números factoriales serían de los que proporcionan alegría. La respuesta es negativa, ya que la suma de los dígitos del factorial del número 432, es 3.897, cuya descomposición en factores primos es 3² x 433, pero el número primo 433 no puede dividir a 432!. En consecuencia, el factorial 432! no es harshad.

Otra propiedad que se ha estudiado ha sido la existencia de números harshad consecutivos, más allá de los diez primeros números. La primera pareja es, como puede verse arriba, 20 – 21, aunque hay muchas más, como 80 – 81. El primer trio de números de Niven es 110 – 111 – 112. Los cuatro primeros números consecutivos que producen alegría son 510 – 511 – 512 – 513. Mientras que para obtener cinco números consecutivos ya nos tenemos que desplazar a números más grandes, en concreto al sexteto que empieza en 131.052.

En 1982 el matemático Robert E. Kennedy demostró que no es posible construir una sucesión de 21 números harshad consecutivos, pero como probaría después con su colega Curtis Cooper, sí se pueden construir 20 números de Niven consecutivos, de hecho, existen infinitos ejemplos de tales sucesiones. Aunque la más pequeña de esas familias tiene más de 44.363.342.786 dígitos.

La propiedad definitoria de los números harshad está dada en función de los dígitos de la representación del número, luego no es una propiedad del número en sí mismo, sino que depende de la base de numeración en la que lo representemos.

Empecemos considerando el sistema binario, es decir, la representación de los números en base dos (véase por ejemplo el video de la serie Una de mates dedicado a los números binarios). Por ejemplo, los números 20, 21, 27 y 34 se representan en el sistema binario como:

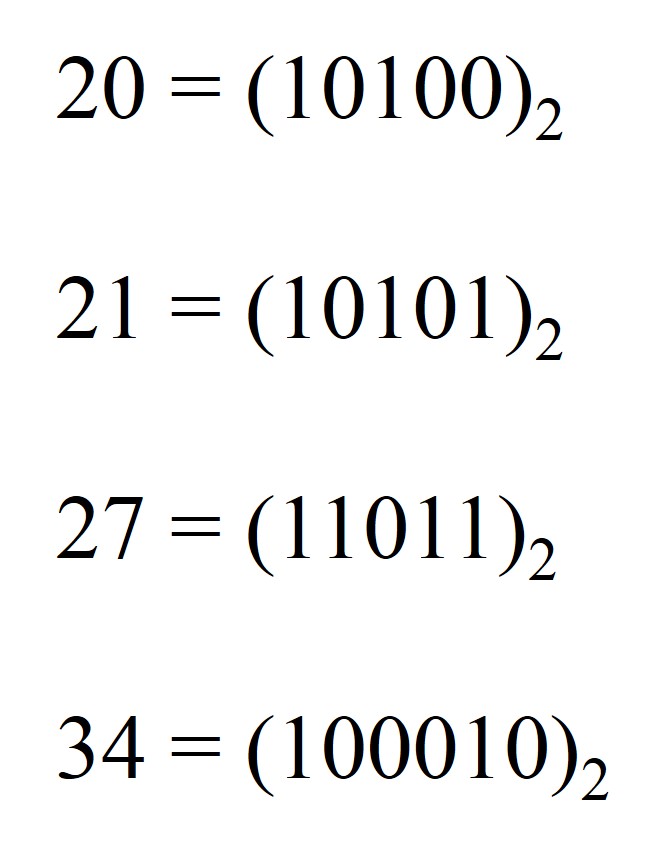
Recordemos que los unos y ceros de la representación binaria nos están diciendo qué potencias de 2 se utilizan para expresar el número como sumas de potencias de 2. Como los tres primeros números binarios anteriores tienen 5 dígitos las potencias de 2 implicadas son 16, 8, 4, 2 y 1. Además, 20 = 16 + 4 (16 sí, 8 no, 4 sí, 2 no y 1 no), 21 = 16 + 4 + 1 y 27 = 16 + 8 + 2 + 1. El último número tiene 6 dígitos, luego implica también a la potencia 32, de hecho, 34 = 32 + 2 (32 sí, 16 no, 8 no, 4 no, 2 sí y 1 no).

La suma de los dígitos binarios del número 20 es 2 (véase la imagen anterior), que divide a 20, luego el número 20 es un número 2-harshad (donde el prefijo indica en la base en la que tiene esa propiedad, luego en los casos normales, cuando no lo hemos indicado, habría sido 10-harshad). Y la suma de los dígitos binarios de 21 es 3, que divide a 21, luego también es 2-harshad. Por lo tanto, 20 y 21 son 2-harshad y 10-harshad.

Por otra parte, 27 que es 10-harshad, no es 2-harshad, ya que la suma de sus dígitos es 4, que no divide a 27. Mientras que para el 34, que no es 10-harshad, la suma de sus dígitos es 2, que divide a 34, luego sí es 2-harshad.

Al igual que hemos comentado antes para la base decimal, podríamos calcular los primeros números (hasta la cantidad que deseemos) que son harshad en la base binaria, es decir, que son 2-harshad. En general, podemos calcular los números b-harshad para cualquier base de numeración b, no solo 2 o 10.

Para un sistema de numeración en base b, los primeros b números naturales –que se corresponden con las b – 1 cifras básicas no nulas y el número de la base b, son trivialmente números b-harshad.

Los únicos números primos que pueden ser b-harshad son aquellos que son menores, o iguales, que la base. Por eso los únicos primos de Niven en la base decimal son 2, 3, 5 y 7, o el número 11 es 12-harshad.

Existen cuatro números que son b-harshad para cualquier base b, que son 1, 2, 4 y 6. Aunque el número 12 casi les acompaña, puesto que es b-harshad para todas las bases, excepto b = 8.

Pero volvamos a los números harshad, o de Niven, para la base decimal, aunque lo que vamos a comentar a continuación también sería válido para cualquier base. Vamos a considerar dos familias particulares dentro de esta familia. La primera es la formada por los números harshad (o de Niven) múltiples, que son aquellos tales que, al dividirlos por la suma de sus dígitos, el resultado es otro número harshad. Por ejemplo, el número 6.804, que al dividirlo por la suma de sus dígitos, 18, el resultado 378 sigue siendo un número que proporciona felicidad. Más aún, con este número se puede seguir el proceso, hasta un total de cuatro veces (llamada multiplicidad de número de harshad múltiple 6.804), como se muestra en la imagen.

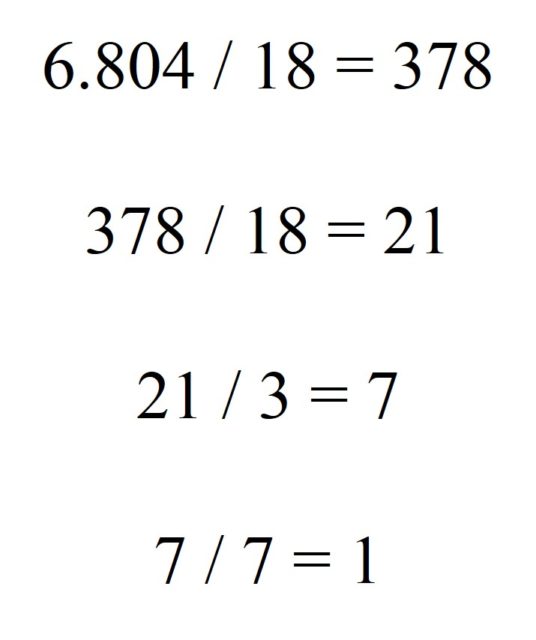
O el número 987.552, que es harshad múltiple, con multiplicidad 3, ya que en el proceso de dividir por las sumas de los dígitos se obtienen los números de Niven 27.432 y 1.524, pero el siguiente resultado 127 ya no lo es.

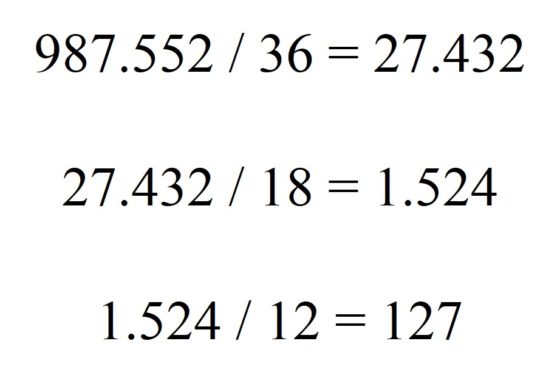
El número 2.016.502.858.579.884.466.176 harshad múltiple, con multiplicidad 12, como se muestra en la imagen, donde los divisores son las sumas de los dígitos de los números del dividendo, y los resultados se escriben en la línea siguiente.

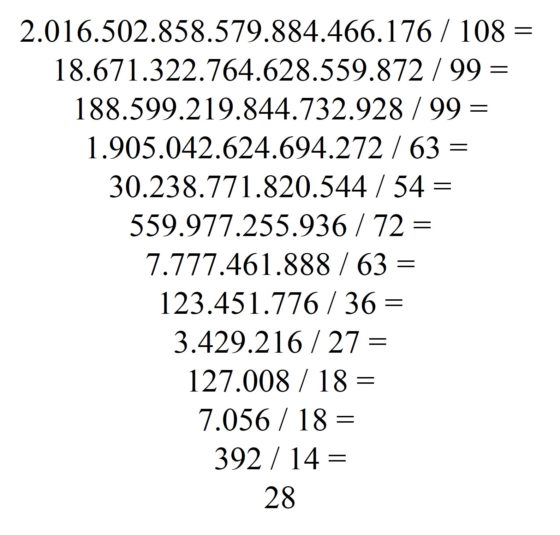
Una subfamilia interesante dentro de los números harshad podría la fromada por aquellos números tales que al dividirlos por la suma de sus dígitos el resultado sea el producto de los mismos. O lo que es equivalente, el número se puede escribir como el producto de la suma de sus dígitos por el producto de los mismos, por eso reciben el nombre de números suma-producto. Un ejemplo es el número 135 que, al dividirlo por la suma de sus dígitos, 1 + 3 + 5 = 9, el resultado es 15, que es el producto de los mismos. A pesar del interés de esta propiedad, realmente solo existen 3 números que cumplen la misma, 1, 135 y 144.

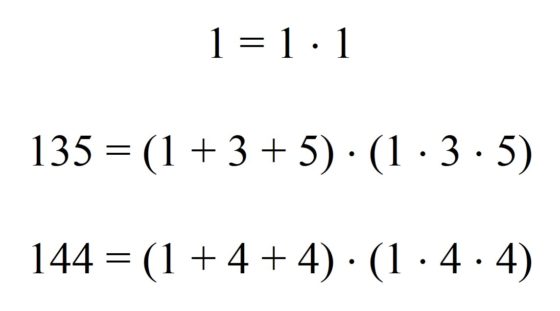
Para terminar esta entrada del Cuaderno de Cultura Científica introduciremos los números harshadmórficos, o Nivenmórficos, que son aquellos números n tales que existe un número harshad N cuya suma es el número n y además está en los últimos dígitos de N. Por ejemplo, el número 18 es harshadmórfico ya que existe el número de Niven 16.218, cuyos dígitos suman 18 y termina en 18.

El matemático Sandro Boscaro demostró que curiosamente todos los números, salvo el 11, son harshadmórficos. Siempre se puede encontrar un número de Niven que termine en ese número y sus dígitos también sumen el propio número.

Por ejemplo, si tomamos el número 12, por el resultado de Boscaro sabemos que es harshadmórfico. De hecho, la suma de los dígitos y la terminación del número de Niven 912 es 12. Lo cual vale para cualquier otro número, que no sea once. Os dejo como entretenimiento buscar los correspondientes números de Niven para los números menores que 30 (salvo 11, claro).

Bibliografía

1.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Press, 1998.

2.- J. Sándor, B. Crstici, Handbook of Number Theory II, Kluwer Academic Publishers, 2004.

3.- Wolfram MathWorld: Harshad Number

4.- Wikipedia: Harshad number

5.- N. J. A. Sloane, The On-line Encyclopedia of Integer Sequences: A005349

6.- D. R. Kaprekar, Multidigital numbers, Scripta Math. 21, 27, 1955.

7.- R. E. Kennedy, C. N. Cooper, On the natural density of the Niven numbers,

College Math. J. 15, no. 4, p. 309-312, 1984.

8.- R. E. Kennedy, Digital sums, Niven numbers and natural density, Crux Math. 8, p. 131-135, 1982.

9.- C. N. Cooper, R. E. Kennedy, On consecutive Niven numbers, Fib. Quart.

21, p. 146-151, 1993.

10.-Boscaro, Sandro, Nivenmorphic integers, Journal of Recreational Mathematics 28 (3), p. 201–205, 1996–1997.

11.- Página web del artista Nicky Broekhuysen

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica