Hace un año, con el inicio del período de las vacaciones estivales de los centros educativos, publicamos en el Cuaderno de Cultura Científica la entrada FUN WITH MATHS, diversión con matemáticas, en la que se explicaban algunos sencillos trucos de magia relacionados con las matemáticas. En esta entrada recuperamos esta idea y mostramos otros dos trucos de magia matemática con los números.


Vayamos con el primer truco. Es un sencillo truco en el que se pide a una persona del público que piense en un número de cuatro dígitos, que finalmente vamos a recuperar tras algunas operaciones aritméticas. Una parte muy importante de los trucos de magia es la presentación de los mismos, así como todo el teatro que se realiza en su puesta en escena. Por ejemplo, este truco se puede presentar de la siguiente forma.
La persona que realiza el truco dispone de una pizarra o una hoja de papel grande sobre la que realizará el truco. Para empezar, le pide a alguien del público que piense un número de cuatro dígitos y que lo diga en alto, para que todo el mundo lo escuche. La persona que realiza el truco, con cierta teatralidad, le dirá que ha elegido un número muy especial, con propiedades mágicas. A continuación, se explican cuáles son esas propiedades mágicas.
El mago, o la maga, escribirá en la pizarra, en grande, el número que ha elegido la persona voluntaria del público. Pensemos que ese número es 7.483.
Después, siempre con la mayor teatralidad posible, escribirá en la pizarra el primer dígito, desde la izquierda, del número: en nuestro ejemplo, 7.
Debajo de este, y con el objetivo de realizar una suma, escribirá el número formado por los dos primeros dígitos, desde la izquierda: en el ejemplo, 74.
Más abajo aún escribirá el número formado por los tres primeros dígitos: 748. Y sumará esos tres números. Para el número elegido el resultado es 7 + 74 + 748 = 829.
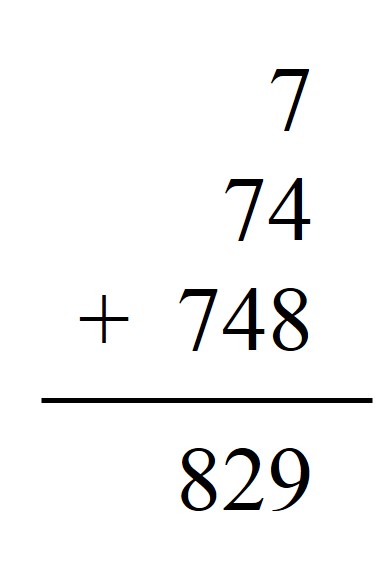
El siguiente paso es multiplicar en la pizarra el resultado de la operación anterior por 9. En el ejemplo elegido quedará 829 x 9 = 7.461.
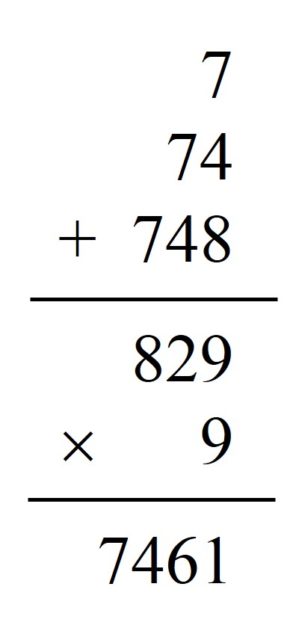
Finalmente, hay que sumar a ese resultado la suma de los dígitos del número elegido por la persona voluntaria, que en nuestro ejemplo es 7 + 4 + 8 + 3 = 22, y sorpresa, sorpresa, el resultado es efectivamente el número mágico en cuestión, 7.461 + 22 = 7.483.
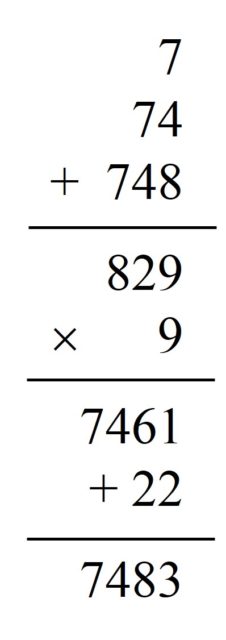
Se puede comprobar fácilmente que este truco funciona siempre. Dado un número de cuatro dígitos abcd, la operación mostrada en el truco, que es (a + ab + abc) x 9 + (a + b + c + d) da como resultado abcd.
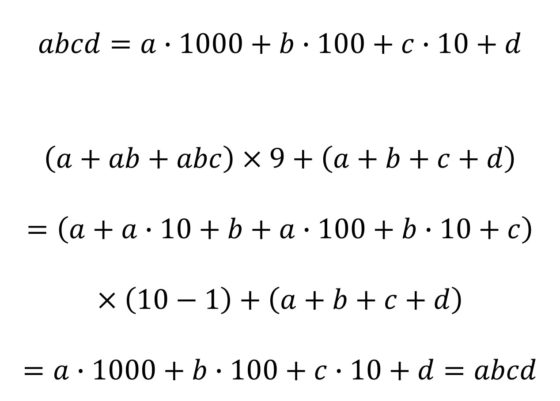
Si se realiza con detalle la operación anterior podemos darnos cuenta de por qué funciona el truco y, además, de que funcionará con un número con cualquier cantidad de dígitos.
Es un truco que no se puede hacer dos veces seguidas, al menos presentado así, ya que el público descubriría que todos los números son especiales. Lo mejor es hacerlo una vez y luego hacer otro sencillo truco, por ejemplo, el truco de la calculadora que expliqué en el video de la sección Una de mates, de la Cátedra de Cultura Científica, y que fue emitido en el programa de humor y ciencia de televisión, dirigido por José A. Pérez Ledo, Orbita Laika (segunda temporada) de La2, de Televisión Española: Una de mates, magia matemática.

El segundo truco es un truco de cálculo mental que se puede presentar como una competición entre la mente del mago y la calculadora. Para realizar el truco se necesita una pizarra, o una hoja de papel, grande que puedan ver todas las personas del público, y una calculadora de las básicas.

Se explica que va a ser una competición entre la mente del mago y la calculadora, por lo que se necesita una persona voluntaria para que realice las operaciones en la calculadora, intentando hacerlo rápido y ganar al cálculo mental. Además, se le dará papel y lápiz por si necesita apuntar algo. Se le pide a otra persona del público que piense, y diga en alto, un número de cuatro dígitos (llamémosle en la explicación A), que se escribirá en la pizarra como se muestra más adelante en la imagen.
Para el cálculo que se va a realizar se necesita un segundo número, también de cuatro dígitos, para multiplicar por el primero, pero si solo fuese eso sería muy simple y efectivamente fácil que ganara la calculadora, por lo que vamos a complicar un poco la operación aritmética. ¿Cómo? Otra persona del público dará ese segundo número de cuatro dígitos (llamémosle B para la explicación) y la persona que realiza el truco un tercer número de cuatro dígitos (denotémoslo C). La competición consiste en multiplicar el primer número (A) por cada uno de los otros dos (A x B y A x C) y sumar el resultado (A x B + A x C). Para explicarlo mejor al público y realizar el truco se pinta el siguiente diagrama en la pizarra, suponiendo que el primer número A ofrecido por el público sea 7.354.
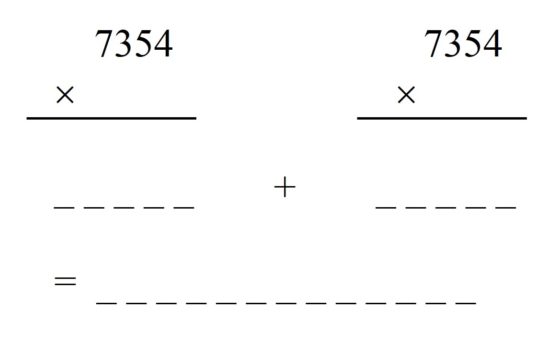
Debajo del 7.354, a la izquierda, se escribirá el segundo número proporcionado por quienes están presentes en el espectáculo de magia matemática, mientras que debajo del 7.354, a la derecha, se escribirá el número que aporta la maga matemática. Y en ese momento empieza la competición. Repetimos, se trata de ver quién consigue antes el resultado de multiplicar ese primer número 7.354 por cada uno de los dos anteriores y sumar esos resultados parciales.
Expliquemos con un ejemplo el desarrollo del truco de magia matemática. Supongamos que la segunda persona del público sugiere el número 4.067, entonces la persona que hace el truco deberá aportar el tercer número, que debe parecer que es uno cualquiera que se le ocurre en ese momento, pero que realmente cada uno de sus dígitos es el complementario respecto a 9 del dígito correspondiente del segundo número. Por lo tanto, en el ejemplo, como el segundo número es 4.067, el número que aportará el mago será 5.932 (4 + 5 = 9, 0 + 9 = 9, 6 + 3 = 9 y 7 + 2 = 9).
Es decir, con estos números concretos la competición consiste en realizar las multiplicaciones del primer número por cada uno de los otros dos, 7.354 x 4.067 y 7.354 x 5.932, y sumar los resultados de las mismas, es decir, (7.354 x 4.067) + (7.354 x 5.932).
El mago, que realiza el cálculo mental, escribirá rápidamente la solución en la parte de debajo de la pizarra, que es 73.532.646 (más adelante explicaremos de dónde ha sacado el mago ese número). La persona de la calculadora y el público se quedarán sorprendidos de la rapidez del mago, ya que habrá sido imposible realizar la operación con la calculadora en tan corto plazo de tiempo. Entonces, con ayuda de quien tiene la calculadora, se escribirán en la pizarra los pasos intermedios y el resultado final, como se muestra en la siguiente imagen, para comprobar que el número escrito es el correcto.

Expliquemos cómo ha conseguido el mago ese número y por qué sabe que es la solución buscada. Los cuatro primeros dígitos consisten en el primer número proporcionado por el público menos 1, es decir, 7354 – 1 = 7353. Mientras que los cuatro siguientes dígitos son los complementos respecto a 9 de cada uno de los dígitos de este, esto es, 2646. Juntando todo, y poniendo los puntos correspondientes, 73.532.646.
El motivo es el siguiente. Si llamamos a los tres números proporcionados A, B y C como se indicaba más arriba, el resultado que se busca es:
![]()
Pero por la propiedad distributiva, eso es lo mismo que:
![]()
Aquí está la clave del truco de magia. Como la persona que realiza el truco puede elegir C esto le permite controlar el valor de B + C y simplificar la operación aritmética. Veamos un ejemplo sencillo. Si se elige C de forma que B + C = 10.000, entonces A x (B + C) es el primer número elegido seguido de cuatro ceros, en nuestro ejemplo, 73.540.000. Pero de esta forma las personas presentes se darían cuenta de cómo has realizado el truco. Es decir, hay que esconder el truco y que parezca realmente una operación aritmética complicada.
Por este motivo se elige C para que B + C = 9.999, es decir, los complementos dígito a dígito respecto de 9 del número B. Y la operación se transforma en A x 9.999, que como es A x (10.000 – 1), el resultado es el número A menos 1 seguido de su complemento dígito a dígito respecto de nueve. En el ejemplo, 7353 y 2646, que puesto junto y poniendo los puntos de los miles (esto esconde un poco de donde viene el número, por lo que es aconsejable poner los puntos) es 73.532.646.
Bueno, pues ya conocéis otro par de trucos de magia para amenizar las reuniones familiares o con amigos. Espero que os hayan gustado.


Bibliografía
1.- Peter McOwan, Matt Parker, The manual of Mathematical Magic.
2.- Pedro Alegría, El rincón matemático (DivulgaMAT)
3.- Pedro Alegría, MAGIA por principios, Publidisa, 2008.
4.- Fernando Blasco, Matemagia, Temas de Hoy, 2007.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Justo Fernández
Excelente artículo Raúl. Pondré en práctica los juegos de matemagia en clase, me parecen muy interesantes.
Me encanta la matemática recreativa y me gustaría aportar este artículo https://soymatematicas.com/matematicas-recreativas/ para los lectores.
Todo lo que sea hacer pensar y tocar las matemáticas a los alumnos siempre es positivo para su aprendizaje.
Saludos. Gracias
RAUL IBAÑEZ TORRES
Muchísimas gracias Justo,
Existen muchas herramientas interesantes para el aprendizaje de las matemáticas. La matemática recreativa es una buena herramienta, además de un buen camino para acercarse a las matemáticas, como ya nos enseñó Martin Gardner, entre otros.
Un fuerte abrazo, Raúl