Javier Duoandikoetxea
Las huellas dactilares nos identifican, por eso los detectives las buscan en el lugar donde se ha producido un delito. No resulta sorprendente, por tanto, saber que hay colecciones gigantescas de huellas dactilares en los archivos policiales.

El FBI comenzó a tomar huellas dactilares en 1924 mediante el uso de fichas de cartón, en las que los dedos mojados en tinta dejaban su marca. En 1993, ya tenía almacenadas más de 25 millones de fichas. Para entonces, el uso de los ordenadores ya había comenzado a extenderse y estaba claro que los archivos digitales reportarían grandes ventajas, tanto para guardar huellas dactilares como para realizar búsquedas, por lo que se procedió a la digitalización.
Es importante asegurar con la mayor precisión posible a quién pertenece una huella dactilar. Por eso, para digitalizar los archivos se eligió una imagen de 500 puntos por pulgada, a escala de colores grises de 8 bytes. Esto generaba un fichero de 10 MB de cada ficha, de modo que la digitalización de todo el archivo requería soportes con gran espacio. Además, hace 25 años la capacidad de almacenamiento de los dispositivos era muy inferior a la actual. Entonces, ¿qué hacer? La clave estaba en la compresión.
Recordemos que comprimir es reducir el tamaño del fichero y que, para que eso resulte útil, hay que hacerlo sin perder información importante. El sistema de compresión JPEG, habitual para las fotografías, se lanzó en 1992 y fue el elegido por los expertos del FBI para llevar a cabo el proceso de digitalización. A pesar de ello, no quedaron satisfechos con los resultados, ya que la imagen resultante no les parecía adecuada. ¿Por qué?
En la mayoría de los casos, al pasar de un píxel a otro el cambio de color que se produce es pequeño, que es lo que aprovecha el sistema JPEG. Por eso, en las zonas de los bordes el resultado no es tan bueno, ya que se pueden producir cambios de color importantes en los píxeles de alrededor. Se puede decir, en cierta medida, que en las imágenes de las huellas dactilares lo único que tiene importancia son los bordes (rayas).
Para resolver el problema, investigadores de varias universidades y agencias gubernamentales de Estados Unidos colaboraron en la búsqueda de un buen algoritmo adaptado a la compresión de imágenes de huellas dactilares.
Intervalo matemático
En 1984, el matemático francés Yves Meyer trabajaba como profesor en la Universidad de París-Orsay cuando un compañero físico le enseñó un artículo, pensando que sería de su interés. Los autores eran Jean Morlet y Alex Grossmann, ingeniero geofísico de la empresa Elf Aquitaine el primero y físico de la Universidad de Marsella el segundo.

El artículo proponía una nueva vía de detección de gas y petróleo. Para detectar el petróleo y las bolsas de gas subterráneas, se emite una onda y, mediante el análisis de la señal que regresa tras atravesar varias capas, se obtiene información sobre la composición interna. Morlet presentó una nueva técnica para hacerlo y trabajó el campo matemático con Grossmann, pero no tuvo mucho éxito en la empresa y, según dicen, únicamente consiguió una jubilación anticipada. Sin embargo, la fama le llegó del mundo de la ciencia.
Yves Meyer se quedó sorprendido por lo que vio en el artículo: en él se encontró con fórmulas conocidas, de un campo que dominaba perfectamente, y consideró que podía ser un camino fructífero entablar relación con los autores. Según cuenta él mismo, tomó el tren para Marsella en busca de Grossmann. En pocos años, Meyer y sus colegas y discípulos convirtieron aquellos torpes pasos iniciales en una teoría matemática.
Los componentes básicos para desarrollar una función en la teoría clásica de Fourier son las funciones trigonométricas. En la nueva teoría, estos componentes básicos cambian y se utilizan dilataciones y traslaciones de una función madre. Eso sí, esa madre necesita propiedades adecuadas para ser de utilidad. De todas formas, hay muchas opciones y se puede decidir la más apropiada en función del uso, lo cual ya es, en sí mismo, una ventaja en las aplicaciones.
Morlet le puso un nombre francés al nuevo objeto: ondelette. Posteriormente, cuando el término llegó al inglés, se convirtió en wavelet, que es la denominación con la que ha recorrido el mundo científico. Aunque muchos usuarios utilizan el préstamo tal cual (wavelet), existen términos adaptados a cada idioma: ondícula (esp.), ondeta (cat.), onduleta (port.), por ejemplo.

El análisis tradicional de Fourier no detecta bien los grandes cambios de una función que se producen en un intervalo reducido, porque las funciones trigonométricas que utiliza como componentes no están localizadas. Las ondículas, en cambio, se localizan y se adaptan mejor para estudiar cambios drásticos de funciones. Además, conviene elegir la ondícula madre adecuada según el uso que le vayamos a dar. Esto puede tener un coste matemático mayor y, si es para aplicarlo, quizás también un coste económico, pero hará mejor el trabajo que queremos o necesitamos.
Sistemas de compresión WSQ y JPEG2000
La teoría de las ondículas, a diferencia de la teoría de las series de Fourier que le precedió, ha abordado al mismo tiempo el campo puramente matemático y las aplicaciones. Se comenzó a utilizar inmediatamente para el procesamiento de las señales y las técnicas habituales se adaptaron al nuevo campo. El salto de aquellos primeros pasos al mundo real no se hizo esperar. Es más, las aplicaciones han alimentado la propia teoría matemática, lanzando nuevos problemas.
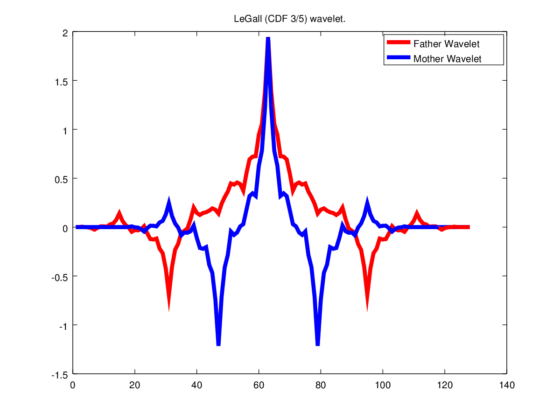
El sistema de compresión WSQ (Wavelet Scalar Quantization) para las necesidades del FBI se inventó con ayuda de ondículas. Además, lo pusieron a disposición de todo el mundo, libre. Este sistema usa matemáticamente una pareja de wavelets madre, una para la descomposición y la segunda para la reconstrucción de la imagen. Básicamente, siempre se hace lo mismo para la compresión: proporcionar la información que queremos guardar mediante una receta de componentes básicos (en este caso, wavelets) y hacer 0 los coeficientes de componentes de menor relevancia. Así, en la información que se va a almacenar se obtienen muchos ceros; se han ideado medios para guardar de forma breve esas listas de ceros.
Sin embargo, el uso de las ondículas para la compresión no quedó ahí. El mismo grupo que inventó el JPEG para las fotografías, creó otro estándar a través de wavelets: JPEG2000. Este modelo también se utiliza en la compresión de huellas dactilares cuando se toman imágenes de 1000 puntos por pulgada, pero no solo para eso: JPEG2000 se utiliza tanto en el cine digital, como en las imágenes que toman los satélites o en el protocolo DICOM de imágenes médicas.
Fourier moderno vs. Fourier clásico
El análisis de Fourier se enmarcó en el campo de las matemáticas teóricas a lo largo del siglo XIX y principios del XX. Sin embargo, posteriormente, se descubrieron multitud de campos en los que podía aplicarse en el mundo real, y con el aumento de la capacidad de cálculo de los ordenadores, se ampliaron aún más las posibilidades: señales, sonidos, imágenes médicas, espectrometría, cristalografía, telecomunicaciones, astronomía, visión artificial, reconocimiento de voz, etc.
La teoría de las ondículas, el nuevo campo que hemos visto crear y desarrollar, ha dado un nuevo impulso a estas aplicaciones. En el caso mencionado, el de las huellas dactilares, ofrece mejores resultados que la vía clásica, pero cabe preguntarse ¿merecerá la pena utilizar siempre las wavelets en lugar de las funciones trigonométricas? No, decidiremos en función de lo que queramos hacer. Por ejemplo, en nuestras cámaras fotográficas utilizamos JPEG porque no merece la pena recurrir a otro sistema de compresión para hacer fotos normales. La nueva teoría complementa la anterior, no la sustituye.
En 2017 el matemático Yves Meyer fue galardonado con el mayor premio que existe actualmente en matemáticas, el Premio Abel, «por su trabajo fundamental en el desarrollo de la teoría matemática de las ondículas«. Y en 2020 Yves Meyer, Ingrid Daubechies, Terence Tao y Emmanuel Candès han sido premiados con el Premio Princesa de Asturias de Investigación Científica y Técnica 2020, «por sus contribuciones pioneras y trascendentales a las teorías y técnicas matemáticas para el procesamiento de datos, que han ampliado extraordinariamente la capacidad de observación de nuestros sentidos y son base y soporte de la moderna era digital».
Para saber más:
En la red se puede encontrar más información sobre el tema. Estas son algunas de las fuentes que se pueden consultar:
- C. M. Brislawn, C.M. (1995). Fingerprints go digital. Notices of the American Matematical Society, 42 (11), 1278-1283.
- Web Mathouriste: Après Fourier, c’est encore du Fourier! (Hay abundante información sobre el análisis de Fourier, histórica en particular, en varias páginas del sitio web.)
- Web The Abel Przie: The Abel Prize Laureate 2017 – Yves Meyer.
Sobre el autor: Javier Duoandikoetxea es catedrático jubilado de Análisis Matemático en la UPV/EHU.
Este artículo se publicó originalmente en euskara el 19 de junio de 2019 en el blog Zientzia Kaiera. Artículo original.
Pablo Rodríguez
Una puntualización histórica: el análisis de Fourier, lejos de enmarcarse «en el campo de las matemáticas teóricas», tuvo aplicaciones directas a problemas de física, química e ingeniería desde su mismo nacimiento. De hecho, las series de Fourier se introducen por vez primera en Théorie analytique de la chaleur (Fourier, 1822), un libro sobre propagación del calor.
Pocas ramas del conocimiento se han beneficiado más de esta interacción entre matemáticas y física, entre lo teórico y lo aplicado. De esa interacción nacieron conceptos como la transformada de Fourier (nacida del problema práctico de analizar funciones no periódicas con series de Fourier) o la teoría de funciones ortogonales (nacida del problema práctico de resolver ecuaciones en derivadas parciales en dominios no rectangulares).