En la primera entrega de la serie Arte Moebius (I) en el Cuaderno de Cultura Científica, después de explicar brevemente qué es una banda de Moebius, algunas de sus curiosas características –que posee una sola cara y un solo borde– y un pequeño experimento para realizar en casa, habíamos dedicado la entrada a mostrar unos cuantos ejemplos de esculturas basadas en esta curiosa superficie. Los artistas mencionados en dicha entrada fueron Max Bill, José Ramón Anda, John Robinson, Jeremy Guy, Vladimir Vasiltsov y Eleonora Zharenova, A. Z. Nalich, Ernst Neizvestny, Mariko Mori y Chambliss Giobbi.

En la presente entrada vamos a seguir realizando un recorrido por algunas interesantes, curiosas y hermosas esculturas inspiradas en la superficie de una sola cara y un solo borde.

Para empezar, vamos a reiniciar este paseo artístico matemático con el mismo escultor con el que terminamos la entrada anterior, el estadounidense Chambliss Giobbi (Nueva York, 1963). Este artista neoyorkino trabaja con diferentes perspectivas sobre la banda de Moebius en una serie de esculturas, que son móviles, en las que utiliza coches de juguete para crear collages tridimensionales.

En su escultura Circunvalación de Moebius (2012), que mostramos en la entrada Arte Moebius (I), la estructura que subyace es un prisma cuadrado “flexible” rotado media vuelta y pegado por los extremos generando una doble banda de Moebius, además colocado para formar el símbolo del infinito (la curva llamada Lemniscata de Bernoulli). En su escultura Hoja de trébol de Moebius (2013) la forma que tiene la escultura es un nudo de trébol. Y finalmente la escultura móvil Rampa de salida de Moebius (2012), que podéis admirar más abajo y que me recuerda a otro de los curiosos experimentos relacionados con esta superficie.

Veamos el mencionado experimento. Para realizar este necesitamos únicamente una hoja de papel, de hecho, nos vale con una tira alargada con la que construir una banda de Moebius, un poco de cinta aislante para pegar los extremos de la cinta de papel y unas tijeras. Mientras que en la anterior entrada habíamos explicado lo que ocurría en una cinta normal y en una de Moebius cuando se cortan longitudinalmente las bandas por la mitad, ahora veremos qué ocurre si cortamos longitudinalmente las bandas, pero por una tercera parte de su anchura (véase el artículo de Marta Macho, Listing, Möbius y su banda ).

Cuando cortamos longitudinalmente una banda normal por un tercio de su altura el resultado son dos bandas normales, de la misma largura, pero anchuras distintas, una un tercio y otra dos tercios de la anchura original. Mientras que en el caso de una banda de Moebius el resultado son una banda de Moebius, igual de largo y con una anchura de un tercio de la original, y una banda normal retorcida, con el doble de largo y un tercio de ancho, ambas entrelazadas.

La escultura de Giobbi nos recuerda a este experimento, pero el escultor de Nueva York habría intercambiado las larguras, en la anterior escultura la banda de Moebius con coches de juguete tiene el doble de largura que la banda normal, y es mucho más ancha.

El siguiente escultor que quiero que nos encontremos en este paseo es el artista británico Richard Fox (1965) que, como muchos otros escultores interesados en la superficie de Moebius, trabaja tanto con la banda de una cara, como con la de dos caras. Richard Fox tiene dos series de esculturas, realizadas en bronce una y en mármol blanco otra, tituladas Moebius, una de las cuales vemos en la siguiente imagen.

Pueden verse más obras de la serie en la página web de Richard Fox. Así mismo, tiene dos series de obras tituladas Ravel (enmarañar o enredar), que son bandas normales con dos caras. En una de las series, White Ravel, cada una de las caras con un color diferente, blanco y arena.

Para la exposición OneOak/Unroble, que tuvo lugar en el Real Jardín Botánico de Edimburgo en 2012, Richard Fox realizó una banda de Moebius anudada, como un nudo de trébol, en madera de roble.

Otro artista que trabaja con la superficie de Moebius, así como con otras superficies geométricas y nudos “topológicos” es el escultor californiano T Barney, del que podéis admirar sus hermosas esculturas en la página T Barney Sculptures. Vamos a mostrar aquí dos ejemplos realizados en distintos materiales, piedra y bronce.

La primera escultura es Siringa (ninfa mitológica de Arcadia), realizada en piedra, en concreto, en arenisca de Arizona.

Podéis disfrutar de un video en el que se ve la escultura en movimiento, con algunos detalles de la misma, en particular, puede observarse el parecido de este material, arenisca de Arizona, con la madera, con la cual en ocasiones se confunde.

La siguiente escultura es Tisbe (figura femenina de la mitología griega), realizada en bronce con una pátina de jade (en la siguiente imagen), rubí, zafiro o turquesa.

Ypodéis disfrutar de un video en el que se ve la escultura en movimiento, con algunos detalles de la misma.

En el año 2000 celebramos en Bilbao el Congreso Internacional de Geometría Diferencial en memoria de Alfred Gray, dedicado al matemático estadounidense Alfred Gray (1939-1998) que había fallecido en otoño de 1998 durante una estancia de investigación en la Universidad del País Vasco/Euskal Herriko Unibertsitatea. Uno de los invitados del congreso fue el escultor Helaman Ferguson, amigo de Alfred Gray, con quien este había colaborado para la realización de una serie de esculturas sobre la superficie minimal de Costa. Por este motivo, Helaman Ferguson realizó para el congreso una escultura con la superficie de Costa, The Alfred Gray Memorial Bronze D4, K < 0 (2000).

Pero la pieza más conocida de este escultor es Umbilic Torus / Toro umbilical (1988), que es una obra relacionada con la banda de Moebius. Expliquemos la estructura de la misma.

Recordemos que para construir una banda de Moebius tomamos una tira plana (de papel), giramos media vuelta uno de los extremos y lo pegamos al otro extremo. Imaginemos ahora que disponemos de un prisma triangular, largo y flexible (para poder manipularlo, aunque sea en nuestra imaginación), que giramos 120 grados, es decir, un tercio de vuelta, uno de los extremos y lo pegamos al otro extremo –triángulo extremo contra triángulo extremo-, entonces tendremos una figura geométrica que solamente tiene una cara. Esto se debe a que cada cara del prisma se continúa con la siguiente donde se juntan los extremos, tras el giro de 120 grados. Esta es la figura con la que trabajaba también el escultor británico John Robinson en su obra Eternidad (1980) y que vimos en la entrada anterior, Arte Moebius (I).

Para la escultura Toro umbilical, Ferguson utiliza no un prisma triangular, sino un prisma de deltoide, una curva de tipo triangular. A continuación, se muestra una ilustración de la curva conocida como deltoide (que realmente es la trayectoria de un punto de una circunferencia que rueda, sin deslizarse, dentro de otra circunferencia más grande, de tres veces su radio) y otra de la figura geométrica generada con el prisma de deltoide.

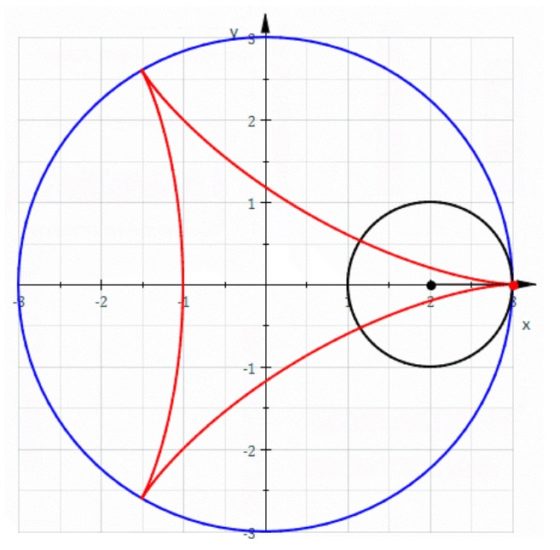
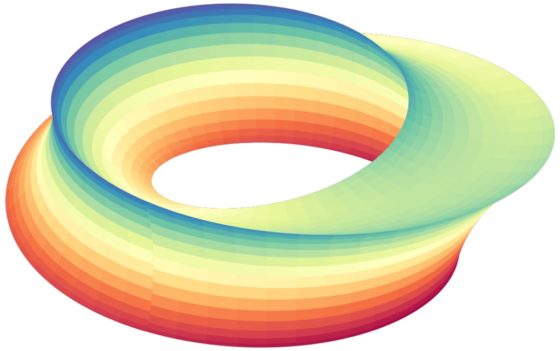
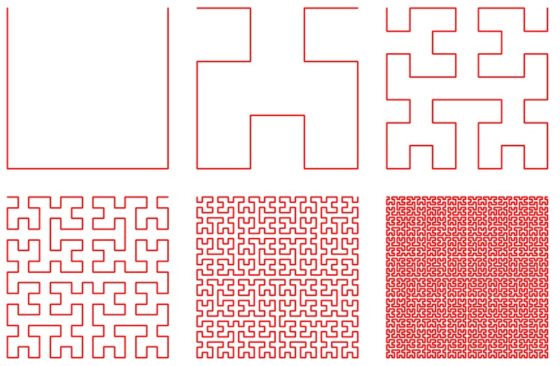
Finalmente, la superficie de la escultura no es lisa, sino que Helaman Ferguson ha añadido la forma de la curva fractal de Hilbert, que es una “curva que rellena el plano” (aunque en esta entrada no entraremos en las cuestiones matemáticas de esta curva fractal; puede verse su construcción en la entrada Fractus, arte y matemáticas). Esta curva se define por un proceso iterativo infinito y el escultor incluye una de las primeras iteraciones para que la curva sea visible.

Finalmente, el resultado del trabajo de Helaman Ferguson fue la escultura Toro umbilical (1988), que podemos ver aquí.

En la página web de Helaman Ferguson podéis ver una versión que realizó en 2012 del Toro Umbilical, en bronce, de 8,5 metros de altura, y que está en el exterior del Centro Simons de Geometría y Física de la Universidad Stony Brook.

A continuación, me gustaría hablar de dos escultores muy interesantes y que utilizan la banda de Moebius de una forma muy particular, representando en la escultura el espacio alrededor de este objeto geométrico, en lugar de la propia superficie. Son el artista estadounidense John Ernest (1922-1994) y el artista japonés Keizo Ushio.

Keizo Ushio (Fukusaki, Prefectura de Hyogo, 1951) es un artista con una obra escultórica muy geométrica, que al igual que algunos otros artistas mencionados en este paseo, ha llamado fuertemente la atención de la comunidad matemática.

Conocí a Keizo Ushio en el International Congress of Mathematicians que organizamos en Madrid en agosto de 2006, cuando le invitamos a realizar una escultura en vivo en el exterior del Palacio Municipal de Congresos de Madrid.

En la escultura Möbius in Space (2005) de Keizo Ushio, que mostramos más abajo, y en otras obras similares, el objetivo del artista no es representar la superficie de una sola cara y un solo borde, sino el espacio exterior que rodea a la misma. De manera que la cinta de Moebius es el “espacio vacío” en la escultura. El problema de esta idea es hacer visible esa superficie que no está y que está dentro de ese “espacio exterior”. Para ello, Keizo Ushio trabaja con el objeto geométrico tridimensional conocido en matemáticas como toro sólido. El toro es la superficie generada por una circunferencia que gira alrededor de un eje en el mismo plano de la circunferencia, y que esencialmente es la forma de un flotador, de manera que el toro sólido es el objeto tridimensional cuyo exterior es el toro, por lo que es como un donut.

El toro sólido va a jugar el papel de “espacio exterior” de la banda de Moebius, por lo tanto, tenemos que pensar en la banda de Moebius dentro del toro sólido.

Para entenderlo mejor, pensemos primero en la banda normal dentro del toro. Si consideramos todos los diámetros verticales de las circunferencias que rotadas forman el toro, estos segmentos forman una banda normal (dos caras y dos bordes), cuya anchura es el diámetro de esas pequeñas circunferencias del toro. ¿Cómo se obtendrá la banda de Moebius? Si consideramos primero un diámetro vertical y luego para las demás circunferencias del toro se van considerando los diámetros que van girando, desde ese vertical, de forma que al llegar al lugar de partida han dado medio giro, luego de nuevo es el diámetro vertical, esos segmentos forman una banda de Moebius dentro del toro. Pensemos que los segmentos representados en la siguiente imagen son los diámetros, que han girado media vuelta, de las circunferencias del toro, luego efectivamente es una banda de Moebius dentro del toro.

¿Cómo realiza Keizo Ushio este tipo de esculturas? Empieza con un bloque rectangular –con forma de paralelepípedo- de granito (suele trabajar con diferentes tipos de granito), que moldea con un martillo neumático hasta conseguir dejarlo con la forma de un toro sólido. Una vez conseguido el toro se trata de barrenar con el martillo neumático los diámetros que corresponden a la banda de Moebius.

Antes de continuar, veamos con un experimento casero qué pasaría en el caso de barrenar una banda normal dentro del toro sólido, como la descrita anteriormente. Para ello hemos cogido un donut (toro sólido), luego con un palillo chino (la barrena) hemos barrenado el donut (toro), pero con los diámetros verticales, creando un espacio vacío en el toro que es el vacío de “la banda normal”, que como tiene dos caras deja al exterior, el donut, con dos partes, la de fuera y la de dentro.

En el caso de la escultura Möbius in Space (2005) se barrenan los diámetros dando media vuelta, es decir, formando el vacío de la banda de Moebius, que como solo tiene una cara, el espacio exterior no puede dividirse en dos partes y es una sola pieza. En la siguiente ilustración, del profesor estadounidense de Ciencias de la Computación Carlo H. Séquin (véase Sculpture Designs by Carlo Sequin Inspired by Keizo Ushio), vemos un diagrama de esta idea.

El resultado de todas las ideas anteriores, es la escultura de Keizo Ushio, Möbius in Space (2005). En este caso, como el artista ha pintado el borde del espacio vacío, el impacto visual de la escultura es mayor.

¿Qué es lo que ocurriría en la anterior construcción si en lugar de barrenar los diámetros del toro girando media vuelta, lo hiciera ggirando una vuelta entera? Entonces tendríamos una banda normal –dos caras y dos bordes- retorcida. Por este motivo, en las esculturas de Keizo Ushio en las que barrena los diámetros del toro girados una vuelta entera la zona vacía es una banda normal retorcida, con dos caras, luego la escultura se separa en dos partes. Esto es lo que ocurre por ejemplo en la escultura Oushi-Zokei ICM Madrid 2006. Muchas personas relacionan esta escultura con la banda de Moebius, pero realmente es una banda normal retorcida, por eso se separa en dos partes.

La siguiente escultura, Dream Lens (2003), está realizada barrenando diámetros en el toro girando vuelta y media, desde el primero hasta volver al mismo, de forma que la parte vacía del toro es una banda de Moebius retorcida.

Aunque podríamos hablar muchísimo más de la obra de este genial escultor japonés, vamos a terminar con una serie de esculturas en las cuales tanto el espacio exterior, como el espacio vacío, son bandas de Moebius. Una de las piezas de esta serie es la escultura Möebius in space (1990), que mostramos a continuación.

La escultura Banda de Moebius (1971-72), del artista constructivista abstracto británico John Ernest (1922-1994) está basada en una idea similar a la de la escultura Möbius in Space (2005) de Keizo Ushio, aunque con un tratamiento más rectilíneo. El espacio exterior es un paralelepípedo con un “agujero” en medio, de manera que es “topológicamente” como un toro sólido. El espacio vacío es una banda de Moebius, pero colocada de forma más rectilínea dentro del espacio en el que está, con el objetivo de que en la imagen global, de frente, veamos un cuadrado dentro de otro cuadrado. El resultado es una pieza impactante.

Volvamos a las representaciones de la propia banda de Moebius, pero en esta ocasión se trata de una escultura curiosa y colaborativa. La siguiente artista utiliza el material reciclado para crear sus obras de arte, es la artista valenciana Rosa Montesa. Como la propia artista explica en su página web, sobre esta escultura:

Esta escultura es un encargo de AIMPLAS [Centro Tecnológico en el sector del plástico]. El objetivo era que los trabajadores pudieran realizar colectivamente una pieza escultórica. La figura sobre la que están puestas las botellas es una Cinta de Moebius.

Para terminar, una pequeña sorpresa, al menos para algunas de las personas que estéis leyendo esta entrada. El artista surrealista catalán Salvador Dalí, que siempre estuvo muy interesado por las matemáticas y la ciencia, también quedó cautivado por la cinta de Moebius.

Algunos de los grifos del Castillo Gala Dalí, o Castillo de Púbol, tienen diseños con la banda de Moebius. Por ejemplo, los grifos de la bañera de la sala de baño de Gala, que era la antigua cocina de este castillo gótico.

Así mismo, Salvador Dalí diseñó en 1970 una escultura con la forma de la Banda de Moebius, para ser realizada en pasta de vidrio por la casa Daum.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica