Que se rompan las cifras,
sin poder calcular
ni el tiempo ni los besos.
Y al otro lado ya
de cómputos, de sinos,
entregarnos a ciegas
–¡exceso, qué penúltimo!–
a un gran fondo azaroso
que irresistiblemente
está
cantándonos a gritos
fúlgido de futuro:
“Eso no es nada, aún.
Buscaos bien, hay más”.

Pedro Salinas, La voz a ti debida (1933). Poema [19], versos 726-739

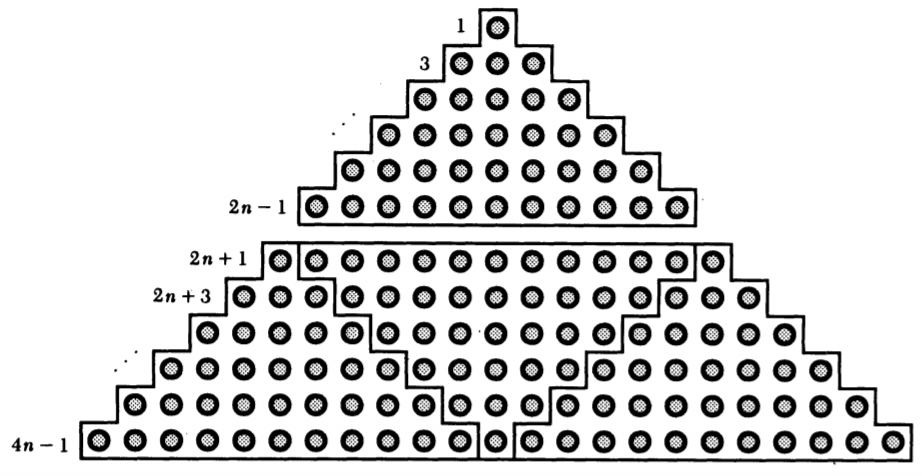
Este poema sobre cifras y cómputos habla de un amor sin límites. Me parece una hermosa manera de introducir una no menos bonita fórmula descubierta por Galileo en 1615:

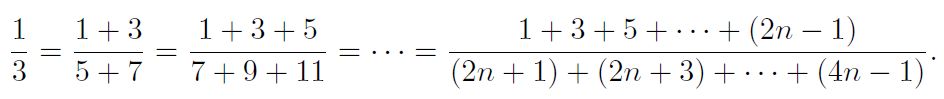
No es difícil probar esta fórmula por inducción matemática. Propongo una sencilla demostración en dos pasos.

Veamos en primer lugar que la suma de los n primeros números impares p(n) = 1 + 3 + 5 + … + (2n-1) es n².

Es claro que la fórmula es cierta para n=1 (1 = 1²). Suponiendo que se cumple para n (es decir, p(n) = n²), veamos que es cierta para n+1. En efecto,

p(n+1) =1 + 3 + 5 + … + (2n-1) + (2n+1) = [1 + 3 + 5 + … + (2n-1)] + (2n+1) = p(n) + (2n+1).

Aplicando la hipótesis de inducción, queda que:

p(n+1) = n² + (2n+1) = (n+1)².

En segundo lugar, comprobemos que la suma de los siguientes n números impares q(n) = (2n+1) + (2n+3) + … + (4n-1) es 3n².

La fórmula es cierta para n=1 (2 + 1 = 3 x 1²). Suponiendo que se cumple para n (es decir, q(n) =3n²), veamos que es cierta para n+1. En efecto,

q(n+1) =(2(n+1)+1) + (2(n+1)+3) + … + (4(n+1)-1) =

(2n+3) + (2n+5) + … + (4n+3).

Observar que esta suma tiene n+1 sumandos, obtenidos al eliminar de q(n) el primer elemento (2n+1) y al añadirle los dos sumandos (4n+1) y (4n+3). Es decir,

q(n+1) = q(n) – (2n+1) + (4n+1) + (4n+3).

Aplicando la hipótesis de inducción, queda que:

q(n+1) = 3n² – (2n+1) + (4n+1) + (4n+3) = 3n² + 6n + 3 = 3(n+1)².

La fórmula de Galileo es entonces cierta ya que:

p(n) / q(n) = n² / 3n² = 1/3.

El matemático Roger B. Nelsen es el autor del sugerente libro Proofs Without Words: Exercises in Visual Thinking (The Mathematical Association of America, 1997). En este texto propone una serie de pruebas sin palabras, es decir, demostraciones visuales, sin ninguna explicación, que ilustrarían una propiedad matemática que se desea verificar. La imagen que abre este escrito es precisamente una demostración visual de la fórmula descubierta por Galileo de la que hemos tratado en esta entrada: es la que propone Nelsen en la referencia [2].

Por cierto, la fórmula para la suma de los n primeros números impares también puede demostrarse sin palabras:

El primer cuadrado formado por un bloque negro muestra que p(1) = 1. Al añadir alrededor de él una tira de 3 bloques blancos (al sumar 1 + 3) se obtiene otro cuadrado y con ello se demuestra que p(2) = 4, y así sucesivamente…

Referencias

[1] Oddity, Futility Closet, 18 marzo 2021

[2] Roger B. Nelsen, Proof without words: On a property of the sequence of odd integers (Galileo, 1615), Mathematics Magazine, Vol. 68, no. 1, 1995, pág. 41.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad