En la anterior entrada del Cuaderno de Cultura Científica Los embaldosados de Truchet y el puzle del diamante estuvimos hablando del diseño de patrones de embaldosado realizados con una sencilla baldosa, la conocida con el nombre de “baldosa de Truchet”. Esta es una baldosa cuadrada dividida por la diagonal en dos zonas triangulares de dos colores distintos, por ejemplo, gris y negro, como la que aparece en la imagen.

En el siglo XVIII los religiosos franceses, interesados por las matemáticas, Sébastien Truchet –en su artículo Memoria sobre las combinaciones (1704)– y Dominique Doüat –en su libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722)– tomaron las cuatro orientaciones posibles de esta baldosa cuadrada bicolor, que vemos en la siguiente imagen, y realizaron un análisis combinatorio de los posibles patrones de teselados que se podían construir con ellas, del que hemos hablado en la anterior entrada.

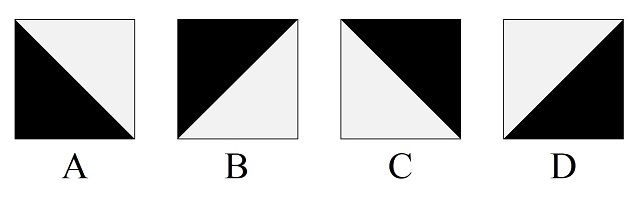
Y como comentábamos entonces, el estudio de los patrones de embaldosado o teselado, y en particular también los realizados con la baldosa de Truchet, es un tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. De hecho, tanto Truchet, como Doüat, no solo realizaron el estudio combinatorio de estos patrones de teselados, sino que se preocuparon de mostrar hermosos diseños realizados con esta baldosa, como los que aparecen en la siguiente imagen.

Es sorprendente como con un elemento tan sencillo se pueden realizar tan hermosos y complejos diseños de patrones de embaldosado. El propio Sébastien Truchet explicaba en su artículo Memoria sobre las combinaciones (1704) que para su estudio combinatorio se había inspirado en las baldosas de cerámica utilizadas para la decoración de un castillo que había visitado en uno de sus viajes, como hemos recogido en la entrada Los embaldosados de Truchet y el puzle del diamante. En la siguiente imagen se muestran, aunque no los azulejos que vio el religioso matemático en su viaje, sí unos azulejos decorativos antiguos. Pertenecen a la Catedral Santa María de la Huerta de Tarazona, edificio religioso que empezó a construirse a mediados del siglo XII, que como en la mayoría de edificaciones de este tipo tuvo sus etapas de destrucción y reconstrucción. Los azulejos pertenecen a las reconstrucciones de los siglos XV y XVI, de estilo mudéjar.

Así mismo, en la anterior entrada comentamos la presencia de estos cuadrados bicolor en el arte textil de los quilts. Pero también podemos ver como algunas artistas contemporáneas han utilizado, y siguen utilizando, estas ideas en sus obras de arte.

Las baldosas de Truchet en el arte contemporáneo

Por ejemplo, la artista noruega Josefine Lyche ha diseñado dos instalaciones con los patrones de teselado de las baldosas de Truchet que están relacionadas con el teorema del diamante en su versión 2 x 2 (véase Los embaldosados de Truchet y el puzle del diamante), que son The 2×2 Case (Diamond Theorem). After Steven H. Cullinane (2011) y The 2×2 Case (Diamond Theorem) II. After Steven H. Cullinane (2011). Estas obras consisten en la realización de los 24 diseños de embaldosados cuadrados de tamaño 2×2 que contienen las cuatro orientaciones distintas (A, B, C y D) de la baldosa cuadrada bicolor. La primera de ellas –que vemos en la siguiente imagen- realizada sobre una pared blanca con espejos que reflejan la luz dirigida hacia ellos en el lugar de exposición, una sala a oscuras, mientras que la segunda versión consiste en piezas realizadas en pintura acrílica sobre lienzo, en lugar de espejos.

La artista abstracta estadounidense Heather Jones, cuyo trabajo está inspirado en los diseños geométricos de los quilts tradicionales elaborados por las mujeres de ciertas regiones de Estados Unidos, ha creado algunas obras con esta estructura cuadrada dividida en dos triángulos coloreados. Por ejemplo, en la reciente exposición Storytellers / Contadoras de historias (2022) en el centro de arte contemporáneo de Dayton (Ohio), The Contemporary Dayton, dedicada a las mujeres desarrollaron el arte textil de los quilts, se ven algunas de estas obras, como las que vemos en la siguiente imagen: One way or another / De una manera u otra (2021), realizada en algodón cosido, destacando el color negro, y A time for change / Un tiempo para el cambio (2021), también en algodón cosido, destacando el color rojo.

O también, en la reciente exposición To Hold Tender This Land / Mantener joven esta tierra (2022) en la Galería David Richard de Nueva York se ha podido disfrutar de obras como la siguiente, titulada There was always light / Siempre hubo luz (2022).

Otra artista que utiliza este tipo de teselaciones es la francesa Ode Bertrand (1930) cuyo trabajo artístico está relacionado con la abstracción geométrica y el arte concreto, y que según sus palabras pretende “poner orden en el caos”. En una serie de obras, como la pintura Sin título (2015) que podemos ver en la siguiente imagen, añade a las cuatro teselas cuadradas bicolor blanco/negro, las dos teselas monocromáticas relacionadas, la tesela blanca y la negra.

Una artista que sigo a través de Instagram y cuyas obras, realizadas en lápiz sobre papel, son de una belleza geométrica inspiradora es la alemana Christiane Kaufmann (1983). Muchas de sus sencillas y hermosas creaciones nos recuerdan a la baldosa de Truchet, aunque muchos de sus cuadrados a lápiz son monocolor. En particular, la serie de obras titulada azul/rojo, de la que destaco esta pieza azul/rojo [25/10/2021],

que nos recuerda al diseño con baldosas de Truchet siguiente.

Una propuesta artística personal

Preparando esta entrada del Cuaderno de Cultura Científica se me ocurrió una idea para realizar una obra plástica basada en la baldosa de Truchet y el número pi, cuyo boceto explico en las siguientes líneas. Para empezar, renombramos las cuatro orientaciones de la baldosa cuadrada tricolor –antes nombradas A, B, C y D- como 1, 2, 3, 0, como se muestra en la imagen.

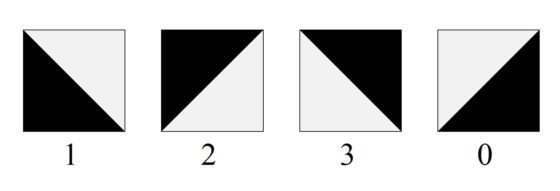
La idea es realizar un patrón de embaldosado cuadrado de tamaño 12 x 12 que formará la estructura visual de la obra. Para determinar la colocación de las cuatro baldosas de Truchet orientadas utilizaré el número pi, es decir, el diseño no depende de mis preferencias personales. Con este fin, consideramos la expresión decimal de esta constante matemática (sobre esta puede leerse la entrada ¿Es normal el número pi?), pero no en la base decimal que utilizamos normalmente, sino en base cuatro (en la que utilizamos las cuatro cifras básicas 1, 2, 3, 0), ya que solo tenemos cuatro orientaciones posibles. La expresión del número pi en base cuatro es la siguiente (en una futura entrada del Cuaderno de Cultura Científica explicaremos cómo determinar la expresión del número pi, o cualquier otro número, en una base de numeración cualquiera, por ejemplo, cuatro):

3,02100333122

220202011220

300203103010

301212022023

200031300130

310102210002

103200202022

121330301310

000200232332

221203230103

212302021101

102200201321…

Solo hemos incluido los 144 primeros dígitos del número pi, en base cuatro, ya que nuestro patrón es un cuadrado de tamaño 12 x 12 y utilizaremos 12 x 12 = 144 baldosas cuadradas. Estas estarán determinadas por el correspondiente dígito de pi, en base cuatro, recorriendo el cuadrado fila a fila, de arriba a la izquierda, hacia la derecha en cada fila, hasta abajo a la derecha. Así la primera fila de nuestro diseño de embaldosado utiliza las baldosas que se corresponden con los primeros doce dígitos 3 0 2 1 0 0 3 3 3 1 2 2, como puede observarse en el diseño final que hemos obtenido y que se muestra en la siguiente imagen.

En esta entrada solamente hemos considerado el caso de los diseños con la sencilla baldosa de Truchet, aunque podríamos considerar las baldosas de Truchet en un sentido más amplio, pero eso será en otra ocasión. Mientras os animo a realizar vuestros propios diseños con cuadrados bicolor, ya sea con telas, lápices de colores, pinturas o con el ordenador.

Bibliografía:

1.- Cyril Stanley Smith (con la traducción del texto de Truchet por Pauline Boucher), The Tiling Patterns of Sebastian Truchet and the Topology of Structural Hierarchy, Leonardo, vol. 20, n. 4, pp. 373-385, 1987.

2.- Dominique Doüat, Méthode pour faire une infinité de desseins différents avec des carreaux mi-partis de deux couleurs par une ligne diagonale : ou observations du Père Dominique Doüat, Religieux Carme de la Province de Toulouse, sur un mémoire inséré dans l’Histoire de l’Académie Royale des Sciences de Paris l’année 1704, présenté par le Révérend Père Sébastien Truchet religieux du même ordre, Académicien honoraire [Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal], París, 1922.

* Facsímil (extractos) e introducción de Jacques André

* Obra completa en Gallica – Bibliothèque nationale de France

3.- Sebastien Truchet, Memoir sur les Combinaisons, Histoire de l’Académie Royale des Sciences de Paris, 363-372 (1704).

* Obra completa en Gallica – Bibliothèque nationale de France

4.- Angel Requena, Simetrías I en la Catedral de Tarazona, del blog MateTurismo, 2018.

5.- Página web de Josefine Lyche

6.- Página web de Heather Jones

7.- Página web de Christiane Kaufmann

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica