José Manuel González Gamarro

La historia de la música de occidente se caracteriza por una gran riqueza de textos musicales, tanto de partituras como de libros analizando sus características y propiedades. Analizando los textos se puede saber cómo era la música de hace, por ejemplo, 500 años, no solo tocando la partitura, sino leyendo sobre cómo eran los instrumentos, la manera de componer o en qué contexto se escuchaba. Huelga decir que la música de hace cientos de años era muy diferente a la que se compone en la actualidad, ha ido transformándose, tanto en su forma como en su contenido. Una de las cosas que más ha variado a lo largo de la historia es la afinación. La palabra «afinación» tiene aquí una connotación muy amplia, pues no solo se refiere a cómo se templaban los instrumentos musicales, sino a cómo se concebían las consonancias y disonancias. Esto atañe también a la manera de cantar y a la percepción del oyente de cada época, es decir, hubo sistemas de afinación (incluso se daban con simultaneidad en el tiempo) que decidían lo que sonaba bien o mal, la delgada línea entre lo prohibido y lo permitido. Hay que tener en cuenta que la forma de concebir la afinación musical también ha variado a lo largo del tiempo, desde la mera comparativa hasta la estandarización de las vibraciones por segundo que le corresponde a cada nota.

La afinación pitagórica

Una de las afinaciones más usadas y de las que más literatura ha generado es la afinación pitagórica. Más allá de las leyendas e historias que se han ido difundiendo a lo largo de los años gracias a filósofos como Boecio, a la figura de Pitágoras se le atribuyen descubrimientos musicales en relación con las matemáticas que implican el inicio de la ciencia armónica.¹ Estos descubrimientos, a través supuestamente de experimentos con vasos de agua, pesos o flautas, se ejemplifican claramente en el monocordio. Este instrumento se compone de una sola cuerda y una regla numerada. Las consonancias se calculan según la parte de la cuerda que vibra. Teniendo en cuenta que la tensión de la cuerda es constante, si se divide justo a la mitad, el intervalo entre el sonido que produce la cuerda sin dividir y el sonido de la mitad de la cuerda es de una octava, es decir, la razón es 2/1. En otras palabras, si la nota de esa cuerda es, por ejemplo, un Do, al hacer vibrar solo la mitad de la cuerda volverá a sonar otro Do, pero una octava más aguda. Esto es solo un ejemplo puesto que el nombre de las notas como tal no se establecería hasta bastantes siglos después. Este intervalo de octava y esta proporción es la que se ha intentado mantener constante a lo largo de la historia y los diferentes sistemas de afinaciones. Pitágoras también definió los intervalos de quinta con la razón 3/2 (dividir la cuerda en tres partes iguales y hacer sonar dos) y el intervalo de cuarta con la razón 4/3. Según Arístides Quintiliano en su De Musica, el matemático recomendaba encarecidamente usar el monocordio para poder desechar la apreciación sensorial, es decir, decidir cuando existe consonancia mediante la apreciación intelectual, con puro cálculo numérico. Teniendo en cuenta que para sumar intervalos se multiplican sus razones y para restarlos se dividen, se pueden calcular los demás intervalos. Por ejemplo, el tono (una supuesta distancia aproximada entre Do y Re) es la diferencia entre la quinta y la cuarta y se calcula de la siguiente manera: 3/2 : 4/3 = 9/8. La diferencia entre la cuerda «al aire» y el sonido producido por la razón 9/8 es un tono.

Con el devenir de la historia, la música y los instrumentos musicales fueron ganando en complejidad. Además, para los pitagóricos las consonancias eran la cuarta, la quinta, la octava, la doble octava y la octava más la quinta. Todos los demás intervalos había que calcularlos en función de estos. Una consecuencia es la especulación matemática acorde con la musical, ya que, excepto la octava, ninguna consonancia puede dividirse en dos partes iguales, además tampoco se pueden sumar consonancias iguales para obtener otra consonancia. La suma de dos cuartas, por ejemplo, da como resultado una séptima, que no era una consonancia. El problema principal viene cuando queremos realizar una escala, es decir, una sucesión de tonos hasta llegar a la octava. Seis tonos (9/8) sucesivos sobrepasan la octava, no se llega exactamente al mismo sonido. Hay una pequeña diferencia llamada comma pitagórica. Esta diferencia oscila entre los 23 y los 23,45 cents según se pase a cents al final de hacer la comparativa entre octavas y quintas, o bien pasar a cents desde el principio y operar en cents directamente si escogemos esta unidad logarítmica para medir intervalos. No es algo desdeñable ya que un oído fino puede apreciar una diferencia de 3 cents. Este «pequeño» desajuste ha provocado diferentes sistemas de afinación que se han ido adaptando a la transformación de la música y los cambios en la concepción de los intervalos permitidos o consonantes. Ha habido sistemas de afinación circulares, que vuelven al mismo sonido (como el nuestro de la música occidental), repartiendo ese desajuste entre las notas de la escala, así como otros sistemas irregulares. De hecho, según Murray Barbour² ha habido más de 180 sistemas de afinación a lo largo de nuestra historia.

Toda esta complejidad tiene como consecuencia la creación de diferentes escalas y de diferentes instrumentos adaptados a estas escalas. Nuestra escala tiene siete notas (Do-Re-Mi-Fa-Sol-La-Si) que si las dividimos en semitonos iguales nos da la escala cromática de doce. Este es el límite de nuestra escala occidental. Sin embargo, a lo largo de la historia, debido a estos diferentes sistemas de afinación, han existido escalas de 31 o incluso de más de 50 sonidos diferentes. Para ello también se idearon instrumentos musicales acordes a las dificultades de la afinación, como el denominado Sambuca Lincea de los músicos Fabio Colonna o Scipione Stella con seis teclados en el mismo instrumento. Todo un desafío para los músicos de hoy en día.

El mesolabio de Eratóstenes

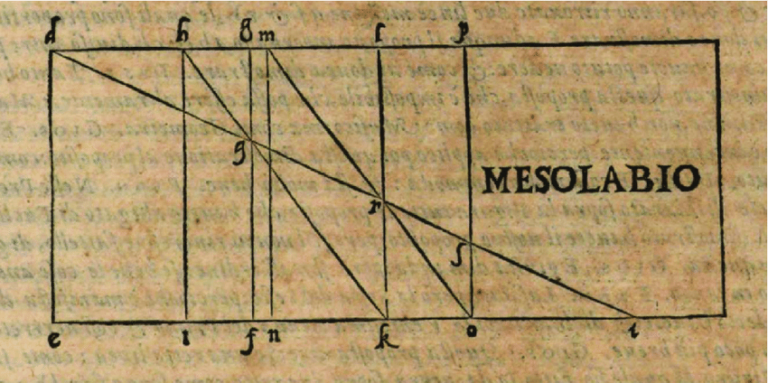
La supuesta insistencia de Pitágoras en evitar la apreciación sensorial deja insuficiente a la aritmética a medida que transcurre el tiempo debido a que, ya no solo hay que calcular quintas o cuartas, sino tonos y partes de comma. Esto último implicaría hallar medios, tercios, cuartos, etc. de esta distancia de 24 cents mediante sus razones por lo que habría que hallar la raíz cuadrada, cúbica, cuarta, etc. de la razón 81/80, dando cantidades irracionales. Esto propició la búsqueda de otras soluciones para algunos sistemas de afinación basadas en la geometría. Una de estas soluciones es utilizar un instrumento creado por Eratóstenes de Cirene (276-194 a. C.), el mesolabio. Esta especie de ábaco se compone de tres paralelogramos rectangulares que se mueven a lo largo de unas estrías, superponiéndose unos a otros. Se usa para hallar medias y proporciones y uno de sus primeros usos fue la duplicación del volumen de un cubo, como se explica en este vídeo, pudiéndose ver su funcionamiento a partir del minuto 10:00. Aunque el cálculo pueda parecer en un principio aproximado puesto que se trata de buscar los puntos de intersección, su uso evita las complicadas operaciones matemáticas que supone hallar distancias tan pequeñas. Moviendo rectángulos con diagonales trazadas y uniendo puntos con líneas rectas en las intersecciones, se calculan dos medias proporcionales en una razón superparticular, es decir, la razón de dos números enteros consecutivos. Esto encaja como anillo al dedo en las razones usadas en la música. Es un aparato que se usa muchos años después de su invención para el cometido de la afinación. Los músicos Gioseffo Zarlino y Pedro Salinas lo usarán y dejarán constancia de ello en sus tratados.

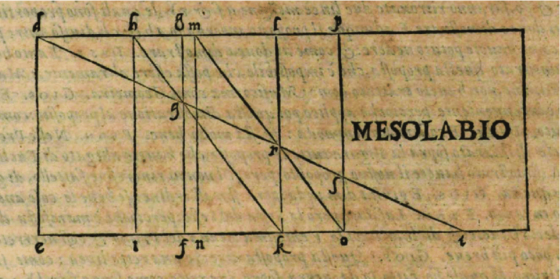
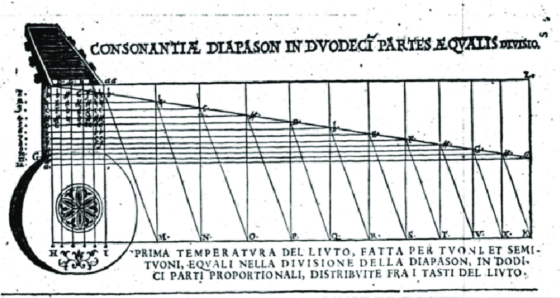
Aunque el cometido del mesolabio era encontrar dos medias, Zarlino indica que puede usarse para cualquier número de medias si se aumenta el número de paralelogramos. De hecho, este músico ilustra la división del mástil de un laúd mediante el mesolabio en el temperamento igual, doce partes iguales. También Pedro Salinas hace uso del añadido de paralelogramos para aumentar el número de medias, sin embargo, otros teóricos como el matemático Marin Mersenne sostienen que solo es posible su uso para dos medias.

Sea como fuere, Eratóstenes ideó un aparato que tuvo un uso muy prolongado en el tiempo y alejado de su primer cometido, otorgando una solución práctica a problemas que no existían en el tiempo en el que se concibió. Aunque su más conocida hazaña fue calcular la circunferencia de la Tierra, también fue capaz de inventar una especie de calculadora con un mecanismo muy sencillo y que fue muy significativo para el desarrollo de algunos sistemas de afinación de la música occidental. Este matemático que fue director de la Biblioteca de Alejandría tiene un papel primordial en la historia de esta disciplina, así como en la astronomía y la geografía, pero, aunque más discreto, también tiene un pequeño hueco en la historia de nuestra música.

Referencias: