José Manuel González Gamarro

Las sinergias son a veces clarividentes (e incluso imprescindibles) para los avances científicos de nuestra sociedad. La interdisciplinariedad es un objetivo a conseguir para poder avanzar cultural y socialmente. No podemos prescindir de la idea de que la realidad misma es interdisciplinar. Nuestra necesidad de parcelarla parte del hecho de poder entenderla. Estas sinergias nacen muchas veces de premisas alejadas, como ingredientes que, tras un análisis, alguien llegó a la conclusión de que mezclándolos podría elaborar una comida mucho más rica.

Tal es el caso de las matemáticas y la música. Seguramente ya habrá lectores que sepan que esta relación viene de lejos, de muy lejos, desde Pitágoras por lo menos. Y efectivamente es así. Sin embargo, la historia que aquí se cuenta tiene que ver con un matemático y físico francés que desarrolló una teoría para resolver una ecuación, en un principio bastante alejada del concepto musical: la ecuación del calor. Nuestro insigne matemático no podía ser otro que Jean-Baptiste Joseph Fourier (1768-1830), que además de ser el primero en dar una explicación científica del efecto invernadero, su teoría supuso un descubrimiento para poder explicar una cualidad del sonido como el timbre, que además tuvo consecuencias de toda índole para el desarrollo de la música. Lo que hizo Fourier, simplificando mucho, fue descomponer una forma de variación periódica, como puede ser una vibración de una onda sonora, en la suma infinita de otras formas sinusoidales (que siguen la función trigonométrica «seno»). Sin embargo, el primero en darse cuenta de que la cualidad del timbre dependía de la mezcla de estas vibraciones fue otro físico francés, Joseph Sauveur (1653-1716), quedando reflejado en su importante obra Traité de la Théorie de la Musique de 1697. Esta obra tuvo mucha importancia porque, años después, se originó un gran debate en torno a las cuerdas vibrantes que tuvo entretenidos a matemáticos como Daniel Bernoulli, Leonhard Euler, Jean le Rond D’Alambert o Joseph Louis Lagrange. Polémicas aparte, lo que hizo Fourier fue someter las ondas a tratamiento fisicomatemático.

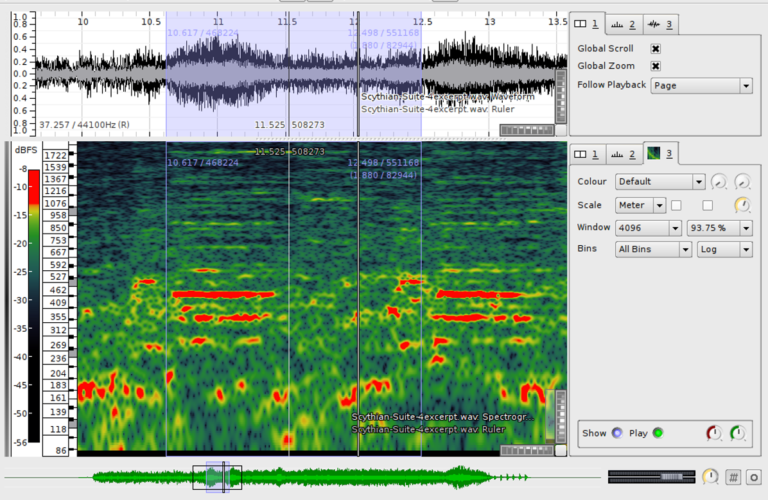
La altura de un sonido (si es más grave o más agudo) se mide en hercios (Hz), denominada frecuencia. Esta frecuencia indica el número de vibraciones por segundo. Por ejemplo, si cogemos un diapasón y lo golpeamos sonará la nota La de 440 Hz. Lo que nos dice el teorema de Fourier es que esa frecuencia en cualquier instrumento musical es el resultado de la suma de infinitas frecuencias que son múltiplos de la frecuencia fundamental (440 Hz). Si tocamos, por ejemplo, la segunda tecla correspondiente a la nota Do empezando por las notas graves en un piano, esa nota puede descomponerse en una serie de sonidos infinitos (sonidos armónicos). Al tocar la tecla lo que suena realmente es esto:

Para que todos estos sonidos se fundan en uno, sus frecuencias son múltiplos enteros de la frecuencia que se acaba sintetizando (lo que llega al oído). La suma de todos estos sonidos armónicos es el máximo común divisor y es el sonido que se percibe como único (el primero de la serie). Este fenómeno es de vital importancia para determinar el timbre. ¿Qué es lo que hace que un sonido suene a flauta, clarinete, piano, voz, etc.? Precisamente las diferentes amplitudes que le damos a cada uno de estos sonidos armónicos. Dicho de otro modo, si pudiéramos poner un control del volumen como el de una radio a cada uno de los sonidos armónicos, como se muestra en la imagen de más abajo, podríamos hacer que un mismo sonido sonara a violín o flauta tan solo girando algunos de estos botones.

Esto quiere decir que la intensidad de cada uno de los sonidos de la serie de los armónicos determinará el timbre. Estas intensidades relativas se pueden calcular con las fórmulas de Fourier. Gracias a esto, la informática ha revolucionado el mundo de la música, puesto que, si podemos calcular los timbres, podremos imitarlos, creando instrumentos virtuales prácticamente imposibles de distinguir de uno real en cuanto a esta cualidad sonora. Nunca se fíe el lector de las grandes bandas sonoras de las superproducciones, es altamente probable que detrás de lo que suena no haya ninguna gran orquesta sinfónica tocando detrás.

Gracias a la física y la matemática hemos podido entender cómo funciona el sonido y una de sus cualidades. Además, gracias a la sinergia física-matemática-música se creó una nueva disciplina: la acústica (término que usó por primera vez Sauveur). Pero este fenómeno sonoro (fenómeno físico-armónico) nos explica también otras cosas relacionadas con disciplinas humanísticas y menos científicas, como puede ser la historia de nuestra música occidental. Si nos fijamos en la serie de notas que aparecen en la figura de más arriba, podemos darnos cuenta de que no todas están a la misma distancia. Esta distancia o intervalo se mide contando las notas entre dos sonidos. Desde el primer sonido al segundo hay una octava porque desde un Do hasta el siguiente Do hay ocho notas (Do-Re-Mi-Fa-Sol-La-Si-Do). El tercer armónico es un Sol, por lo que del segundo al tercer armónico (Do-Sol) hay un intervalo de quinta (5 notas). A medida que avanzamos en la serie se ve claramente que las distancias se van reduciendo. Todas estas notas podrían prolongarse hasta el infinito, aunque no serían audibles a partir del umbral de escucha del ser humano, lo cual no significa que no estén ahí. ¿Y esta serie de notas explican nuestra historia? A medida que avanzamos en la serie, avanzamos en la historia. Veamos cómo.

Si nos remontamos a la antigua Grecia, su música se asemeja a la de la Alta Edad Media. En esencia era monofónica, es decir, solo había una melodía sin armonía, aunque hubiera diversos instrumentos que ornamentaran la melodía. El concepto de simultaneidad de dos sonidos no existía, entendidos como un intervalo. Lo que quiere decir que únicamente estaría el primer armónico o sonido fundamental, la primera nota de la serie. Si en un coro participaban hombres y niños, la diferencia fisiológica natural hace que los niños suenen una octava por encima de las voces de los hombres, aunque canten exactamente lo mismo. Ya tendríamos la octava, los dos primeros sonidos de la serie. Si seguimos el curso de la historia encontramos un tratado titulado Musica enchiriadis (ca. 900) donde se describen dos maneras de cantar de manera simultánea, llamado organum, duplicando la melodía a distancia de un intervalo de 5ª o 4ª, por lo que ya tendríamos hasta el armónico n.º 4 de la serie. Evidentemente existían otras distancias, pero se daban de manera fortuita, de pasada y no eran consideradas consonancias o intervalos idóneos donde hacer pausas musicales. Hasta el siglo XIII no aparece el intervalo de tercera en Inglaterra (avanzamos hasta el armónico 5 de la serie) como una consonancia, así como la sexta, o lo que es lo mismo, la distancia entre el armónico 3 y 5. El uso de notas alteradas de la música ficta en Francia (s. XIV) hizo que se distinguiera entre terceras mayores y menores, es decir, la distancia entre los armónicos 5 y 6 de la serie. El empleo de estos intervalos fue cada vez mayor, gracias a que la afinación pitagórica (división geométrica de una cuerda basada en quintas o en la proporción 3/2) fue cayendo en desuso hasta llegar a una afinación llamada mesotónica y el llamado temperamento igual (la afinación que se usa hoy en día en la música occidental) que favorecía la simultaneidad de estas distancias.¹

La concepción de la música como melodías diferentes que ocurrían simultáneamente (contrapunto) hizo que se oyeran otros intervalos de nuestra serie armónica, pero nunca concebidos como un punto estable donde finalizar o descansar momentáneamente. A principios del s. XVII esta visión empieza a cambiar hacia conceptos como el de acorde (en los armónicos 4-5-6) y tonalidad. En el s. XIX empieza a expandirse e introducir nuevas sonoridades y se van añadiendo notas a los acordes, aunque no en el orden exacto de la serie armónica.

Lo curioso de este fenómeno físico no es que nos resuma, grosso modo, la historia de la música occidental, sino que ha hecho que la historia de la música siga avanzando. Gracias al conocimiento de estos principios físicos e incluso su posibilidad de análisis mediante software específico, se han creado corrientes compositivas, como el espectralismo. Como su nombre indica, está basada en el espectro sonoro como materia prima para la composición de música. El análisis espectral permite conocer en una misma imagen la frecuencia principal con sus armónicos, la duración y la intensidad. Un ejemplo paradigmático de compositor espectralista es Gerard Grisey.

La física aporta nuevos caminos para la creación artística a la par que nos cuenta, con una mirada microscópica del sonido, el desarrollo de nuestra propia historia. La música, la física, la matemática… convergen no solo para tratar de contar la historia sino también para entenderla y buscar sus porqués gracias a la ciencia.

Referencia:

 
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.