Media, mediana y moda

Según los datos del estudio de estructura salarial que realiza el Instituto Nacional de Estadística (INE) en España, de media el salario en 2020 era de 25 165 € (en bruto, considerando los salarios a tiempo completo). Si eso implicara que la mayoría de los trabajadores a tiempo completo cobran esa cantidad, podríamos estar razonablemente satisfechos.
Lamentablemente, no es esa la realidad. El dato de 25 165 euros es la media. Pero si analizamos el salario mediano, es decir, aquel que se sitúa justo en la mitad del conjunto ordenado de salarios, fue de 20 920 €, sensiblemente más bajo.
Es más, el salario más frecuente (el salario modal o la moda de los salarios, otro valor estadístico) fue de 18 490 €. Es decir, lo más habitual es cobrar casi un tercio menos que el salario medio. ¡Hay casi 7 000 € de diferencia entre el salario más frecuente y el salario medio!
Media, mediana o moda, ¿cuál es mejor?
Cuando analizamos unos datos, ya sean de empleo, de salud o de consumo energético, deberíamos elegir el valor estadístico que mejor los represente. Pero para hacerlo es importante comprender conceptualmente el significado de cada una de las tres medidas de centralización que acabamos de utilizar: la media, la mediana y la moda.
- La media es el valor que resultaría de repartir equitativamente el total observado entre los individuos de la muestra.
- La mediana es el valor que divide la secuencia ordenada de observaciones en dos partes iguales.
- La moda es el valor más frecuente.
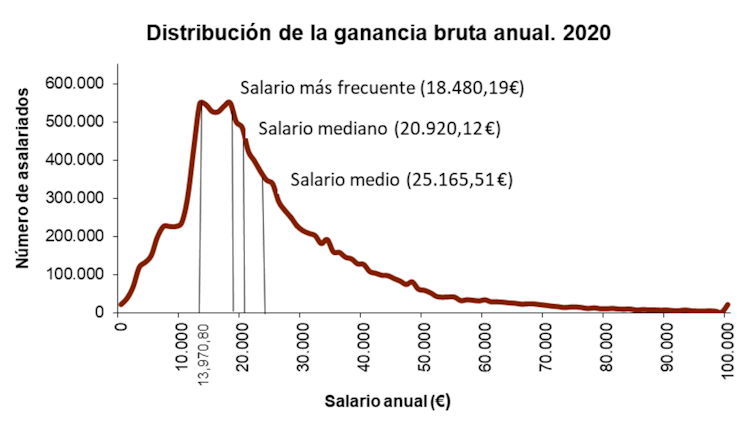
INE, Author provided
Además, conviene tener presente que para interpretar un conjunto de datos no solo cuenta su tendencia central: también hay que conocer su distribución. ¿Se parecen mucho los valores entre sí? ¿O hay valores muy distintos del valor central? Aquí es donde entran en juego otro tipo de medidas, las de dispersión, que nos informan de la lejanía o cercanía de los datos entre ellos y con respecto a alguna de las medidas centrales.
Cuando los valores extremos distorsionan los datos
Explicar por qué hay casi 7 000 € de diferencia entre el salario más frecuente y el salario medio es sencillo si hacemos un paralelismo con otra variable más sencilla de interpretar, como es el número de mascotas por familia.
Imaginemos que se estudia el número de mascotas en el hogar entre el personal de una oficina. La muestra nos ofrece 3 personas sin mascotas, 3 personas que tienen 1 mascota y otras 3 personas con 2 mascotas. En ese caso, dado que hay 9 observaciones, la mediana es la que ocupa la 5ª posición en la secuencia ordenada de valores:
0, 0, 0, 1, >1<, 1, 2, 2, 2
Es decir que la mediana es 1, porque nos deja 4 valores por debajo y otros tantos por encima, lo cual parece un valor bastante central. Coincide con la media, que resulta ser: (0+0+0+1+1+1+2+2+2)/9 = 1
Pero imaginemos que cambiamos a uno de los trabajadores con 2 mascotas por otro que tenga 20 mascotas. Es un numero elevado, sí, pero podemos pensar en que tiene, por ejemplo, peces. En ese caso, la media pasa a ser 3: (0+0+0+1+1+1+2+2+20)/9 = 3
La presencia de ese único valor anómalo (20 mascotas) ha triplicado la media. Ya no parece razonable pensar que el empleado típico tiene 3 mascotas, a la vista de la distribución. Sin embargo, ¿qué ha pasado con la mediana? Pues, con independencia de que el mayor valor haya pasado de ser 2 a ser 20, el valor 1 sigue ocupando la posición 5ª: 0, 0, 0, 1, 1, 1, 2, 2, 20
Por lo tanto, la mediana no ha cambiado por la presencia de ese valor anómalo.
Con ese ejemplo comprobamos la sensibilidad de la media a la presencia de valores anómalos o extremos (los llamados outliers en estadística), así como la mayor robustez de la mediana ante esa situación. Por este motivo, la media puede no ser una buena medida de tendencia central cuando en la muestra hay valores mucho mayores o mucho menores que el resto.
Cuando buscamos el valor central de distribuciones fuertemente asimétricas tiene más sentido tomar de referencia la mediana, como en los ejemplos anteriores del salario y el número de mascotas, y en general para variables socioeconómicas.
La mediana también suele ser una medida más fiel a la realidad central de unos datos cuando se estudia la supervivencia a una enfermedad o la respuesta a un medicamento, ya que puede haber individuos con respuestas muy anómalas (en estos casos, una supervivencia extraordinariamente longeva o una reacción muy adversa al medicamento).
Otras veces, la moda, a pesar de ser una medida que en muchas ocasiones no es muy informativa, tiene un valor fácilmente interpretable cuando entendemos el centro como la medida típica. El ejemplo inicial del salario nos podría servir: ¿cuál es el salario bruto más habitual en España? La respuesta sería la moda (18 490 €).
La media está sobrevalorada
Socialmente se le otorga excesivo valor a la media, algo que está relacionado con el denominado espejismo de proporcionalidad (ilusion of linearity, en inglés). Es decir, la tendencia a creer que lo proporcional es lo habitual, incluso lo justo.
Esta idea se refuerza desde la etapa escolar, cuando todas las calificaciones numéricas se obtienen calculando la nota media: socialmente se asume como la nota más “justa” o al menos la más indiscutible. Aunque no tiene por qué ser así. Pensemos en el carné de conducir: se repite el examen hasta que se supera, no se hace la media de los dos primeros intentos fallidos con el tercero exitoso. Ni desde luego se hace la media de las primeras clases en las que nos sentamos en el coche de la autoescuela con el día que aprobamos el carné.
Sin embargo, asumimos normal que tres controles realizados durante un trimestre hagan media con uno realizado al final. Y asumimos como indiscutible que si una estudiante obtiene en sucesivos exámenes 2, 9, 9 y 9, su nota media sea un 7,25. Si considerásemos la mediana como calificación más justa, obtendría un 9.
Exijamos gráficas para entender los datos
Lo que parece indiscutible es que, cuando únicamente proporcionamos la información de una medida central (ya sea moda, mediana o media), corremos el riesgo de que quien reciba la información construya una imagen mental que sitúe muchos, la mayoría o casi todos los valores de la variable en torno a ese valor central. Asimilando, por ejemplo, que “la mayoría de las personas en España tienen un salario bruto anual alrededor de 25 000 €”, cosa absolutamente falsa.
No solo es necesario saber dónde está el centro de los datos, también cuánto se separan los valores entre sí y respecto a la medida central (la dispersión) y de qué forma se disponen (más o menos simétrica, más o menos plana, etc.).
Por este motivo, resulta fundamental la visualización de los datos para hacerse una idea más aproximada a la realidad. En definitiva: desconfíen y pidan más información cuando les hablen solo de una media.![]()
Sobre el autor: Luis José Rodríguez Muniz, Catedrático del departamento de Estadística e Investigación Operativa y Didáctica de la Matemática, Universidad de Oviedo
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:

francesc
Excelente artículo, lástima que no puedo identificar a su autor/a
César Tomé
Lea hasta el final, ahí lo encuentra.