La expresión latina “vox populi”, cuya traducción literal sería “voz del pueblo” y que, según el diccionario de la lengua española de la RAE, es utilizada “para indicar que algo es conocido y repetido por todos”, fue el título de una carta que el polímata (antropólogo, geógrafo, explorador, inventor, meteorólogo, estadístico, psicólogo y eugenista) británico Francis Galton (1822-1911), que entre otras cuestiones fue un pionero en la identificación mediante huellas dactilares o en el estudio de la predicción del tiempo, publicó en la revista científica Nature en 1907.

El texto original de la carta Vox populi, publicada por Fancis Galton en la revista Nature, que podéis encontrar en la página de la propia revista o en la página web sobre Francis Galton, empieza así.

En estos días democráticos, cualquier investigación sobre la fiabilidad y peculiaridades de los juicios, u opiniones, populares es de interés. El material que vamos a discutir se refiere a un asunto menor, pero que viene al caso.

El asunto al que se refiere en su carta, y que utiliza para defender la “sabiduría de las multitudes” (del pueblo), tiene que ver con una visita que realizó a una feria anual de ganado voluminoso y aves de corral que había tenido lugar en la ciudad portuaria de Plymouth (condado de Devon, Inglaterra).

En su carta, Galton explica que en dicha feria de ganado se celebró una porra, es decir, una apuesta pública, para adivinar el peso de un buey ya descuartizado. Las personas participantes en la misma compraron, por un módico precio, una tarjeta en la que escribieron sus datos personales de contacto, así como su estimación del peso del buey descuartizado. Y los que más se acercaron a la cantidad real recibieron un premio. Entre las personas que visitaron la feria y se animaron a participar en la porra se enviaron 787 tarjetas, es decir, 787 estimaciones del peso del buey. Galton solicitó a las personas que organizaban la porra que le diesen dichas tarjetas para poder analizar estadísticamente los resultados de la misma, como así ocurrió.

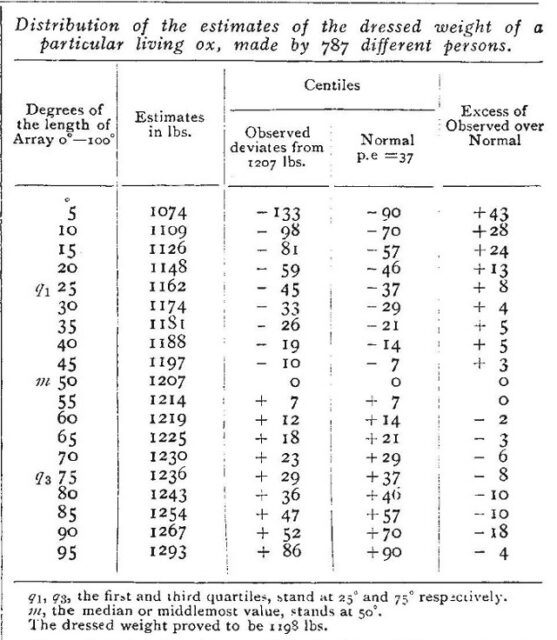
Con dicha información en su poder, ordenó todas las estimaciones sobre el peso del buey, que iban desde 1.074 libras (unos 487 kilos) hasta 1.293 libras (unos 586 kilos), y tomó el valor que estaba en el medio (lo que en estadística se llama la mediana), que era de 1.207 libras (unos 547 kilos), como el valor que podría ser más democrático, que podía representar el saber popular, ya que cualquier otra cifra (que no sea la que está en el medio tendrá a más de la mitad de las personas pensando que es muy alta o muy baja).

El peso que tenía el buey descuartizado objeto de la porra resultó que pesaba en realidad 1.198 libras (unos 543 kilos). Y podemos pensar, como así hizo Galton, que el valor del medio -el que recogía el saber popular- de 1.207 libras (547 kilos) estaba muy cerca del valor real, es decir, de las 1.198 libras (543 kilos) que hemos mencionado, solo se había desviado en 9 libras (4 kilos), que no es mucho. De hecho, la mediana, considerada por Galton como el valor más democrático, se alejaba menos de un 0,8% del valor real.

Ante lo que el científico comenta, en su carta, que este es un resultado “más digno de confianza para un juicio democrático de lo que cabría esperar”. Es decir, este es un buen ejemplo de cómo la estadística puede ayudar a obtener información de la realidad.

Por supuesto que esa “sabiduría de las multitudes” también es susceptible de ser manipulada. Imaginemos en el caso de la porra de la feria de ganado de Plymouth si alguien hubiese hecho correr el bulo de un peso alejado del real, como 1.150 libras, lo que habría provocado que muchas personas subestimaran el peso del buey descuartizado y la mediana se alejase más aún del peso real. Aunque para esta cuestión también podemos utilizar la estadística y extraer interesantes conclusiones, aunque ese es otro tema.

Bibliografía

1.- Francis Galton, Vox populi, Nature 75, pp. 450-451, 1907.

2.- David Spiegelhalter, El arte de la estadística, cómo aprender de los datos, Capitán Swing, 2023.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica