Os voy a confesar una cosa. Tengo un vicio, una pequeña (inofensiva) obsesión. Allá donde voy, saco fotos redondas. ¿Y qué son las fotos redondas, me preguntaréis? Pues bien, algo como esto… y tengo cientos.

Todo empezó como un juego hace bastantes años. Siempre que entraba en una iglesia, un palacete o una catedral, a mí me daba por fijarme en el techo. Me llamaba la atención lo siguiente: mientras que la mayoría de los cuadros y pinturas que nos rodean parecen basarse un sistema de representación cartesiano (arriba-abajo, izquierda-derecha), esos ejes se desdibujan en cuanto uno mira hacia arriba.

Es como si el mundo que nos rodea, y las pinturas que lo representan, estuviesen atravesados por finísimas líneas verticales que se extienden hacia el cielo. Esas líneas invisibles cuadriculan todo lo que crece sobre la Tierra, incluida nuestra mirada, que queda atrapada, obligada a girar sobre su eje. Pero se diría que, sobre nuestras cabezas, ese orden desaparece. Basta girar el cuello, colocarse de frente a la gravedad y las columnas invisibles del mundo desaparecen: arriba y abajo ya no ordenan el espacio, derecha e izquierda se desparraman en cualquier dirección.

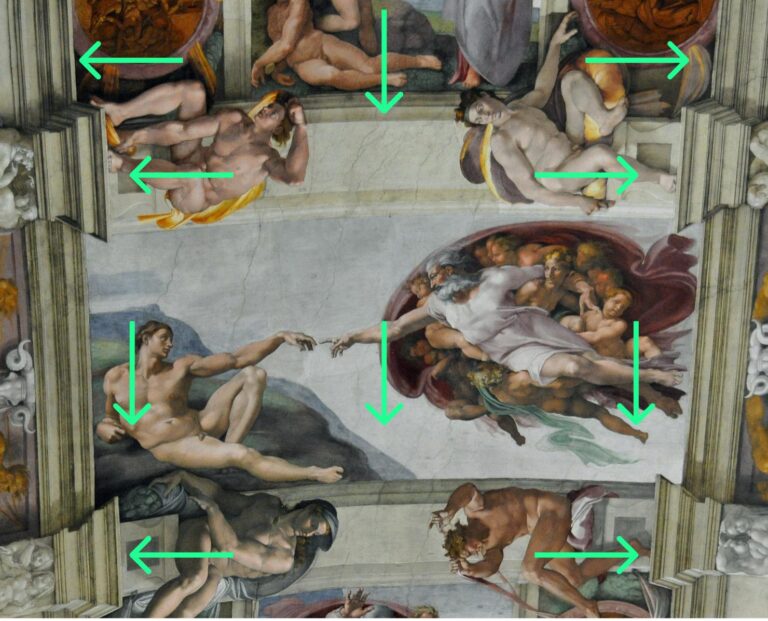
En este plano contrapicado, de hecho, lo más común es encontrarse con simetrías circulares. Por eso, la mayor parte de mis “fotos redondas” están sacadas con el objetivo apuntando hacia arriba. Capturan lámparas, cúpulas, bóvedas de todos los colores, formas y tamaños, pero sometidas casi siempre a algún tipo de simetría circular.

Fue esto lo que me dio una idea inicialmente: ¿y si representase estas imágenes en coordenadas polares, por así decirlo?, ¿sería posible hacer aún más evidente su simetría?

La idea fue creciendo hasta convertirse en un proyecto de fotografía (o una colección obsesiva, según se mire) y un programa de Python, elaborado junto a Iñaki Úcar. Pero para explicar bien en qué consiste, empecemos por la base: ¿qué es esto de las coordenadas polares y por qué debería importarte?

Un puente entre mundos matemáticos

Cuenta la leyenda¹ que Descartes inventó las coordenadas cartesianas mientras miraba una mosca. De niño había adquirido el hábito de quedarse en la cama hasta tarde, debido a las frecuentes enfermedades que lo aquejaban. Un día, vio al insecto moviéndose por el techo de su cuarto y se quedó embobado analizando su movimiento. Se preguntó cómo podría describirlo sin dibujar la trayectoria sobre un papel y se le ocurrió que, en cada momento, la posición de la mosca quedaba perfectamente definida por su distancia a dos paredes perpendiculares de la habitación. Esa reflexión le llevó a idear lo que hoy conocemos como geometría analítica, y comieron perdices. Fin.

La verdad es que no está muy claro siquiera que Descartes fuera el primero en describir las coordenadas²³ que hoy llevan su nombre. Pero el relato condensa de manera ejemplar la magia de los sistemas de coordenadas. ¡Es un invento que nos permite describir el espacio mediante números!, una idea tan poderosa que logró tender puentes entre dos mundos matemáticos separados durante siglos: el de la aritmética y la geometría.

Las coordenadas cartesianas definen un punto sobre un plano indicando su distancia a dos líneas perpendiculares. Las líneas son las paredes del cuarto de Descartes en el relato, o de manera más general, los ejes x e y (o eje de abscisas y eje de ordenadas). Pero esta no es la única manera de indicar una posición. Grégoire de Saint-Vincent y Bonaventura Cavalieri introdujeron el concepto de coordenadas polares de forma independiente a mediados del siglo XVII. En este sistema, cada punto de una superficie queda definido por su distancia al polo (el origen de coordenadas), y un ángulo que se define entre el eje de referencia, o eje polar y la línea que une el punto con el origen. Estas coordenadas a menudo se conocen como r (el radio) y θ (el ángulo). Podríamos usarlas para indicar la localización de cualquier punto de la Tierra respecto el polo Norte, por ejemplo⁴. Probablemente de ahí el nombre.

Estos dos sistemas de coordenadas son los que se utilizan más a menudo para describir una superficie plana (aunque no son los únicos, ni mucho menos). Ambos son equivalentes, igualmente poderosos a la hora de describir el espacio mediante números. Pero, a menudo, elegimos uno u otro en función de aquello que queremos describir. El propio sistemas de coordenadas, el lenguaje que usamos para describir el espacio, es capaz de absorber sus simetrías y simplificar así enormemente un problema.

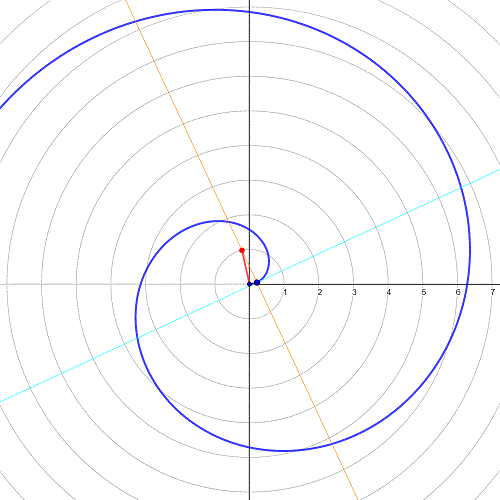
Quizás, el ejemplo más paradigmático es el de una espiral. Si queremos describir una espiral de Arquímedes en coordenadas polares, basta con una expresión tan simple como: . A medida que el ángulo de giro aumenta (θ), el punto se va alejando del origen (r). En cartesianas, la ecuación no solo es mucho más farragosa, también se vuelve mucho más difícil de interpretar: . En física es habitual enfrentarse a problemas, donde una condición de contorno, o un campo, se describe mucho más fácilmente en un sistema de coordenadas u otro. x_o

Pues bien, si aplicamos esta lógica matemática a cualquier tipo de sistema, decidme: ¿qué sistema utilizaríais para describir una fotografía como esta?

Fácil, ¿no? La imagen presenta, claramente, una simetría circular. En el próximo artículo os cuento cómo obtener y representar sus coordenadas polares, con un poquito de Python y mucho amor a la simetría.

Referencias y notas: