
Un amigo arquitecto me confesó una vez que su mayor limitación a la hora de construir viviendas es que la vida de las personas crece. Las casas, no. Por eso, los humanos tendemos a mudar la casa de cuando en cuando, para poder acoger nuevos muebles, cientos de libros, más y más recuerdos. Las caracolas no tienen esta opción. Ellas cargan de por vida con el mismo habitáculo que las vio nacer y solo con esfuerzo y saliva (baba de caracola, en este caso) consiguen ir ampliándola poco.
Lo curioso es que, en el proceso, su casa no cambia de forma. Da igual a qué distancia se mire, o bajo qué escala. La caracola siempre se parece a sí misma, con un poco más o menos de zoom. Este tipo de estructura es lo que se conoce como espiral logarítmica y obedece un patrón particularmente sencillo de crecimiento, a saber: “añade un poco más de baba, siempre en la misma dirección, mientras vas girando”. El resultado es sin duda elegante. Cada espira encaja en la anterior de acuerdo con una proporción fija. Cada fragmento de línea contiene el plan de su trazo entero, como un patinador que sólo necesitase fijar la posición de la cuchilla para dibujar la pirueta perfecta.

Jacob Bernoulli (1654-1705) llamó spira mirabilis (espiral maravillosa) a este tipo de curvas y les dedicó un tratado entero con el mismo título. Aunque las espirales logarítmicas ya habían sido descritas por Descartes, Bernoulli profundizó en su estudio y describió con gran detalle sus propiedades matemáticas. Quedó tan fascinado que pidió que grabasen una espiral maravillosa en la lápida de su tumba, acompañada por la frase latina “eadem mutato resurgo”: aunque transformado, resurjo igual. Antes de estas últimas palabras, el matemático suizo le había dedicado muchas otras a la espiral de la caracola y su característica autosemejanza. Para él, podía “ser usada como un símbolo, ya sea de fortaleza y constancia ante la adversidad, o como símbolo de la constancia del cuerpo humano, el cual después de todos sus cambios, aún después de la muerte, será restaurado a su exacta y perfecta esencia”. Jacob fue, sin duda, el mayor fan de la espiral logarítmica que ha existido jamás.
A pesar de esta especie de recursividad infinita, la longitud de una espiral logarítmica está perfectamente acotada. Gracias a la proporción fija que dicta la relación entre sus sucesivas espiras, estas forman una serie geométrica convergente. No existen las caracolas interminables. Incluso podemos calcular su longitud a partir de una simple foto de perfil, midiendo únicamente sus ángulos y su altura, como explico al final de este artículo.
Imagen: GIPHY
Por lo demás, la autosemejanza es, probablemente, la propiedad más llamativa de esta curva marina y matemática. Es la que la distingue, principalmente, de otra espiral igualmente común que hoy conocemos por el nombre de Arquímedes. El físico griego la describió extensamente en su libro Sobre las espirales del siglo III a. C. Es la figura que forman los muelles espirales, o los caminos pedregosos de los discos de vinilo. En esta espiral, las distancias entre los brazos permanecen constantes pero no se conservan las proporciones, ni la identidad a distintas escalas. Por un desdichado error, el artesano que preparó la lápida de Bernoulli grabó en ella una espiral de Arquímedes, en lugar de una logarítmica. El pobre matemático suizo, habría chillado de dolor de haber podido, después de muerto. Lo que me cuesta entender es que casi cuatro siglos después, nadie haya asaltado su sepultura para corregir semejante atropello.
¿Cómo calcular la longitud de una caracola?
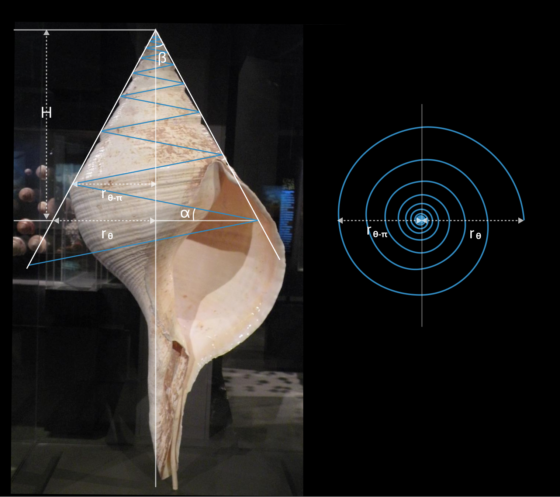
A vista de pájaro, la caracola describe una espiral plana que queda definida por la función r(θ) = ae bθ, en coordenadas polares. A partir de la fotografía y usando razones trigonométricas sencillas, como el teorema de los senos, es posible comparar la anchura de la caracola en su base y después de dar media vuelta. Esto nos permite estimar el valor de b,que caracteriza lo rápido que crecen la espiral logarítmica. Resulta que:
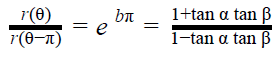
Conocido este parámetro, podemos integrar la función de la espiral para hallar su longitud en el plano, L = ae bθ/b, que no es más que el radio máximo de la espiral dividido por b. Si ahora desenroscamos imaginariamente la caracola, esta formará un canal en diagonal, de de base L y altura H. Por otra parte, el radio mayor de la espiral se relaciona con la altura mediante la relación tan α = ae bθ/H. Por lo tanto, la longitud total de la caracola vendrá dada por
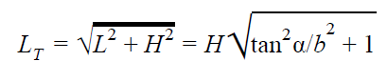
con  Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

La caracola más grave del mundo — Cuaderno de Cultura Científica
[…] 91 centímetros. Con este dato y gracias a las propiedades geométricas de su espiral logarítmica podemos calcular la longitud de su cavidad interna: unos 3 metros, según la foto que se encuentra en la Wikipedia. Ahora, para calcular su […]
Coordenadas polares — Cuaderno de Cultura Científica
[…] el ejemplo más paradigmático es el de una espiral. Si queremos describir una espiral de Arquímedes en coordenadas polares, basta con una expresión […]