Cuando presento alguno de mis libros en una librería, aunque la verdad es que esto no ocurre tantas veces como uno desearía, me gusta pedir a las personas que trabajan en la misma que me recomienden algunos libros, principalmente, novelas. En octubre (de 2023) presenté mi último libro “Las matemáticas como herramienta de creación artística” (Catarata / FESPM, 2023) en la librería Zubieta-TROA, de Donostia/San Sebastián. El responsable de esta librería, Adolfo López Chocarro, me recomendó varios libros, entre los cuales estaba el cuento El Ruletista (Impedimenta), del escritor rumano Mircea Cartarescu (Bucarest, 1956), en el cual se menciona, de pasada, la probabilidad de morir jugando a la ruleta rusa, en su versión en solitario. Y es de esto precisamente de lo que vamos a hablar en esta entrada del Cuaderno de Cultura Científica.

Mircea Cartarescu

El escritor y crítico literario Mircea Cartarescu está considerado el mejor escritor rumano de la actualidad y uno de los grandes escritores de la literatura europea contemporánea. La editorial Impedimenta ha traducido al español y publicado muchos de sus libros, como El Levante (Impedimenta, 2015), una epopeya heroico-cómica, que es también una aventura a través de la historia de la literatura rumana; el libro de relatos Nostalgia (Impedimenta, 2012), que se abría precisamente con el cuento El ruletista, y que consagró a Cartarescu como uno de los grandes escritores actuales de Rumanía; la novela Solenoide (Impedimenta, 2017), incluida en el listado de los mejores libros de ese año por la prensa cultural española e iberoamericana (que es parte de mi “tsundoku”, es decir, descansa en mi mesilla a la espera de ser leída); o Poesía esencial (Impedimental 2021), una recopilación de poemas escritos durante sus primeros años creativos. Para describir su filosofía como escritor, podemos acudir a una de sus citas, “Escribo porque quiero entender mi situación en el mundo”.

El Ruletista, un cuento de Cartarescu

Aprovechemos la contraportada de la publicación en español, por parte de la editorial Impedimenta, para introducir brevemente el cuento del que vamos a escribir en esta entrada del Cuaderno de Cultura Científica.

Prohibido durante años en Rumanía por lo explícito de su argumento, El Ruletista constituye uno de los más brillantes hitos narrativos de la reciente literatura europea. Esta pieza, tan breve como intensa, narra la improbable historia de un hombre al que nunca le ha sonreído la suerte, un desarraigado que sorprendentemente hace fortuna participando en letales sesiones de ruleta rusa. Multitudes enfervorecidas, presas del morbo, guardan cola para participar en las ceremonias de muerte y redención en que se convierten sus apariciones, y que dan paso a la histeria colectiva. Un escritor moribundo que conoció al Ruletista en su juventud intenta explicar cómo ese hombre insulso termina convirtiéndose en alguien inmortal y aparentemente inexpugnable, cuando en realidad en él solo anida el más desesperado espíritu de la autodestrucción.

Expliquemos en primer lugar en qué consiste el macabro juego de la ruleta rusa que es un elemento principal de este cuento. Mientras que en la ruleta rusa que hemos visto en duras películas como El cazador (1978), dirigida por Michael Cimino e interpretada por Robert de Niro, Christopher Walken, Meryl Streep, John Savage y John Cazale, se juega entre dos, o más jugadores, en el cuento El ruletista es una ruleta rusa solitaria, de un solo jugador.

Los principales protagonistas de la ruleta rusa de este relato son los siguientes. Por un lado, la persona que se juega la vida en la ruleta rusa, el ruletista, que en el cuento se explica que suele ser alguna persona que por diferentes circunstancias vitales no le importa jugarse la vida a cambio de dinero, normalmente, algún borracho, vagabundo o expresidiario, como se menciona más arriba “un desarraigado”. Luego está el patrón, que es quien contrata, o convence, al ruletista y que va a apostar a su favor, es decir, va a apostar a que esa persona que se juega la vida a la ruleta rusa va a sobrevivir a la misma. Y finalmente están los accionistas que son quienes apuestan en contra del patrón, esto es, ganan si muere el ruletista.

El juego consiste en lo siguiente. Primero se introduce una bala en el tambor de un revólver, que tiene capacidad para alojar seis balas (aunque hay revólveres que admiten otra cantidad de balas, cinco, seis, siete, ocho o diez balas), luego se gira el tambor y se cierra rápidamente para que la bala quede colocada en una posición al azar, entonces el ruletista coge el revólver, se apunta a la sien y dispara. Si tiene la suerte de que no salga la bala (lo cual ocurre en 5 de las 6 posiciones posibles del tambor, es decir, la probabilidad de que sea un disparo fallido es de 5 de cada 6 veces, el 83,33 %) el patrón gana, se queda con el dinero de los accionistas y le da al ruletista un diez por ciento de las ganancias. Por otra parte, si se dispara la bala (lo cual ocurre 1 de cada 6 veces, esto es, una probabilidad del 16,66 %), el ruletista muere y el patrón debe pagar a los accionistas entre diez y veinte veces la cantidad apostada por ellos, según hayan acordado. Es cierto, que el peso de la bala modifica algo estas probabilidades, pero no vamos a tenerlo en cuenta en esta entrada.

En el cuento hay dos protagonistas, el viejo escritor que escribe la historia del Ruletista y este, que se ha ganado el derecho a ser nombrado con la inicial mayúscula, ya que, como escribe el viejo escritor, “ha sido el único hombre al que fue concedido vislumbrar al infinito Dios matemático y luchar cuerpo a cuerpo con él”, refiriéndose a que este hombre ha jugado muchísimas veces a la ruleta rusa solitaria y siempre ha salido indemne, saltándose la “alta” probabilidad de morir. Como escribe el viejo escritor, referente a esto último:

“… el ruletista solo tenía cinco posibilidades entre seis de salvarse en la primera partida. Según el cálculo de probabilidades, si volvía a llevarse la pistola a la sien, sus posibilidades disminuían. En el sexto intento, esas posibilidades se reducían a cero. De hecho, hasta que mi amigo entró en el mundo de la ruleta, en el que llegaría a convertirse en el Ruletista con mayúscula, no se conocían casos de supervivencia ni siquiera tras cuatro intentos. La mayoría de los ruletistas lo eran, por supuesto, de forma ocasional, y no volverían a repetir esa terrible experiencia por nada del mundo…”

Y continuaba:

“… supongo que los accionistas apenas se fijaron en él cuando escapó con vida la primera o la segunda vez, puede que incluso la tercera. Fue considerado, como mucho, un ruletista afortunado. Pero después de la cuarta y de la quinta, se convirtió en la figura central del juego, un verdadero mito llamado a alcanzar proporciones gigantescas en los años posteriores. Durante dos años, hasta nuestro reencuentro en el restaurante, el Ruletista se había llevado el revólver a la sien en ocho ocasiones…”

Antes de entrar en el tema de las probabilidades, al que dedicaremos la siguiente sección de esta entrada, presentemos brevemente al Ruletista, a quien el viejo escritor conocía desde que eran niños. Desde siempre este perdía a todos los juegos, de pequeño a las canicas o el lanzamiento de herradura, cuando estuvo en la cárcel siempre perdía al póquer y cuando al salir de la misma se dedicó a la bebida e iba mendigando un trago de cerveza de mesa en mesa por las tabernas, los parroquianos de las mismas se lo jugaban con él al palillo más largo y, de nuevo, siempre perdía. El Ruletista era un candidato ideal para ser jugador de la ruleta rusa, pero, además, su malísima suerte en todo tipo de juegos hacía que en el caso de la ruleta rusa jugase a su favor, ya que podríamos decir que nunca “acertaba” con la bala en la posición de disparo y salía ileso del juego.

Un poco de probabilidad

Realmente hay diferentes cuestiones de probabilidad que se pueden analizar relacionadas con la ruleta rusa, pero vayamos exactamente a la situación descrita en este cuento. Empecemos por lo que ya sabemos y es evidente. Si un ruletista solo juega una vez a la ruleta rusa de un solo jugador, la probabilidad de sobrevivir es del 83,33 %, esto es, 5 de cada 6, mientras que la probabilidad de morir durante el juego es, la complementaria de la anterior, es decir, el 16,67 %, solo 1 de cada 6.

La siguiente cuestión que nos planteamos, siguiendo lo escrito en este pequeño relato, en extensión, no en calidad literaria, es la siguiente. Si el ruletista juega dos veces a la ruleta rusa, ¿cuál será la probabilidad de que muera o viva?

Pero cuidado, cada vez que se juega a la ruleta rusa la probabilidad es la misma que hemos comentado arriba, no cambia, ya que el juego, o el revólver, no tiene memoria. Lo que queremos conocer es la probabilidad de salir indemne, o respectivamente, morir, si se arriesga a jugar dos veces. Aunque no es necesario, podéis pensar en que ha decidido previamente jugarse la vida a la ruleta rusa solitaria en dos ocasiones. Calculemos esta probabilidad.

Recordemos brevemente, aunque realmente ya lo hemos utilizado, que la probabilidad de un evento es igual al número de casos favorables (del evento) dividido el número de casos posibles (del evento). Por ejemplo, si queremos conocer cual es la probabilidad de que salga un múltiplo de 3 si tiramos un dado, el número de casos favorables sería dos -que salga 3 o 6-, mientras que hay seis casos posibles -los seis valores del dado 1, 2, 3, 4, 5, 6-. Por lo tanto, la probabilidad de que salga un múltiplo de tres (3 o 6) al tirar el dado es 2 / 6 = 0,3333…, esto es, una probabilidad del 33,33 %.

Volvamos a la probabilidad de que el ruletista viva o muera si juega dos veces a la ruleta rusa. Primero veamos los casos posibles. Como en el primer disparo tenemos seis posibles posiciones del tambor del revólver o, dicho de otra forma, seis agujeros para disparar (que en la siguiente imagen hemos numerado como 1, 2, 3, 4, 5, 6) y en el segundo disparo tenemos otros seis posibles agujeros (de nuevo del 1 al 6 en la imagen), entonces el número de posiciones posibles de los tambores en los dos disparos o, mejor dicho, parejas de agujeros sobre los que disparamos son 6 x 6 = 36 (que podemos pensarlos como parejas de números, desde el (1, 1), (1, 2), (1, 3), hasta el (6,6)).

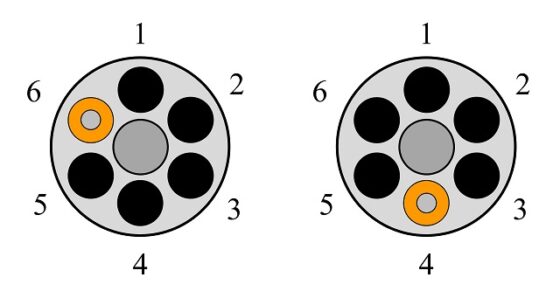
Ahora contemos cuántas parejas de agujeros serían favorables, si queremos calcular la probabilidad de que el ruletista salga indemne de las dos sesiones de la ruleta rusa. Como en el primer revolver hay 5 agujeros para los que el jugador vive, serán estos los que hay que tener en cuenta en la primera posición de la pareja de agujeros (en el ejemplo de la anterior imagen son los agujeros 1, 2, 3, 4, 5) y para cada uno de esos 5 agujeros, tenemos otros 5 agujeros en la segunda pistola que no contienen la bala de la muerte. Por lo tanto, el número de casos favorables, es decir, parejas de agujeros para los que el ruletista no muere, son 5 x 5 = 25. Por lo tanto, la probabilidad de que el ruletista quede con vida si juega dos veces a la ruleta rusa es 25/36 = 0,6944, es decir, una probabilidad del 69,44 %, mientras que la probabilidad de que muera es su complementario, 11/36 = 0,3056, esto es, el 30,56%.

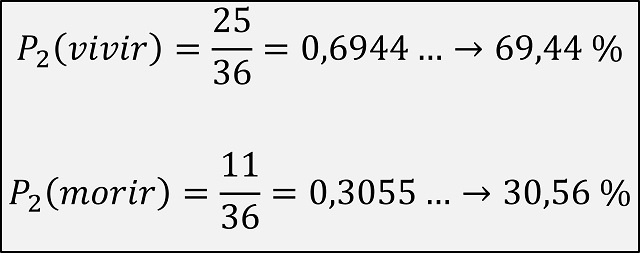
Aunque, si lo pensamos un poco, la probabilidad de salir indemne de las dos partidas de la ruleta rusa es la probabilidad de vivir en la primera partida (5/6) por la probabilidad de vivir en la segunda partida (5/6), es decir, (5/6)² = 25 / 36.

Esta forma de entenderlo nos permite obtener fácilmente la respuesta a la cuestión de qué probabilidades tiene el ruletista de vivir, o morir, si juega k veces a la ruleta rusa (para k = 1, 2, 3, 4, 5, …). De hecho, podemos obtener una fórmula en función del número k de partidas jugadas a la ruleta rusa por el ruletista.

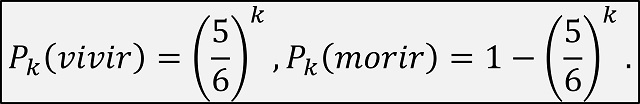
Ahora es fácil ir calculando la probabilidad de vivir o morir en función de cuantas veces juegue el ruletista a la ruleta rusa solitaria, que precisamente es de lo que habla, sin calcular probabilidades, el viejo profesor en los párrafos que hemos incluido más arriba. A continuación, incluimos una tabla con estas probabilidades para los casos en los que el ruletista juega entre una y diez veces, en la cual podemos apreciar la velocidad a la que la probabilidad de que el ruletista salga vivo va disminuyendo, y creciendo la probabilidad de morir.

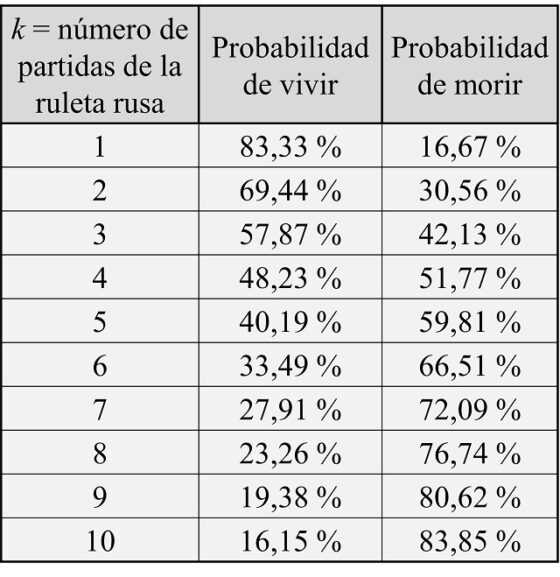
Podemos sacar entonces algunas conclusiones. Para empezar la probabilidad de morir es menor que el 50 % para los casos de una sola partida de la ruleta rusa (16,67 %), dos partidas (30,56 %) e incluso tres partidas (42,13 %). Luego en esos casos hay más probabilidades de ganar que de perder. El problema es que, si el jugador pierde, ha perdido algo tan importante e irrecuperable como es su propia vida. Además, cuando se dice que después de la tercera partida era considerado un ruletista afortunado, aun estando de acuerdo -ya que se está jugando la vida- podemos decir que no era tan excepcional, ya que la probabilidad de salir con vida seguía siendo, como hemos comentado, menor que el 50 %.

Justo se supera la probabilidad del 50 %, es decir, la misma que de sacar cara, o cruz, al tirar una moneda al aire, cuando se juegan cuatro partidas a la ruleta rusa. En concreto, hay una probabilidad del 51,77 % de morir y una probabilidad del 48,23 % de vivir. De hecho, cuando en el relato se escribe que “no se conocían casos de supervivencia ni siquiera tras cuatro intentos”, esto podríamos explicarlo como que los ruletistas no se atrevían a arriesgarse con la cuarta partida, porque lo que nos dicen los fríos números es que, a la larga, entre todos los jugadores que jugasen cuatro partidas, más o menos la mitad de los mismos vivirían y la otra mitad moriría.

Si continuamos, cuando se juegan seis partidas, la probabilidad de vivir no es cero, de hecho, es todavía relativamente alta, ya que es, más o menos, uno de cada tres casos. Aunque, como hemos dicho antes, el jugador no se juega dinero, sino su propia vida, por lo que la apuesta es demasiado arriesgada para él.

Por otra parte, el viejo escritor cuenta que cuando él se encontró con el Ruletista ya había superado 8 partidas de la ruleta rusa solitaria. Salir con vida de ocho partidas, como se ve en la anterior tabla es, más o menos, del 25 %, es decir, uno de cada cuatro casos. Luego, aun siendo algo excepcional, no es tan raro. Dicho de otra forma, si jugasen muchas personas a la ruleta rusa solitaria en ocho ocasiones, de media, una de cada cuatro viviría, aunque eso sí, tres de cada cuatro, moriría. A partir de ahí la probabilidad continúa cayendo cada vez más y más.

Por otra parte, en cierto momento del relato, el Ruletista empieza a incluir más balas en el revólver, aunque el cálculo de las probabilidades, para una cantidad de balas entre 1 y 6, es similar al realizado previamente, lo dejamos como diversión para las personas que están leyendo esto, si así lo desean.

Para terminar, me gustaría comentar que el objetivo de escribir esta entrada del Cuaderno de Cultura Científica no es corregir el cuento de Mircea Cartarescu, que es un cuento de una calidad excepcional, sino de aprovechar la mención a la probabilidad para hablar de la misma y calcular con exactitud cuál es esa probabilidad mencionada. De hecho, mi recomendación es que, si no lo habéis hecho ya, leáis este magnífico cuento.

Terminaremos con un poco de humor negro de la mano de El Mundo Today y la noticia en clave de humor cuyo titular es: Uno de cada ocho jugadores de la ruleta rusa no llega a fin de mes; así como con el cortometraje, también en clave de humor, Ruleta (2015), de Álvaro Carmona, que podéis ver aquí.

Bibliografía

1.- Mircea Cartarescu, El ruletista, Impedimenta, 2010.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica