La diferenciación automática es un campo bien conocido de las matemáticas aplicadas. Si quieres iniciarte en este mundo, no es necesario que implementes tu propio sistema desde cero. A menos que, como yo, quieras hacerlo. ¿Y por qué querría alguien en sano juicio hacer algo así? Mi motivación es sólo mía, aunque quizá a ti también te sirva. En el caso que nos ocupa ha sido una combinación de lo siguiente:

• Me gusta entender lo que hace el software que que utilizo.

• Resulta que la teoría detrás de la diferenciación automática es preciosa.

• Me estoy iniciando en el lenguaje de programación Julia, de modo que he usado este problema como ejercicio.

Además, si estás interesado en escribir código rápido y eficiente, es probable que prefieras centrarte en la diferenciación automática inversa (backward automatic differentiation), y no, como hice yo, en la diferenciación directa (forward automatic differentiation).

Si todavía estás leyendo, significa que después de todos estos avisos tu motivación intrínseca sigue intacta. ¡Genial! Permíteme presentarte el fascinante tema de la diferenciación automática y mi implementación. Es rápida y sucia, pero también pedagógica.

Que pasen los números duales

Probablemente las recuerdes de tus años en el instituto. ¡La pesadilla de las derivadas! Todas esas tablas que tenías que memorizar, todas esas reglas que tenías que aplicar… ¡puede hasta que sea un mal recuerdo!

¿Y si le enseñamos a un ordenador las reglas de la diferenciación? No solo es posible hacerlo, sino que incluso puede ser elegante. ¡Que pasen los números duales!

Un número dual es muy similar a un vector de dos dimensiones:

el primer elemento representa el valor de una función en un punto dado, y el segundo. su derivada en ese mismo punto. Por ejemplo, la constante 3 se escribirá como el número dual (3, 0) (el 0 significa que es una constante y, por lo tanto, su derivada es 0) y la variable x = 3 se escribirá como (3,1) (el 1 significa que 3 es una evaluación de la variable x, y por lo tanto, su derivada con respecto a x es 1). Sé que esto suena extraño, pero sigue leyendo unas pocas líneas más, todo se aclarará más adelante.

Tenemos en nuestras manos un nuevo juguete matemático. Si queremos divertirnos con él, tenemos que establecer las reglas del juego: comencemos definiendo la suma, la resta y la multiplicación por un escalar. Decidimos que estas seguirán exactamente las mismas reglas que los vectores:

Hasta ahora, poca emoción. La multiplicación se define de una manera mucho más interesante:

Fíjate bien en lo que pasa. ¿Por qué el segundo elemento tiene una regla de multiplicación tan rara? Pues porque dijimos que el segundo término representa una derivada, así que debe seguir la regla del producto para las derivadas.

¿Y qué pasa con los cocientes? ¡Exacto!… la división de números duales sigue la regla del cociente para las derivadas:

Por último, pero no menos importante, la potencia de un número dual a un número real se define como:

¿Sientes curiosidad por la multiplicación por u’? Corresponde a la regla de la cadena y permite que nuestros números duales nos sirvan para hacer algo tan deseable como componer operaciones.

Las operaciones definidas anteriormente cubren muchísimo terreno. De hecho, cualquier operación algebraica se puede construir utilizando estas operaciones como ladrillos básicos. Esto significa que podemos pasar un número dual a una función algebraica como argumento, y aquí viene la magia, el resultado será:

Ojo a lo que acabas de ver, porque es una pasada. ¡La ecuación anterior nos dice que simplemente alimentando a la función con el número dual (x, 1) devolverá su valor, ¡y además su derivada! ¡Dos por el precio de uno!

Los lectores familiarizados con los números complejos pueden encontrar interesante intentar el siguiente ejercicio:

Si definimos un número dual como

(u, u’) = u + e u’

con e² = 0, ¡todas las propiedades anteriores se satisfacen automáticamente!

Enseñando a hacer derivadas a tu ordenador

Ha llegado la hora de ensuciarse las manos: ¿cómo podemos implementar estas reglas de manera práctica en nuestro ordenador? Implementar un nuevo objeto (un número dual) con sus propias reglas de interacción es la tarea ideal para un lenguaje que permita programación orientada a objetos. La programación orientada a objetos es un paradigma de programación que permite definir no sólo las variables que un programa va a utilizar, si no también las reglas para interactuar con ellas. Curiosamente, el proceso es sorprendentemente similar al de enseñar a un estudiante humano. Con la diferencia de que nuestro «estudiante digital» nunca olvidará una regla, ni la aplicará de manera incorrecta ni se olvidará de un signo menos.

¿Qué aspecto tendrían estas reglas, por ejemplo, en Julia? (Para una implementación en Python, echa un vistazo aquí). En primer lugar, necesitamos definir un objeto Dual, que representa un número dual. En principio, es tan simple como un contenedor para dos números reales:

«»» Estructura que representa un número Dual «»»
struct Dual
x::Real
dx::Real
end

Este par de constructores nos vendrá bien más adelante:

«»» Estructura que representa un número Dual «»»
struct Dual
x::Real
dx::Real

«»» Constructor por defecto «»»
function Dual(x::Real, dx::Real=0)::Dual
new(x, dx)
end
«»» Si se pasa un Dual, simplemente devuélvelo
Esto será útil más adelante «»»
function Dual(x::Dual)::Dual
return x
end
end

No te preocupes demasiado si no entiendes las líneas anteriores. Se han agregado solo para que el objeto Dual sea más fácil de usar (por ejemplo, Dual(1) fallaría sin el primer constructor, al igual que la aplicación de Dual a un número que ya es un Dual).

Otro truco que resultará útil en breve es crear un alias para cualquier cosa que sea un Number (uno de los tipos base de Julia) o un Dual.

const DualNumber = Union{Dual, Number}

Y ahora viene la parte divertida. ¡Enseñemos a nuestro nuevo objeto cómo hacer matemáticas! Por ejemplo, como vimos antes, la regla para sumar números duales es sumar ambos componentes, al igual que en un vector 2D:

import Base: +

function +(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
return Dual(self.x + other.x, self.dx + other.dx)
end

Tenemos que enseñar a nuestro ordenador incluso cosas más básicas. Recuerda que una computadora carece por completo de sentido común, por lo que, por ejemplo, tenemos que definir el significado de un signo más delante de un Dual.

+(z::Dual) = z

Esto suena tan idiota como explicar que +3 es igual a 3, ¡pero el ordenador necesita saberlo!

Como quizá hayas imaginado, también será necesario definir la resta de un Dual:

import Base: –
-(z::Dual) = Dual(-z.x, -z.dx)

que a su vez nos permite definir la resta de dos números duales como una suma:

function -(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
return self + (-other) # Una resta disfrazada de suma!
end

Algunas operaciones básicas pueden ser un poco más complicadas de lo esperado. Por ejemplo, ¿cuándo es un número dual menor que otro número dual? Observa que en este caso, solo tiene sentido comparar los primeros elementos e ignorar las derivadas:

import Base: <
<(self::Dual, other::Dual) = self.x < other.x

Como vimos más arriba, cosas más interesantes ocurren con la multiplicación y la división:

import Base: *,/
function *(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x * other.x
dy = self.dx * other.x + self.x * other.dx # Regla del producto para derivadas
return Dual(y, dy)
end
function /(self::DualNumber, other::DualNumber)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x / other.x
dy = (self.dx * other.x – self.x * other.dx) / (other.x)^2 # Regla del cociente para derivadas
return Dual(y, dy)
end

y con la potenciación a un número real:

import Base: ^
function ^(self::Dual, other::Real)::Dual
self, other = Dual(self), Dual(other) # Forzamos la conversión en Dual
y = self.x^other.x dy = other.x * self.x^(other.x – 1) * self.dx # Derivada de u(x)^n
return Dual(y, dy)
end

La lista completa de definiciones para operaciones algebraicas se encuentra aquí. Para Python, utiliza este enlace. Te recomiendo echarle un vistazo.

Después de esto, cada vez que nuestro número dual encuentre una de las operaciones definidas anteriormente en su misterioso recorrido por una función o un script, llevará un registro de su efecto en la derivada. No importa cuán larga, complicada o mal programada esté la función, la segunda coordenada de nuestro número dual se encargará de llevar la cuenta. Siempre y cuando la función sea diferenciable y no lleguemos a la precisión de la máquina, claro… pero es que eso sería pedirle a nuestra computadora que haga magia.

Ejemplo

Como ejemplo, calculemos la derivada del polinomio:

en x = 3.

Para mayor claridad, podemos calcular la derivada a mano:

es evidente que y p(3) = 39 y p'(3) = 34.

Usando nuestro objeto Dual, podemos llegar a la misma conclusión automáticamente:

poly = x -> x^3 + x^2 + x
z = Dual(3, 1)
poly(z)
> Dual(39, 34)

El truco funciona incluso si el mismo polinomio está definido de una manera más fea y complicada:

«»» Equivalente a poly = x -> x^3 + x^2 + x, pero más feo «»»
function poly(x)
aux = 0 # Inicializamos una variable auxiliar
for n in 1:3 # Agregamos x^1, x^2 y x^3
aux = aux + x^n
end
end

poly(z)
> Dual(39, 34)

¿Y qué pasa si mi función no es algebraica?

El método esbozado anteriormente fracasará miserablemente en cuanto nuestra función contenga un elemento no algebraico, como un seno o una exponencial. Pero no te preocupes, basta con ir a nuestro libro de cálculo y enseñarle a nuestra computadora algunas derivadas básicas más. Por ejemplo, nuestra tabla de derivadas nos dice que la derivada de un seno es un coseno. En el lenguaje de los números duales, escribimos:

¿Y qué pinta u’ aquí? Una vez más, es la regla de la cadena.

La clave aquí es, y de hecho ha sido desde el principio:

Podemos crear una función, que llamaremos _factory, que genere una abstracción de esta estructura para mayor comodidad:

function _factory(f::Function, df::Function)::Function
return z -> Dual(f(z.x), df(z.x) * z.dx)
end

Con ayuda de esta función, solo tenemos que abrir nuestra tabla de derivadas y llenar línea por línea, comenzando con la derivada de un seno, continuando con la de un coseno, una tangente, etc.

import Base: sin, cos
sin(z::Dual) = _factory(sin, cos)(z)
cos(z::Dual) = _factory(cos, x -> -sin(x))(z) # A menudo se requiere una función lambda explícita

Si eres de los que prestaba atención en clase de matemáticas, ni siquiera necesitarás llenar todas las derivadas manualmente desde la tabla. Por ejemplo, la tangente se define como:

y ya tenemos el seno, el coseno y la división automáticamente diferenciables en nuestro arsenal. Entonces, basta con esta línea:

import Base: tan
tan(z::Dual) = sin(z) / cos(z) # ¡Podemos reutilizar las funciones definidas anteriormente!

Por supuesto, también es posible introducir la derivada de la tangente manualmente, y probablemente sea más eficiente y más estable. ¡Pero mola bastante que simplemente con la definición podamos apañarnos!

Aquí puedes ver una tabla de derivadas más extensa (o aquí, si prefieres Python).

Otro ejemplo

Probemos a derivar la siguiente función no algebraica:

Es fácil ver, con lápiz y papel, que la derivada es 1 en todas partes (fíjate que el argumento de la tangente es una constante). Pero veámoslo usando nuestro objeto Dual:

fun = x -> x + tan(cos(x)^2 + sin(x)^2)
z = Dual(0, 1)
fun(z)
> Dual(1.557407724654902, 1.0)

Para mayor conveniencia, podemos utilizar todo lo que hemos construido hasta ahora para crear un funcional (una función que devuelve funciones) que nos devuelva la derivada:

«»» derivative(f)

Devuelve la derivada de f
«»»
function derivative(f)
df = x -> f(Dual(x, 1.0)).dx
return df
end

Utilizando nuestro funcional, el ejemplo se vuelve aún más compacto y legible:

fun = x -> x + tan(cos(x)^2 + sin(x)^2)
dfun = derivative(f)
dfun(0)
> 1.0

Otro ejemplo

En este caso queremos calcular y además visualizar las derivadas de:

Primero, introducimos la función y usamos nuestro funcional para calcular su derivada.

f(x) = x^2 – 5x + 6 – 5x^3 – 5 * exp(-50 * x^2)
df = derivative(f)

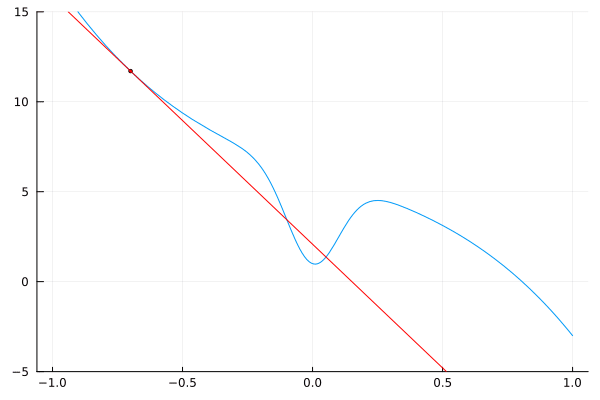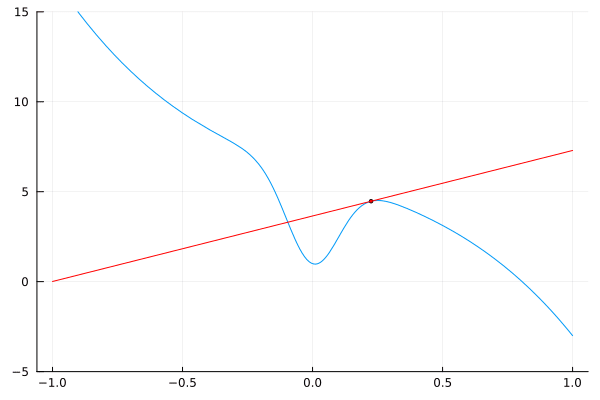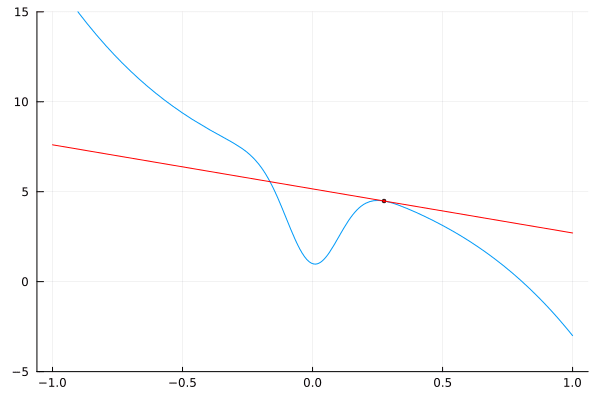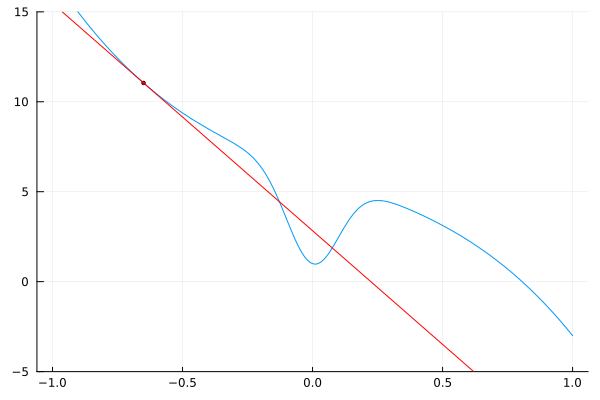
Podemos visualizar los resultados dibujando líneas tangentes a la función original.

using Plots
I = [-0.7; 0.7]
δ = 0.025
@gif
for a = [I[1]:δ:I[2]; I[2]-δ:-δ:I[1]+δ]
L(x) = f(a) + df(a) * (x – a)
plot(f, -1, 1, leg=false)
scatter!([a], [f(a)], m=(:red, 2))
plot!(L, -1, 1, c=:red)
ylims!(-5, 15)
end

¿Y esto para qué sirve?

La diferenciación automática es especialmente útil en el campo del aprendizaje automático (más conocido como machine learning), dónde es necesario calcular derivadas en varias dimensiones (también llamadas gradientes) con gran velocidad y exactitud. Dicho esto, la diferenciación automática en aplicaciones de aprendizaje automático suele implementarse de forma diferente a lo que hemos visto aquí. Por razones prácticas, suele utilizarse el «modo inverso» (backward), mientras que aquí hemos estudiado el «modo directo» (forward).

¿Por qué hemos estudiado el modo directo? Las razones han sido puramente pedagógicas: es más fácil de explicar y de entender.

Naturalmente, existen varias librerías capaces de hacer diferenciación automática. Un buen ejemplo es JAX (para Python). Otras librerías de aprendizaje automático, como Tensorflowo Pytorch también implementan esta función. En el caso de Julia existen también numerosas opciones, si bien Enzyme.jl parece llevar la delantera. Forwarddiff.jl también merece una visita, pues implementa precisamente lo que aquí hemos esbozado.

Doy las gracias a Abel Siqueira y a Aron Jansen por sus sugerencias y comentarios, que sin duda han hecho de este texto una mejor lectura.

Sobre el autor: Pablo Rodríguez-Sánchez es licenciado en ciencias físicas y doctor en matemáticas aplicadas. Actualmente es ingeniero de software de investigación en el Netherlands eScience Center.

Esta entrada es una traducción adaptada de Automatic Differentiation from scratch, publicada por el mismo autor en el blog del Netherlands eScience Center.