Uno de los problemas más frecuentes cuando los niños y las niñas de educación primaria empiezan a aprender las operaciones aritméticas y, más concretamente, los algoritmos para realizarlas, es entender y aplicar bien las denominadas “llevadas” que aparecen en dichos algoritmos. Veamos un ejemplo de suma y multiplicación con llevadas.

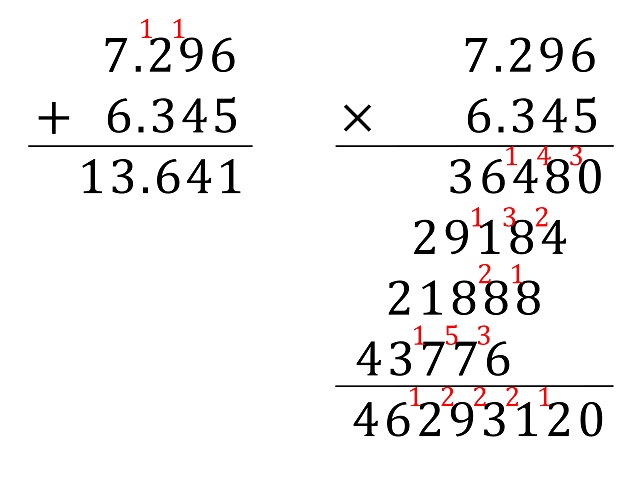
Definiendo una nueva aritmética

En 2003, al ingeniero estadounidense Marc Lebrun se le ocurrió definir una suma y una multiplicación especiales de números enteros no negativos, es decir, el cero y los números naturales, para las cuales no hacían falta las llevadas y bautizó a esta aritmética (suma y multiplicación) con el nombre de “dismal arithmetic” (que podría traducirse como aritmética deprimente o sombría) y que posteriormente sería rebautizada con el nombre, menos deprimente, de aritmética lunar, en contraposición a la aritmética natural, que podría considerarse que es la aritmética terrestre.

Para definir la suma y la multiplicación lunares, primero se definen las sumas y multiplicaciones entre las cifras básicas (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) y luego se extienden mediante los mismos algoritmos de suma y multiplicación normales pero cambiando las operaciones entre las cifras básicas por las nuevas operaciones, las lunares.

Vayamos con las cifras básicas. La suma lunar de dos cifras básicas es igual a la mayor de las dos cifras, así 3 + 7 = 7, 9 + 4 = 9 y 1 + 1 = 1, mientras que la multiplicación lunar de dos cifras básicas es la mínima de las dos, así 3 x 7 = 3, 9 x 4 = 4 y 1 x 1 = 1. Dicho de otra forma, sobre las cifras básicas la suma y multiplicación lunares son las operaciones máximo y mínimo de dos números, respectivamente.

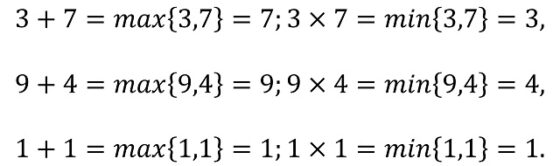
El siguiente paso, como se comentaba, es sumar y multiplicar (en la aritmética lunar) números con más de un dígito utilizando los algoritmos habituales de la suma y la multiplicación, pero utilizando las sumas y multiplicaciones lunares definidas para las cifras básicas. Veámoslo con dos ejemplos. En concreto, las mismas suma y multiplicación anteriores (7.296 + 6.345 y 7.296 x 6.345), pero con la aritmética lunar.

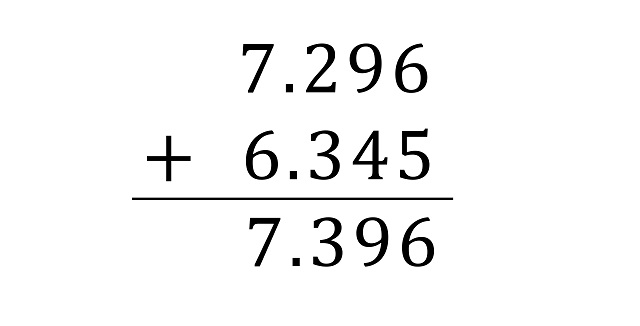
Como vemos, empezando por la derecha: 6 + 5 = 6, 9 + 4 = 9, 2 + 3 = 3 y 7 + 6 = 7, luego la suma nos da 7.396. Como no hay llevadas, y encima es simplemente considerar la operación máximo de los dígitos, es muy fácil de realizar.

Ahora, en la multiplicación vemos que la estructura es la misma, primero los productos parciales de los dígitos que componen los números (así, la primera fila es el resultado de multiplicar 5 por 7.296, la siguiente con 4, luego 3 y en la última fila se multiplica 6 por 7.296, para terminar sumando, con la suma lunar, esas 4 filas). El resultado es 6.366.455. Y de nuevo, es muy sencilla, ya que no hay llevadas.

Propiedades aritméticas de la suma y la multiplicación lunares

Lo siguiente que nos podríamos plantear, una vez definidas las operaciones aritméticas de la suma y la multiplicación lunares, es si satisfacen alguna de las propiedades de la suma y el producto normales. Recordemos cuales son dichas propiedades y veamos si se cumplen.

Dado un conjunto, llamémosle G (en nuestro caso, los números enteros no negativos), con una operación * (en nuestro caso la suma o la multiplicación lunares), de modo que a partir de dos elementos a y b del conjunto G, nos da un nuevo elemento, a * b, del conjunto G, las propiedades aritméticas habituales son las siguientes:

A. Propiedad conmutativa: a * b = b * a, para cualesquiera elementos a y b de G. Esta es una propiedad que cumplen la suma y multiplicación terrestres.

¿Qué ocurre con la suma lunar? Claramente es conmutativa para las cifras básicas, ya que a + b y b + a es simplemente tomar la mayor de las cifras entre a y b a + b = b + a = max {a, b}. Y para los números con más de un dígito también va a ser conmutativa, ya que la suma lunar es la suma lunar en cada una de las posiciones de los dígitos del número (unidades, decenas, centenas, unidades de millar, etc).

Si pensamos en la multiplicación lunar, para las cifras básicas también se cumple la propiedad conmutativa, ya que el producto es simplemente el mínimo de las cifras, esto es, a x b = b x a = min {a, b}. Y puede demostrarse que también se satisface para números de más de un dígito.

B. Propiedad asociativa: a * (b * c) = (a * b) * c, para todos los elementos a, b y c de G. De nuevo, es una propiedad que satisfacen las operaciones terrestres.

Respecto a las operaciones lunares, va a pasar algo similar a lo que ocurre con la propiedad conmutativa. Simplemente, comentemos que, para las cifras básicas, a + (b + c) = (a + b) + c = max {a, b, c}, y a x (b x c) = (a x b) x c = min {a, b, c}.

C. Elemento identidad, existe un elemento e de G tal que a * e = a = e * a. Para la suma normal el elemento identidad es el 0, mientras que para la multiplicación normal es el 1.

Para la suma lunar, el elemento identidad es el 0, ya que para cualquier número natural N, tenemos que N + 0 = N, puesto que en cualquier posición el dígito 0 nunca es el máximo, salvo que el otro sea el propio 0. Mientras que para la multiplicación lunar el elemento identidad es el 9, ya que N x 9 = N, en este caso porque 9 nunca es el mínimo de dos dígitos, salvo que el otro sea el propio 9.

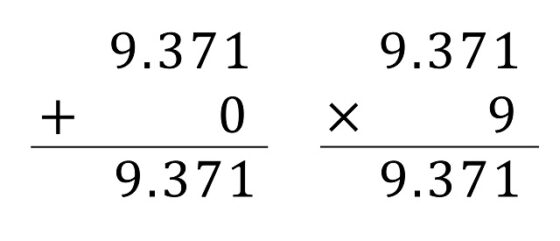
D. Elemento inverso, para cada elemento a de G, existe un elemento b (llamado inverso, y que suele denotarse como a^–1) tal que a * b = e = b * a. Para la suma terrestre el elemento inverso de un número a es el opuesto – a, luego existe el inverso si se consideran también los números negativos; mientras que el inverso de un número a es 1/a, luego tienen que considerarse los números racionales para que exista inverso.

Para la suma lunar no existe ningún número natural, es decir, no nulo, que tenga inverso. Y para la multiplicación lunar no existe ningún número, salvo 9, que tenga inverso.

Para terminar este apartado comentemos simplemente que la suma y multiplicación lunares nada tienen que ver con la idea intuitiva de la suma y multiplicación terrestres, ya que n + n no es dos veces n, esto es, es distinto de 2 x n, puesto que n + n = n y, en general, 2 x n no es n, por ejemplo, 2 x 3 = 2, 2 x 4 = 2 o 2 x 13 = 12. De la misma forma, n + n + n es distinto, en general, de 3 x n, y así para los demás casos.

Las tablas de la suma y multiplicación lunares

Para entender un poco mejor la suma y la multiplicación lunares podemos dar sus tablas de sumar/multiplicar asociadas. Empecemos con la suma. En la siguiente imagen se muestra la tabla de la suma lunar hasta el número 20 y he utilizado colores para entender mejor la operación. En concreto, cada uno de los diez colores determina la terminación de los números, es decir, la cifra de las unidades (por ejemplo, los números terminados en 3 son amarillos, 3, 13 y 23 en la imagen).

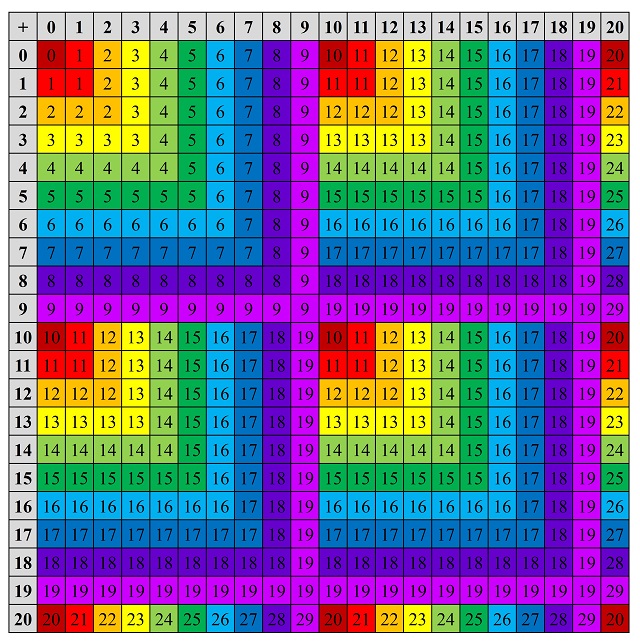
Por otra parte, en la siguiente imagen se muestra la tabla de la multiplicación lunar hasta el número 20 y, de nuevo, he utilizado colores para entender mejor la operación, de la misma manera que en la imagen anterior.

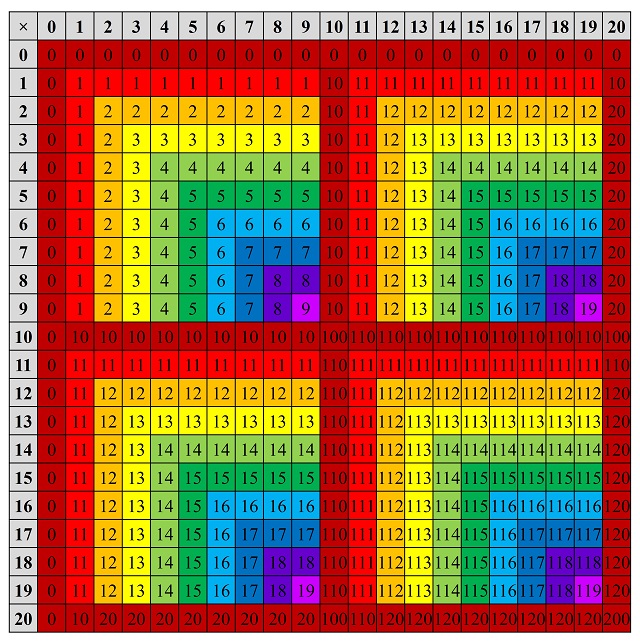
Algunas curiosas sucesiones de números

Para terminar esta entrada dedicada a la aritmética lunar, vamos a mostrar algunos ejemplos de sencillas sucesiones de números relacionadas con las operaciones lunares, como son la sucesión de los números pares lunares, es decir, los múltiplos lunares de 2; la sucesión de los números cuadrados lunares; la sucesión de los números triangulares lunares; o la sucesión de factoriales lunares, que aparecen mencionadas en el artículo Dismal Arithmetic, de David Applegate, Marc LeBrun y N. J. A. Sloane.

A. Los números pares lunares. Como ya se ha comentado más arriba, en la aritmética lunar no se cumple que 2 x n = n + n. Si vamos multiplicando los números enteros no negativos por 2 podemos observar que los primeros términos de esta sucesión (sucesión A171818 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) son los siguientes:

0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110. 111, 112, 120, 121, 122, 1.000, 1.001, 1.002, 1.010, 1.011, 1.012, 1.020, 1.021, 1.022, …

Aunque, a diferencia de los números pares terrestres, ahora los números pares pueden obtenerse como diferentes productos de 2 por otro número natural. Un par de ejemplos se muestran en la siguiente imagen.

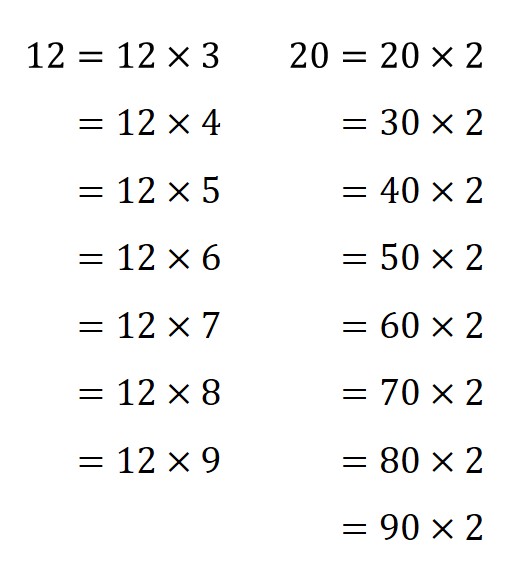
B. Los números cuadrados lunares. La siguiente sucesión está formada por los cuadrados de los números enteros no negativos, es decir, para cada n (= 0, 1, 2, 3, …), se toma n x n. Los primeros términos de esta sucesión (sucesión A087019 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) son

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 100, 111, 112, 113, 114, 115, 116, 117, 118, 119, 200, 211, 222, 223, 224, 225, 226, 227, 228, 229, 300, 311, 322, 333, 334, 335, 336, 337, 338, 339, 400, 411, 422, 433, 444, 445, 446, 447, 448, 449, 500, 511, 522, 533, 544, 555, 556, 557, 558, 559, 600, …

C. Los números triangulares lunares. Recordemos que los números triangulares (puede verse la entrada El asesinato de Pitágoras, historia y matemáticas (y II), o para más información el libro La gran familia de los números) son de la forma 1 + 2 + 3 + … + n, para n = 1, 2, 3, 4, etc. Los primeros términos de esta sucesión (sucesión A087052 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) son

1, 2, 3, 4, 5, 6, 7, 8, 9, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 49, 49, 49, 49, 49, 49, 49, 49, 49, 49, 59, 59, 59, 59, 59, 59, 59, 59, 59, 59, 69, 69, 69, 69, 69, 69, 69, 69, 69, 69, 79, 79, 79, 79, 79, 79, 79, 79, 79, 79, 89, 89, 89, 89, 89, 89, 89, 89, 89, 89, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, 199, …

Observemos, por ejemplo, que los números triangulares formados por la suma desde 1 hasta alguno de los siguientes números, 10, 11, 12, 13, 14, 15, 16, 17, 18 y 19, son todos iguales a 19, como se muestra en la siguiente imagen.

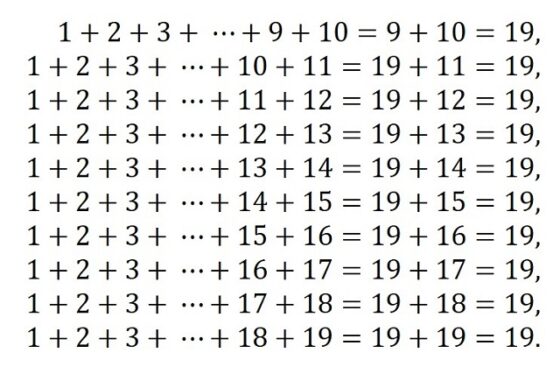
D. Los números factoriales lunares. En primer lugar, recordemos que los números factoriales (para el concepto de factorial de un número, véase la entrada Buscando lagunas de números no primos [https://culturacientifica.com/2018/06/27/buscando-lagunas-de-numeros-no-primos/]) son de la forma 1 x 2 x 3 x … x n, para n = 1, 2, 3, 4 etc. Por lo tanto, la sucesión de números factoriales lunares (sucesión A189788 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) empieza por los números

1, 1, 1, 1, 1, 1, 1, 1, 1, 10, 110, 1110, 11110, 111110, 1111110, 11111110, 111111110, 1111111110, 11111111110, 111111111100, 1111111111100, 11111111111100, 111111111111100, 1111111111111100, 11111111111111100, 111111111111111100, 1111111111111111100, 11111111111111111100, 111111111111111111100, 1111111111111111111000, …

Como podemos observar todos están formados por una serie de unos (1) consecutivos, seguidos de una serie de ceros (0) consecutivos. Podemos ver el cálculo de los primeros en la siguiente imagen.

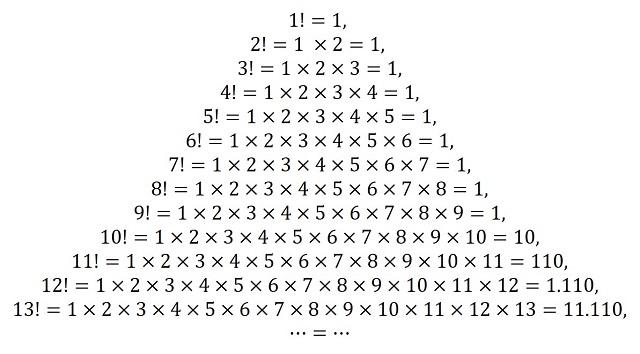
En esta entrada del Cuaderno de Cultura Científica hemos introducido la suma y la multiplicación lunares, hemos estudiado sus propiedades básicas y considerado algunas sucesiones de números relacionadas con esta aritmética lunar, pero se podrían seguir trabajando más cuestiones numéricas, por ejemplo, qué son los números primos lunares o si hay infinitos, pero de estas cuestiones ya hablaremos en alguna futura entrada.

Bibliografía

1.- David Applegate, Marc LeBrun, N. J. A. Sloane, Dismal Arithmetic, Journal of Integer Sequences 14, 2011.

2.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, de la colección Miradas Matemáticas, Catarata, ICMAT, FESPM, 2019.

3.- Raúl Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica