Acabo de terminar de leer la magnífica novela MANIAC del escritor chileno Benjamín Labatut. En cierto momento de la misma, se habla de cómo a finales del siglo XIX el matemático ruso-alemán George Cantor puso patas arriba el mundo de las matemáticas al echar por tierra las ideas sobre el infinito que se daban por buenas hasta ese momento, en particular, demostró que existía más de un infinito o que la cantidad de puntos de un segmento es la misma que la de un cuadrado. Aquí tenéis un fragmento sacado de esta novela.
Cantor fue un hombre extraordinario. Creó la teoría de conjuntos, una pieza clave de las matemáticas modernas, pero también contribuyó a la crisis fundamental cuando logró algo que parecía absolutamente imposible: expandió el infinito. Antes de Cantor, el infinito era considerado puramente como un constructo mental, sin ninguna correspondencia real en la naturaleza. Ilimitado e interminable, mayor que cualquier número, el infinito, si bien algo fantasioso, era una abstracción muy útil, y había demostrado ser una herramienta muy poderosísima. Armados con ella, podíamos estudiar cambios infinitesimales y considerar múltiples escenarios que eran simplemente impensables sin las maravillosas matemáticas del infinito, a pesar de que muchos sentían una desconfianza atávica hacia su mera existencia. Platón y Aristóteles detestaban la idea del infinito, y su rechazo se había vuelto la norma hasta que llegó Cantor a finales del siglo XIX y demostró que no había solo un tipo de infinito, sino una multiplicidad. Su tesis causó un caos que afectó a todas las ramas de las matemáticas, ya que su paisaje teórico –donde cada nuevo infinito parecía ser más vasto que todo lo que habíamos conocido antes- estaba lleno de nociones contradictorias y absurdos de carácter lógico que parecían haber surgido de la imaginación de alguna deidad enloquecida. Al utilizar sus nuevas ideas, Cantor podía demostrar que había tantos puntos en una línea de un centímetro como a lo largo de todo el espacio. Había dado un salto gigantesco hacia lo desconocido y encontrado algo único, algo que nadie siquiera consideró antes que él. Pero sus críticos, que eran muchos y variados, decidieron que había ido demasiado lejos. Por interesantes que fueran, sus infinitos jamás podían ser tomados como objeto serio de estudio. Sus ideas, dijeron, no eran más que un juego, un divertimento, un delirio más propio de la teología que de la matemática. Cantor se defendió con uñas y dientes, armado de una prueba que parecía irrefutable y que mostraba, con toda la belleza y la fuerza de la lógica, que él estaba en lo correcto: “¡La veo, pero no la creo!”, escribió a un amigo cercano cuando la terminó, y su mayor problema, a partir de entonces, fue que muchas otras personas fueron incapaces de aceptar ese nuevo artículo de fe.

En esta serie de entradas del Cuaderno de Cultura Científica, con el título de “El infinito en un segmento”, vamos a hablar sobre estas ideas revolucionarias de Cantor sobre el infinito.
Los números naturales
Para hablar del infinito vamos a considerar diferentes familias de números. La primera familia que fue inventada, o descubierta si somos más bien platónicos, por la humanidad, es la familia de los números naturales, que son los números que utilizamos para contar.
Números naturales = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, …}.
El primer paso que la humanidad realizó hacia el descubrimiento de los números naturales fue darse cuenta de que se podía comparar la cantidad de elementos de dos conjuntos estableciendo una correspondencia entre los elementos de ambos. Por ejemplo, si en una conferencia hay sillas libres, en las que no se ha sentado nadie, esto significa que hay más sillas que personas han acudido a la charla; por otra parte, si todos los asientos están ocupados y hay personas de pie, esto significa que hay más personas que sillas; y si todos los asientos están ocupados y no hay personas de pie, entonces hay las mismas sillas que personas. Si no se conoce el concepto de número, obviamente no es posible saber cuál es el número de personas que han acudido a la conferencia, pero sí se puede establecer si hay más personas o sillas, o son la misma cantidad. El acto de que una persona se siente en una silla es la correspondencia que se establece entre el conjunto de personas que acuden a la conferencia y el conjunto de sillas que hay en el recinto de la misma, que en el caso de que sean las mismas, se dice que se ha establecido una “correspondencia uno-a-uno” entre los elementos de los dos conjuntos.
Hace milenios los pastores podían comprobar, sin conocer los números, si todas las ovejas que habían sacado a pastar por la mañana regresaban a la tarde. Para ello, los pastores debían de colocar una piedra, u otro pequeño objeto, en algún recipiente, por cada oveja que salía a pastar al campo, y cuando regresaban, iban sacando una piedra por cada animal que llegaba. Sabían que habían regresado todas si al final no quedaba ningún guijarro en el recipiente, y que se había perdido alguna oveja, o habían sido atacadas por los lobos, si aún quedaban piedras.

El siguiente paso fue considerar familias de referencia respecto a las cuales comparar los conjuntos de objetos que se deseaba “contar”, que podían ser los dedos de las manos, piedras, nudos de una cuerda, muescas en el suelo, en un palo o en un hueso, para poder asociar cualquier cantidad de animales, plantas u objetos con el mismo número del conjunto de referencia. Así, dos ovejas se correspondían con dos dedos, dos muescas o dos piedras, cinco personas con cinco muescas. Este fue el origen del primer concepto, muy básico, pero un salto fundamental, de número desarrollado por la humanidad, así como el proceso de contar asociado, operación que consiste en añadir un objeto de referencia más por cada nuevo sujeto a contar. Esos elementos de referencia “inventados” se podían utilizar para “contar” cualquier conjunto de objetos y eran manejados por todas las personas de una misma zona.
Por lo tanto, en el nacimiento de los números naturales jugó un papel fundamental el concepto de “correspondencia uno-a-uno”, asociado al proceso de contar. Si queremos saber cuántas patas tiene un pulpo, contamos, es decir, establecemos una correspondencia uno-a-uno entre el conjunto de patas del pulpo y los números {1, 2, 3, 4, 5, 6, 7, 8}. Luego el pulpo tiene 8 patas.

Pero volvamos al conjunto de todos los números naturales. Si los intentamos contar, 1, 2, 3, 4, … 1.021, 1.022, 1.023, 1.024, … 2.345.678, 2.345.679, 2.345.680, 2.345.681, … no terminaríamos nunca. Cualquier número que consideremos (y hay números muy, muy grandes, como mostramos en la entrada Un paseo por los grandes números [https://culturacientifica.com/2022/11/16/un-pequeno-paseo-por-los-grandes-numeros/]), siempre podemos tomar números más grandes, de hecho, bastará con tomar el siguiente, sumarle 1, al mismo. Por lo tanto, el conjunto de los números naturales es un conjunto interminable, ilimitado, es decir, el proceso de contar sus elementos no tiene fin, por eso se dice que es un conjunto “infinito”.
Desde la antigüedad se conocía el concepto de infinito y que el conjunto de los números naturales es infinito, sin embargo, aunque durante siglos se trabajó con el infinito y sirvió para muchas investigaciones matemáticas, era un concepto un poco vago, asociado con lo interminable, lo ilimitado, una especie de número más grande que todos los números naturales.
Los números enteros
El conjunto de los números enteros está formado por los números naturales, el cero y los números negativos.
Números enteros = {… –9, –8, –7, –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …}.
Esta familia de números es también infinita, lo cual nos plantea una interesante cuestión. ¿Podemos comparar la cantidad de elementos de estos dos conjuntos? ¿Cuál de los dos conjuntos es más grande, tiene mayor cantidad de elementos? Por una parte, podemos pensar que el conjunto de los números enteros es mayor que el de los números naturales, puesto que este último está dentro del anterior. Pero, por otro lado, ambos conjuntos tienen una cantidad infinita de elementos, por lo que se pensaba que la cantidad de elementos era la misma, infinitos.
El matemático ruso-alemán George Cantor (1845-1918) utilizó la misma herramienta que se había utilizado en el origen de los números para establecer si dos conjuntos infinitos tenían la misma cantidad de elementos, la correspondencia uno-a-uno. Y efectivamente, los conjuntos de los números naturales y los números enteros tienen la misma cantidad de elementos puesto que se puede establecer una correspondencia uno-a-uno entre ambos. Podemos “contar” los números enteros, es decir, establecer esa correspondencia entre los números naturales {1, 2, 3, 4, 5, 6, 7, …} y los enteros, de la siguiente forma: 0, 1, –1, 2, –2, 3, –3, 4, –4, 5, –5, … Es decir, estamos estableciendo la correspondencia uno-a-uno mediante la posición, el orden en el que contamos. En consecuencia, la cantidad de elementos del conjunto de los números enteros es igual al de los números naturales.

En matemáticas, un conjunto (infinito) se dice que es numerable si se puede establecer una correspondencia uno-a-uno con el conjunto de los números naturales.
Por lo tanto, el conjunto de los números enteros es numerable.
Que el conjunto de los números enteros, que contiene al conjunto de los números naturales, sea numerable nos lleva a una primera propiedad paradójica del infinito (la conocida paradoja de Galileo), que no se cumple la propiedad de los conjuntos finitos de que “el todo es mayor que la parte”. Otro ejemplo de esta propiedad paradójica del infinito es que hay la misma cantidad de números naturales, que la cantidad de números pares, aunque los números pares son solo una parte de los números naturales. La correspondencia uno-a-uno canónica entre ambos conjuntos es la siguiente, a cada número natural n le corresponde el número par 2n.
Precisamente, el hotel infinito de Hilbert, que presentó el matemático alemán David Hilbert (1862-1943) en una conferencia de 1925, es un conocido experimento mental que pone de manifiesto esta propiedad paradójica del infinito. El experimento mental nos dice que “un hotel completo con infinitas habitaciones puede acomodar a nuevos clientes que lleguen, incluso si estos son infinitos, e incluso este proceso se puede repetir una cantidad infinita de veces” (podéis ver el video que grabamos para la sección Una de mates, del programa de televisión Órbita Laika: El hotel infinito).


Los números racionales
La siguiente familia de números es la familia de los números racionales, que incluirá a los números enteros, luego también a los números naturales. Los números racionales, o fraccionarios, son aquellos números que se expresan como cociente a / b de dos números enteros a y b. Por ejemplo, los cocientes 1 / 2, 7 / 9, 1 = 1 / 1, –5 / 3 o –4 / 37, por mencionar algunos.
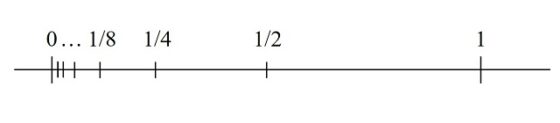
Los números racionales son infinitos, pero además tienen una propiedad muy interesante, la conocida propiedad arquimediana, que nos dice que entre cualesquiera dos números racionales siempre existe otro número racional intermedio. Por ejemplo, entre 0 y 1 está 1 / 2, entre 0 y 1 / 2 está 1 / 4, entre 0 y 1 / 4 está 1 / 8, y así indefinidamente.
Esta propiedad nos lleva al relato El libro de arena del escritor argentino Jorge Luis Borges (1899-1986), a quien le apasionaba el tema del infinito. En él se desafía a Borges a abrir el libro por la primera página:
Me dijo que su libro se llamaba el Libro de Arena, porque ni el libro ni la arena tienen ni principio ni fin.
Me pidió que buscara la primera hora.
Apoyé la mano izquierda sobre la portada y abrí con el dedo pulgar casi pegado al índice. Todo fue inútil: siempre se interponían varias hojas entre la portada y la mano. Era como si brotaran del libro.
-Ahora busque el final.
También fracasé; apenas logré balbucear con una voz que no era la mía:
-Esto no puede ser.
La portada del libro de arena sería el 0, la contraportada el 1, y las hojas se corresponderían con los números racionales entre 0 y 1. Por cierto, que el título de este relato parece dar nombre a la novela gráfica de Paco Roca que hemos mencionado arriba, Las calles de arena.
La propiedad arquimediana nos sugiere que hay una gran cantidad de números racionales, que están muy apretados, muy juntos unos de otros, no solamente existe una infinidad de número racionales, sino que entre cualesquiera dos números racionales también existen infinitos números racionales. Esto nos lleva a pensar que quizás el infinito de los números racionales es mayor que el infinito de los números naturales, o dicho de otra forma, que los números racionales no se pueden contar. Sin embargo, para nuestra sorpresa, esto no es así, hay tantos números racionales como números naturales.
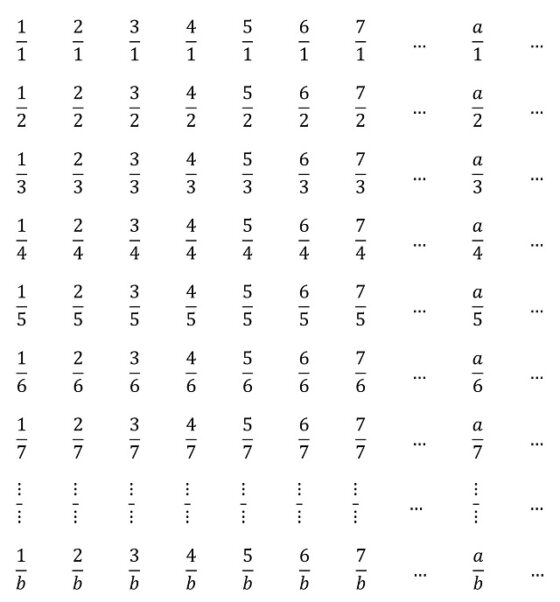
Demostremos primero que los números racionales positivos son numerables, haciendo uso del método diagonal que utilizó el propio Cantor. Para ello tengamos en cuenta que los números racionales positivos son de la forma a / b, con a y b números naturales. Por lo tanto, vamos a representarlos en una retícula “infinita” en la cual los números de la primera fila tendrán el 1 en el denominador, mientras que el numerador serán los números naturales empezando desde 1 en cada columna, los de la segunda fila tendtrán el 2 en el denominador y el numerador como en la primera fila, y así para las demás filas, como en la siguiente imagen. Por lo tanto, un número de la forma a / b estará en la fila b y en la columna a.
Una vez distribuidos de esta forma, los vamos a contar de forma diagonal, como aparece en la siguiente imagen.
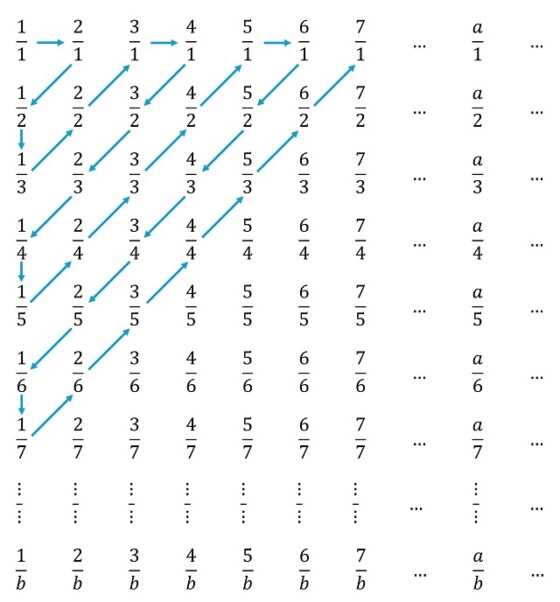
Por lo tanto, estaríamos “contando” (estableciendo una correspondencia uno-a-uno con los números naurales) los números de la forma a / b de la siguiente forma
1, 2, 1/2, 1/3, 2/2, 3, 4, 3/2, 2/3, 1/4, 1/5, 2/4, 3/3, 4/2, 5, 6, 5/2, 4/3, 3/4, 2/5, 1/6, 1/7, 2/6, 3/5, 4/4, 5/3, 6/2, 7, …
Aunque de esta forma hay números que estamos contando más de una vez, por ejemplo, todas las fracciones de la forma n / n son iguales a 1, todas las fracciones de la forma n / 2n son iguales a 1 / 2, o las de la forma 3n / 4n son iguales a 3 / 4. En general, si a y b tienen factores comunes, la expresión a / b puede simplificarse a una extresión a’ / b’ de forma que a’ y b’ no tienen factores comunes. En concreto, si n es el factor común de a y b, es decir, a = a’ x n y b = b’ x n, entonces

Por lo tanto, solo consideramos las fracciones de la forma a / b, donde a y b no tienen factores comunes y al contar las fracciones según el orden diagonal anterior, saltamos las fracciones con factores comunes, quedando así (al empezar a contar):
1, 2, 1/2, 1/3, 3, 4, 3/2, 2/3, 1/4, 1/5, 5, 6, 5/2, 4/3, 3/4, 2/5, 1/6, 1/7, 3/5, 5/3, 7, …
En conclusión, los números racionales positivos son numerables. Y ahora, utilizando el mismo argumento que para los números enteros, puede demostrarse fácilmente que todos los números racionales son numerables, contando primero el 0 y después utilizar el orden anterior pero incluyendo los negativos, con ese mismo orden, de forma alternada.
0, 1, –1, 2, –2, 1/2, –1/2, 1/3, –1/3, 3, –3, 4, –4, 3/2, –3/2, 2/3, –2/3, 1/4, –1/4, 1/5, –1/5, 5, –5, 6, –6, 5/2, –5/2, 4/3, –4/3, 3/4, –3/4, 2/5, –2/5, 1/6, –1/6, 1/7, –1/7, 3/5, –3/5, 5/3, –5/3, 7, – 7, …

Una cuestión interesante a destacar en la demostración de la numerabilidad de los números racionales (positivos) es que ya no es posible “contar” con un orden “natural” en el que se mantenga el orden del valor de los números, es decir, que se cuentan los números de menor a mayor.
Por otra parte, la forma de ordenar los números racionales, es decir, de establecer la correspondencia uno-a-uno con los números naturales no es única. Por ejemplo, otro orden posible, para los números racionales positivos, sería ordenar las fracciones a / b, con a y b sin factores comunes, según el valor de la suma a + b, desde 1 en adelante, y con a de menor a mayor (o lo que es lo mismo, b de mayor a menor), como se muestra a coninuación.
1/1, 1/2, 2/1, 1/3, 3/1, 1/4, 2/3, 3/2, 4/1, 1/5, 5/1, 1/6, 2/5, 3/4, 4/3, 5/2, 6/1, 1/7, 3/5, 5/3, 7/1, 1/8, 2/7, 4/5, 5/4, 7/2, 8/1, …
En esta entrada del Cuaderno de Cultura Científica hemos visto ejemplos de conjuntos numerables, que tienen la misma cantidad de elementos que el conjunto de los números naturales. En la siguiente entrada veremos, entre otras cosas, que existen conjuntos infinitos no numerables, como el conjunto de los números reales, como demostró el matemático ruso-alemán George Cantor, demostrando que existen más de un infinito.

Bibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – FESPM, 2021.
2.- David Foster Wallace, Todo y más, Breve historia del infinito, RBA, 2013.
3.- J. Stillwell, The Real Numbers: An Introduction to Set Theory and Analysis,
Undergraduate Texts in Mathematics, Springer, 2013.
4.- Eli Maor, To infinity and Beyond, A Cultural History of Infinity, Birkhauser, 1987.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El infinito en un segmento (3) — Cuaderno de Cultura Científica
[…] primera entrega de esta miniserie, El infinito en un segmento (1), se centró en cómo resolvió el matemático ruso-alemán el problema de comparar dos conjuntos […]
Omar Arturo Alvarez Zaleta
Muy bien explicado, lo del infinito, la correspondencia uno a uno ,