Con la entrada El infinito en un segmento (1) iniciábamos una pequeña serie de entradas, en el Cuaderno de Cultura Científica, sobre el concepto de infinito y la revolución que se produjo, a finales del siglo XIX, de la mano del matemático ruso-alemán George Cantor, quien demostró, entre otras cuestiones, que existía más de un infinito o que la cantidad de puntos de un segmento es la misma que la de un cuadrado.

En esa primera entrega nos planteábamos cómo comparar dos conjuntos infinitos, es decir, cuándo podemos decir que tienen la misma cantidad de elementos. La respuesta es sencilla y está, como mostramos, en la base del origen del concepto de número. Dos conjuntos tienen la misma cantidad de elementos cuando se puede establecer una “correspondencia uno-a-uno” entre los elementos de los dos conjuntos. Bajo esta mirada demostramos, como lo hizo Cantor, que el conjunto de los números racionales, aquellos números que se expresan como cociente a / b de dos números enteros a y b, es un conjunto infinito que tiene la misma cantidad de elementos que el conjunto de los números naturales, es decir, es un conjunto numerable (se puede “contar”, aunque no terminaremos nunca).

Las ciudades invisibles de Italo Calvino

Antes de seguir con las matemáticas del infinito, vamos a mostrar un hermoso ejemplo de la presencia de la demostración de la numerabilidad del conjunto de los números racionales en la cultura. Ya citamos en la anterior entrada, en relación con el infinito, la novela Maniac (2023), del escritor chileno Benjamín Labatut, la novela gráfica Las calles de arena (2009), del historietista valenciano Paco Roca, el relato El libro de arena del escritor argentino Jorge Luis Borges o la novela gráfica Última lección en Gotinga, del informático e historietista italiano Davide Osenda. En esta ocasión, nos referimos a la magnífica novela Las ciudades invisibles (1978) del escritor italiano Italo Calvino (1923-1985). Si no la has leído, este es un buen momento para leerla, tan bueno como cualquier otro, pero cuanto antes mejor.

En la sinopsis de este libro puede leerse lo siguiente, escrito por Italo Calvino.

Las ciudades invisibles se presentan como una serie de relatos de viaje que Marco Polo hace a Kublai Kan, emperador de los tártaros… A este emperador melancólico que ha comprendido que su ilimitado poder poco cuenta en un mundo que marcha hacia la ruina, un viajero imaginario le habla de ciudades imposibles, por ejemplo, una ciudad microscópica que va ensanchándose y termina formada por muchas ciudades concéntricas en expansión, una ciudad telaraña suspendida sobre un abismo, o una ciudad bidimensional como Moriana… Creo que lo que el libro evoca no es sólo una idea atemporal de la ciudad, sino que desarrolla, de manera unas veces implícita y otras explícita, una discusión sobre la ciudad moderna… Creo haber escrito algo como un último poema de amor a las ciudades, cuando es cada vez más difícil vivirlas como ciudades.

Es un libro muy conectado con las matemáticas, como demostró el matemático catalán Miquel Albertí Palmer, en una serie de diez maravillosos artículos publicados en la revista SUMA, de la Federación Española de Sociedades de Profesores de Matemáticas – FESPM. Estos pueden encontrarse en formato pdf en la página de la FESPM.

De todas las cuestiones de este libro relacionadas con las matemáticas, en esta entrada nos interesa su estructura, que tiene que ver con una forma diagonal de contar los números racionales, es decir, de demostrar que este es un conjunto numerable (con la misma cantidad de elementos que el conjunto de los números naturales).

En la nota preliminar para la edición de Siruela, basada en el texto inédito de una conferencia pronunciada por Italo Calvino en la Universidad de Columbia (Nueva York, EE.UU.) en 1983, dice lo siguiente respecto a la estructura del libro.

A partir del material que había acumulado fue como estudié la estructura más adecuada, porque quería que estas series se alternaran, se entretejieran, y al mismo tiempo no quería que el recorrido del libro se apartase demasiado del orden cronológico en que se habían escrito los textos. Al final decidí que habría 11 series de 5 textos cada una, reagrupados en capítulos formados por fragmentos de series diferentes que tuvieran cierto clima común. El sistema con arreglo al cual se alternan las series es de lo más simple, aunque hay quien lo ha estudiado mucho para explicarlo.

Para ver la estructura del libro, la forma en la que Italo Calvino ha ordenado los textos de esas “11 series de 5 textos cada una”, veamos el índice, que he incluido en la siguiente imagen.

Si nos fijamos bien, las once series de textos/ciudades son las siguientes.

1. Las ciudades y la memoria

2. Las ciudades y el deseo

3. Las ciudades y los signos

4. Las ciudades sutiles

5. Las ciudades y los intercambios

6. Las ciudades y los ojos

7. Las ciudades y el nombre

8. Las ciudades y los muertos

9. Las ciudades y el cielo

10. Las ciudades continuas

11. Las ciudades escondidas

Por ejemplo, las cinco ciudades de la serie 1 (las ciudades y la memoria) son Diomira, Isidora, Zaira, Zora y Maurilia, las cinco ciudades de la serie 2 (las ciudades y el deseo) son Dorotea, Anastasia, Despina, Fedora y Zobeida, o las cinco ciudades de la serie 11 (las ciudades escondidas) son Olina, Raísa, Marozia, Teodora y Berenice, por mencionar algunas.

Si utilizamos el número anterior, del 1 al 11, para determinar la serie, y un número, del 1 al 5, para determinar las cinco ciudades de cada serie, como aparecen en el índice, tenemos que los textos/ciudades que aparecen en cada uno de los nueve capítulos (denotados de la forma a/b, siendo a la serie y b el número de texto/ciudad en dicha serie) son los siguientes.

Capítulo I: 1/1; 1/2; 2/1; 1/3; 2/2; 3/1; 1/4; 2/3; 3/2; 4/1

Capítulo II: 1/5; 2/4; 3/3; 4/2; 5/1

Capítulo III: 2/5; 3/4; 4/3; 5/2; 6/1

Capítulo IV: 3/5; 4/4; 5/3; 6/2; 7/1

Capítulo V: 4/5; 5/4; 6/3; 7/2; 8/1

Capítulo VI: 5/5; 6/4; 7/3; 8/2; 9/1

Capítulo VII: 6/5; 7/4; 8/3; 9/2; 10/1

Capítulo VIII: 7/5; 8/4; 9/3; 10/2; 11/1

Capítulo IX: 8/5; 9/4; 10/3; 11/2; 9/5; 10/4; 11/3; 10/5; 11/4; 11/5

Visto de esta manera quizás podamos darnos cuenta del orden que se ha seguido, pero si construimos una retícula con las notaciones a/b (de las ciudades de las series), de manera que a coincida con la fila y b con la columna (aquí está cambiado el juego de filas y columnas respecto a la entrada anterior, con los números racionales), entonces el orden de presentación de los textos en el libro es el siguiente.

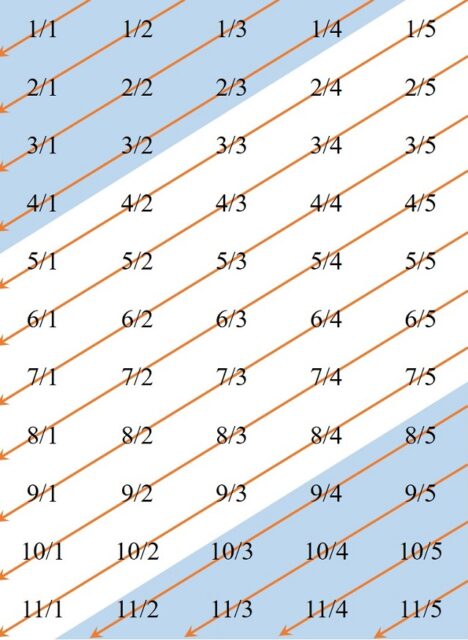
Como vemos el orden de recorrido es diagonal descendente y en cada capítulo están las cinco ciudades de una única diagonal, salvo el primero y el último que implican a cuatro pequeñas diagonales, con diez ciudades cada capítulo (igual a la suma de las ciudades/textos de cada diagonal, 1 + 2 + 3 + 4 = 10).

Si nos fijamos, en cada diagonal, la suma del número de fila a con el número de columna b, a + b, es la misma, luego el recorrido va aumentando, desde 1 en adelante, según el valor de dicha suma, y se recorre cada diagonal en el orden de crecimiento del valor de la fila a. Luego el recorrido es, como está mostrado arriba por capítulos, es decir, de la siguiente forma (he utilizado la negrita de forma alterna para destacar los cocientes a/b, que son las ciudades, de cada diagonal):

1/1; 1/2; 2/1; 1/3; 2/2; 3/1; 1/4; 2/3; 3/2; 4/1; 1/5; 2/4; 3/3; 4/2; 5/1; 2/5; 3/4; 4/3; 5/2; 6/1; 3/5; 4/4; 5/3; 6/2; 7/1; 4/5; 5/4; 6/3; 7/2; 8/1; 5/5; 6/4; 7/3; 8/2; 9/1; 6/5; 7/4; 8/3; 9/2; 10/1; 7/5; 8/4; 9/3; 10/2; 11/1; 8/5; 9/4; 10/3; 11/2; 9/5; 10/4; 11/3; 10/5; 11/4; 11/5.

Más aún, si nos fijamos bien, está relacionado con la segunda forma de contar los números racionales que mostramos en la anterior entrada, El infinito en un segmento (1), pero dejémoslo aquí y sigamos analizando conjuntos infinitos de números, para descubrir que existe más de un infinito, el revolucionario resultado de Cantor.

Los números reales, existe más de un infinito

En nuestro recorrido por las diferentes familias de números (naturales, enteros, racionales), la siguiente es la formada por los números reales, que incluye a los números racionales, más otros números denominados irracionales, ya que no pueden ser expresados como cociente de dos números enteros, como los números raíz cuadrada de 2, raíz cuadrada de 3, raíz cúbica de 5, el número pi, el número de oro (phi) o el número e, por ejemplo. En la entrada El asesinato de Pitágoras, historia y matemáticas (y II) podéis ver una sencilla demostración de la irracionalidad de la raíz cuadrada de 2.

En la siguiente imagen mostramos las diferentes familias de números que hemos ido considerando hasta el momento, con sus relaciones de inclusión (naturales, enteros, racionales, irracionales y reales).

Si consideramos la representación decimal de los números reales, cada número real está compuesto por una parte entera, a la izquierda de la coma, y una parte “decimal”, a la derecha, como en los siguientes ejemplos.

Si solo tiene parte entera, es decir, no hay números detrás de la coma (luego esta no se escribe) los números son enteros, como los dos primeros (3.579 y – 56); si la parte decimal es finita, como en el caso de 17/4 = 4,25, o infinita periódica, como en el caso de 1/7 = 0,142857142857… (con período 142857, que se repite de forma infinita) y 5/12 = 0, 416666666… (con período 6, despues de dos decimales, que se repite de forma infinita), entonces los números son racionales; mientras que si la parte decimal es infinita, pero no periódica, como en los casos del número raíz cuadrada de dos √2 y el número pi, cuyos decimales se extienden sin fin, pero sin ningún patrón periódico, entonces los números son irracionales. De esta forma podemos identificar a los diferentes números reales en función de su expresión decimal.

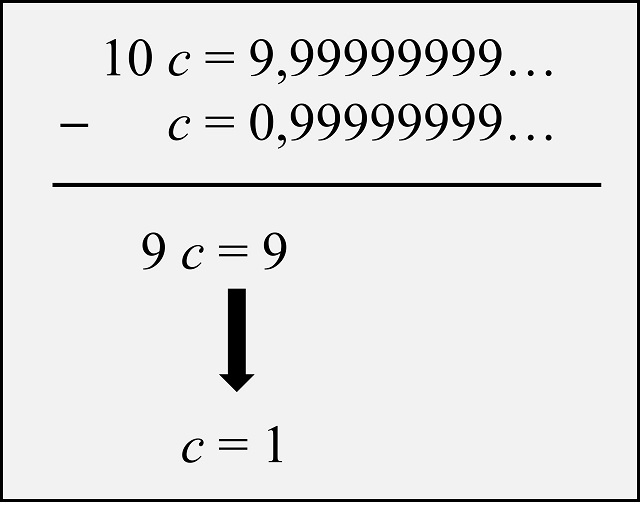
Aunque existe un pequeño contratiempo en relación a la representación decimal de los números reales y es que los números racionales con una cantidad finita (incluido el caso en el que esta es cero) de decimales su expresión decimal no es única, poseen dos expresiones decimales distintas. Por ejemplo, el número 1 (que no tiene parte decimal o podemos considerar que los decimales son todo ceros, 1,00000000…) se puede expresar también como 0,99999999…, o el número 4,25 (con dos decimales solamente, aunque podemos considerar que se sigue de infinitos ceros 4,2500000000…) se puede expresar como 4,2499999999… Para las cuestiones de las que vamos a hablar en el resto de esta entrada, donde vamos a identificar a los números reales mediante su expresión decimal, y sería deseable que esta sea única, consideraremos únicamente, como así lo consideró también Cantor, una de las dos expresiones anteriores, en concreto, la expresión con infinitos decimales en la que se repite el 9 de forma infinita.

Por si alguna de las personas que está leyendo esto no está familiarizada con esta cuestión, vamos a realizar la clásica prueba de que 0,99999999… es igual a 1. Llamemos c al número 0,99999999…, multipliquemoslo por 10, es decir, 10 c = 9,99999999… y restemos ambas cantidades, entonces nos queda que 9 c = 9, luego c = 1, y queda demostrado.

El resultado de Cantor

Ya estamos en condiciones de presentar el revolucionario resultado de George Cantor que conmocionó a la comunidad matemática de finales del siglo xix, que existen más de un infinito. Este resultado fue demostrado por George Cantor en su artículo Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen / Sobre una propiedad de la colección de todos los números algebraicos reales, publicado en 1874, en la revista alemana de investigación matemática Journal für die Reine und Angewandte Mathematik (conocida como la Revista de Crelle, por ser el matemático alemán August Leopold Crelle (1780-1855) quien la fundó). En esta entrada vamos a utilizar el conocido argumento diagonal de Cantor, que no es el original del artículo de 1874, más complejo, sino el argumento que presentó en un artículo posterior de 1891 (Über eine elementare Frage der Mannigfaltigskeitslehre / Sobre una cuestión elemental de la teoría de la multiplicidad), para demostrar que en el intervalo (0,1), es decir, los números reales mayores que 0, pero menores que 1, que son aquellos cuya expresión decimal posee un 0 en la parte entera, no es numerable, esto es, posee más elementos que el conjunto de los números naturales. Por lo tanto, existen, al menos, dos infinitos diferentes, el de los números naturales y el de los números reales (de hecho, la cantidad de números reales es la misma que la cantidad de números reales del intervalo (0,1), cuya prueba no es muy complicada, pero la dejamos para otro momento).

El argumento diagonal de Cantor es el siguiente. Supongamos que el intervalo (0,1) fuese numerable, es decir, que se pudiera establecer una correspondencia uno-a-uno entre el conjunto de los números naturales y el conjunto de los números reales del intervalo (0,1). Entonces podríamos numerar todos los números reales entre 0 y 1, cuyo listado podría empezar como aparece en la siguiente imagen (ojo, hemos puesto un ejemplo concreto en lugar de una expresión genérica, para facilitar la comprensión).

En tal caso, se va a poder construir un número real del intervalo (0,1) que no está en el anterior listado infinito, en contradicción con la hipótesis, que establece que existe una correspondencia uno-a-uno entre el conjunto de los números naturales y el de los números reales del intervalo (0,1). Por lo tanto, el infinito de los números reales sería mayor que el infinito de los números naturales.

Veamos cómo construir ese nuevo número que no estaría listado en la anterior correspondencia entre números naturales y números reales del intervalo (0,1). Primero, nuestro número real tendría al 0 en la parte entera, ya que es un número real entre 0 y 1. Para decidir quien va a ser su primer decimal, miramos al número real que está en la posición 1 (es la imagen del 1 mediante la correspondencia uno-a-uno), que en este caso es 0,𝟏23456789…, y como el primer decimal de este es el 1, tomamos cualquier cifra (de las diez cifras básicas, 1, 2, 3, …, 8, 9, 0) distinta de 1, por ejemplo, 2, luego nuestro número empieza por 0,2. Para decidir el segundo decimal, miramos al número real de la posición 2, que es 0,2𝟏2121212… y miramos a su segundo decimal, que es 1, por lo que tomamos cualquier cifra distinta de esta, por ejemplo, 2, luego el número que estamos construyendo seguiría 0,22. Para el tercer decimal, miramos al tercer número del listado, 0,19𝟗999999…, y a su tercer dígito, que es 9, por lo que elegimos uno diferente a este, como el 0, por lo que continuamos con el número 0,220. Para el cuarto decimal nos fijamos en el cuarto decimal del cuarto número, 0,989𝟖98989…, que es 8 y tomamos una cifra diferente, por ejemplo, 9, por lo que seguimos 0,2209. Y así se continúa con cada posición decimal. Para la posición decimal k del número que estamos construyendo, miramos al número que está en la posición k del listado y a la posición decimal k-ésima del mismo, parta tomar una cifra diferente a ella. Por ejemplo, en nuestro caso el número podría ser (sus primeros dígitos):

0,220928101…

Por la construcción de este número, no puede estar en el listado anterior, que se suponía que recorría todos los números reales entre 0 y 1. No puede ser el primer número del listado, ya que su primer decimal (2) no coincide con el primer decimal del primer número de la lista (1); no puede ser el segundo número, ya que su segundo decimal (2), no coincide con el del segundo (1); no puede ser el tercero, ya que su tercer decimal (0), no coincide con el del tercero de la lista (9); y, en general, no va a poder ser el número que está en la posición k del listado, ya que hemos construido nuestro número para que los decimales en la posición k de ambos no coincidan.

Teorema (Cantor, 1874): El conjunto de los números reales es no numerable.

Corolario (Cantor, 1874): Existe más de un infinito, al menos, el infinito de los números naturales (cuyo cardinal se denomina aleph-zero) y el infinito de los números reales (cuyo cardinal se denomina cardinal del continuo, c).

El infinito en un cuadrado

Una vez demostrado que el cardinal del continuo c (el infinito de los números reales) es mayor que aleph-zero (el infinito de los números naturales), George Cantor se planteó, como puede observarse en su correspondencia con su colega, el matemático alemán Richard Dedekind (1831-1916), si el plano (dimensión 2) tiene una mayor cantidad de puntos que la recta (dimensión 1), es decir, si el infinito del plano es mayor que el infinito del continuo. Simplificando la cuestión.

Problema: ¿Hay la misma cantidad de puntos en el segmento unidad (0,1) que en el cuadrado unidad (0,1) x (0,1)?

En la siguiente entrada, la última de la serie El infinito en un segmento, abordaremos esta cuestión, que fue la que motivó que Cantor le escribiera a su colega Dedekind “Je le vois, mais je ne le crois pas” (en francés en el original, aunque la carta estaba escrita en alemán), es decir, “Lo veo, pero no lo creo”, tras la demostración de que el segmento y el cuadrado tienen la misma cantidad de puntos, en contra de lo que podría sugerirnos nuestra intuición.

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – FESPM, 2021.

2.- David Foster Wallace, Todo y más, Breve historia del infinito, RBA, 2013.

3.- J. Stillwell, The Real Numbers: An Introduction to Set Theory and Analysis, Undergraduate Texts in Mathematics, Springer, 2013.

4.- Eli Maor, To infinity and Beyond, A Cultural History of Infinity, Birkhauser, 1987.

5.- José A. Prado-Bassas, Historia del infinito (el apasionante relato de uno de los conceptos más profundos y enigmáticos de las matemáticas), Pinolia, 2023.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica