Esta es la última jornada de un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci. Durante la primera jornada, recogida en la entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I), visitamos espacios destacados como el árbol genealógico de un zángano (abeja macho), los paseos de una abeja por un panal de dos filas de celdas o los embaldosados con fichas de dominó, mientras que para la segunda jornada, Fibonacci en todas partes (II), reservamos la visita a lugares de interés como la óptica de la luz, unas escaleras que se suben, o se bajan, de una en una o de dos en dos, y las sumas de números con unos y doses.

Pintando un edificio de apartamentos
Con el problema de pintar un edificio de apartamentos con dos colores distintos iniciamos la tercera jornada de este paseo. El enunciado de este clásico problema dice así.
Problema: Si un edificio de apartamentos de n plantas va a ser pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, ¿de cuántas formas es posible hacerlo?
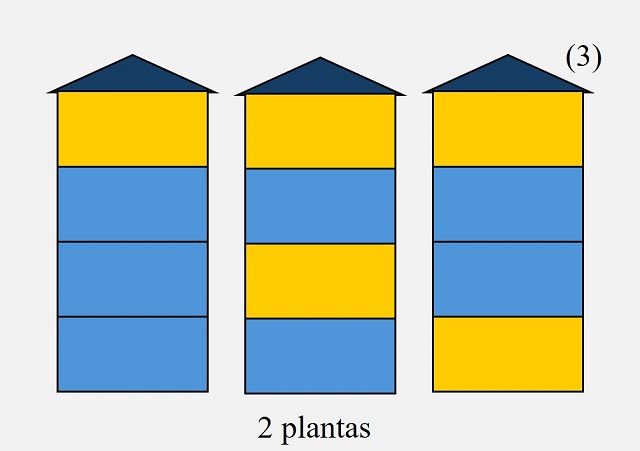
Para resolver este problema, podemos empezar de forma experimental, viendo qué ocurre para los edificios con un número pequeño de plantas. Para un edificio de apartamentos con una sola planta, existen solo dos opciones (2), pintar esa única planta de azul o de amarillo. Para dos plantas, hay tres opciones (3), pintar las dos plantas de azul, ambas de amarillo no es posible, o pintar cada planta de un color, lo cual se puede hacer de dos formas distintas, como se observa en la siguiente imagen. Mientras que para un edificio de tres plantas pueden pintarse todas de azul, puede pintarse una de amarillo, que puede ser la primera, la segunda o la tercera planta, o pueden pintarse dos plantas de amarillo, que por la condición de que no haya plantas amarillas contiguas, solo puede hacerse de una manera, en las plantas de los extremos, en total cinco formas distintas (5).
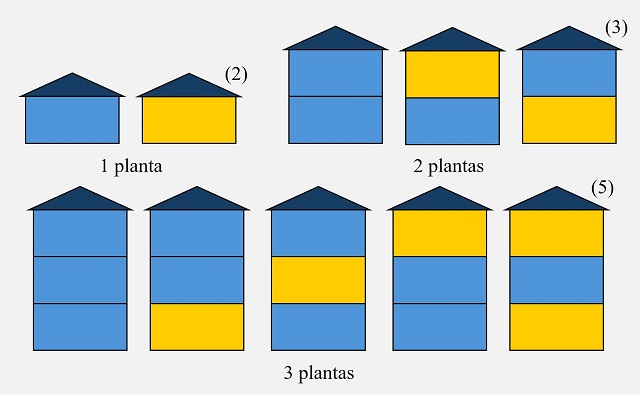
Si ahora consideramos un edificio de cuatro plantas, puede pintarse todo de azul, con una planta amarilla y hay cuatro plantas, o con dos plantas amarillas, que puede hacerse de tres formas diferentes sin que coincidan de amarillo plantas adyacentes, pero no es posible que tres o cuatro plantas estén pintadas de amarillo. En total, hay ocho (8) maneras de pintar el edificio de apartamentos.
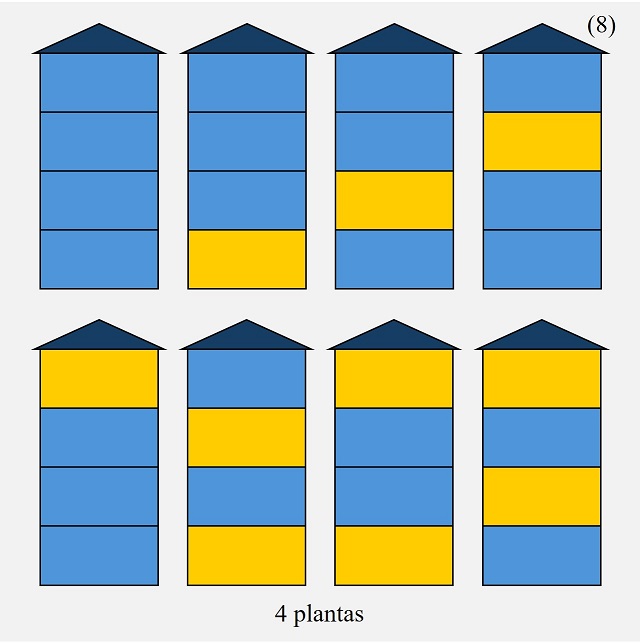
Como observamos los números que nos salen son 2, 3, 5 y 8, que son números de la sucesión de Fibonacci. Veamos que es la sucesión de Fibonacci, empezando en 2 y 3, viendo que satisface la condición recursiva, que la cantidad de maneras de pintar un edificio de n plantas se puede obtener a partir de las de n – 1 y n – 2 plantas. Para ello, observemos qué ocurre con el caso de n = 4 (cuatro plantas).
Si tomamos los edificios de 3 plantas (n – 1, en general) y consideramos una planta más, por encima de las otras, pintada de azul, generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 3 plantas (n – 1 plantas en general), que son 5 maneras distintas. Observemos que no podemos pintar de amarillo en todos los casos puesto que en algunos la última planta está pintada de amarillo, por lo que coincidirían dos plantas amarillas, mientras que los casos en los que la última planta es azul, aunque sí podríamos pintar la siguiente de amarillo, ese caso va a estar considerado en los casos que se derivan del edificio de n – 2 plantas (2 plantas en nuestro ejemplo), que veremos a continuación. Recíprocamente, si tomamos las maneras de pintar un edificio de 4 plantas (n, en general) en las cuales su última planta es azul, son todas las de 3 plantas (n – 1), a las que le añadimos una última planta azul.
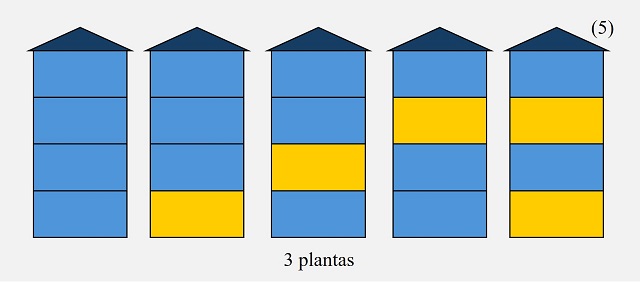
Si tomamos los edificios de 2 plantas (n – 2, en general) y consideramos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo), generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 2 plantas (n – 2 plantas en general), que son 3 maneras distintas. Observemos que no podríamos pedir pintar esas dos plantas superiores de azul y amarillo, ya que podrían coincidir dos plantas adyacentes amarillas, además los casos en los que sí se pueda, ya que la última planta de las anteriores es azul, ya está considerado en el caso anterior. Más aún, así cubrimos todos los casos de un edificio de 4 plantas (n, en general) en las cuales su última planta es amarilla.
En consecuencia, hemos demostrado que se cumple la misma propiedad recursiva que para la sucesión de Fibonacci, Fn = Fn – 1 + Fn – 2. Por lo tanto, el número de formas distintas de pintar un edificio de apartamentos de n plantas, pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, es Fn + 2.
Palabras de n-bits
Empecemos por lo elemental. Una palabra de n-bits es una cadena de n bits, donde un bit –acrónimo de bi[nary digi]t / dígito binario– es la unidad mínima de información y se corresponde con un dígito del sistema de numeración binario, 0 ó 1. Así, 1001001 sería una palabra de 7-bits o 1010101110110 una palabra de 13-bits.
Si lo pensamos un momento, resulta que la cuestión anterior de pintar de dos colores (azul y amarillo) un edificio de n plantas es equivalente al siguiente resultado.
Teorema: El número de palabras de n-bits que no contengan dos 1s consecutivos es igual a Fn + 2.
Veamos en la siguiente tabla, las palabras de n-bits para longitudes n pequeñas.
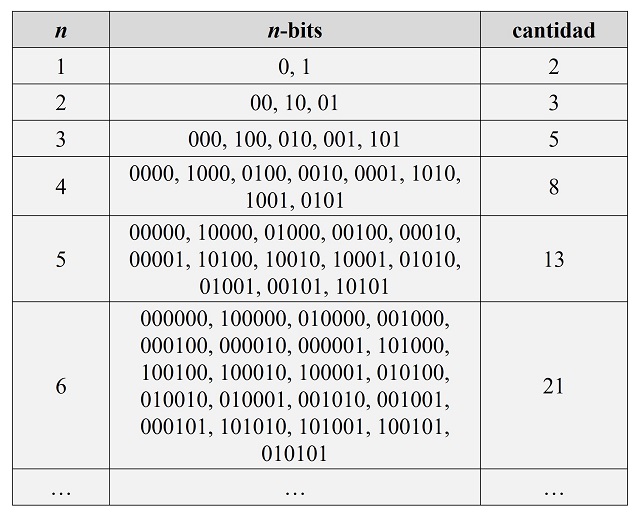
La demostración del teorema anterior es la misma que la de las maneras de pintar un edificio. Si se consideran las palabras de n-bits, las que terminan en 1 (por la derecha) son las palabras de (n – 1)-bits a las que se les añade un 1 por la derecha, mientras que las palabras que terminan en 0 son las palabras de (n – 2)-bits a las que se les añade 10 por la derecha.
Lanzar una moneda
Llegados a este punto del paseo, nos podemos plantear una visita extra a un lugar que es un problema de probabilidad.
Problema: Si lanzamos una moneda n veces (sea n la cantidad que queramos), ¿cuál es la probabilidad de que no haya dos lanzamientos adyacentes que sean ambos cara?
Empecemos recordando que la probabilidad de que un evento ocurra se calcula dividiendo “el número de casos favorables” entre “el número de casos posibles” (pueden leerse las entradas relacionadas con la probabilidad, La probabilidad en el banquillo de los acusados o El cuento de la ruleta rusa ). Así, dada una determinada familia con dos “hijos”, si nos preguntamos cuál es la probabilidad de que los dos sean chicas, tendríamos que calcular primero el espacio muestral, es decir, el espacio de todos los casos posibles. En esta ocasión, habrá cuatro posibles casos (chica, chica), (chica, chico), (chico, chica) y (chico, chico), donde el orden en el par expresa el orden cronológico de nacimiento. Como solo uno de los cuatro es favorable, son dos chicas, la probabilidad de que los dos “hijos” sean chicas es 1/4 = 0,25, es decir, una probabilidad del 25%.

Para analizar nuestro problema, si lanzamos una moneda al aire puede salir cara (que vamos expresarlo, para simplificar, pero también para disponer de una notación simple, con un 1) o puede salir cruz (que lo expresaremos con un 0). De esta manera, si lanzamos una moneda n veces, la representación de un posible resultado es un n-bit. Por ejemplo, si hablamos de lanzar la moneda 5 veces, entonces 10011 representa la posibilidad de que salga cara / cruz / cruz / cara / cara, mientras que 00101 sería cruz / cruz / cara / cruz / cara.
Por lo tanto, ya estamos en condiciones de calcular la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara. En primer lugar, calculemos el número de casos posibles. Estos son, teniendo en cuenta la descripción anterior de los posibles lanzamientos, todas las palabras de n-bits, que son 2n, ya que cada vez que lanzamos la moneda hay dos posibilidades, cara (1) o cruz (0), en un total de n lanzamientos. Y ahora toca calcular el número de los casos posibles, que, por la descripción anterior, son las palabras de n-bits para las que no hay dos 1s consecutivos, que ya hemos calculado y que es igual al número de Fibonacci Fn + 2.
Por lo tanto, la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara, es igual a:
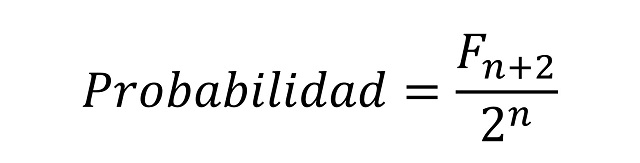
Por ejemplo, si lanzamos una moneda 5 veces, la probabilidad de que no haya dos lanzamientos consecutivos que sean cara es 13 / 32 = 0,40625, es decir, un 40,625 por ciento. Si vamos realizando cada vez más lanzamientos, nos podemos plantear si esa probabilidad aumenta o disminuye. Si lo pensamos un poco, intuitivamente es bastante claro que esa probabilidad irá disminuyendo, ya que con más lanzamientos será más fácil que salgan dos caras seguidas. Veamos qué pasa con las primeras cantidades de lanzamientos.
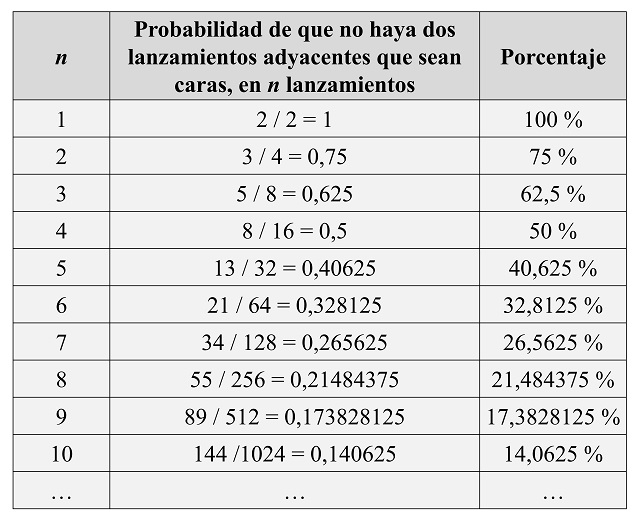
Efectivamente, la probabilidad va disminuyendo, como intuíamos. Esto se debe, matemáticamente, a que la sucesión de las potencias de 2 crece más rápido que la sucesión de los números de Fibonacci.
Subconjuntos alternados
Vamos a terminar este paseo con un problema propuesto por el matemático francés Olry Terquem (1782-1862), del que ya hablamos en la entrada La circunferencia de los nueve puntos.
Un subconjunto del conjunto {1, 2, 3, …, n – 1, n} se dice que es alternado si sus elementos, cuando se colocan en orden creciente, siguen el patrón impar, par, impar, par, etcétera. Por ejemplo, los conjuntos {4}, {3, 6} o {1, 2, 5, 6} son subconjuntos alternados de {1, 2, 3, 4, 5, 6}, mientras que {2, 4, 5} o {1, 2, 3, 5} no lo son. El problema que se planteó Terquem fue calcular el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1, n}. Veamos qué ocurre para los primeros casos.

Por lo tanto, el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1. n} es igual al número de Fibonacci Fn + 2.
Podemos llegar a la sucesión de Fibonacci de muchas otras maneras, pero esas os las dejo para quienes os animéis a indagar sobre este tema.

Bibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Demetrio Miguel
EXCELENTE TRABAJO.