En el libro El prodigio de los números, del divulgador científico estadounidense Clifford A. Pickover (1957) se muestra un rompecabezas geométrico, conocido con el nombre de IQ-Block, que está formado por piezas geométricas pertenecientes a la versátil familia de los poliominós. Vamos a dedicar esta entrada del Cuaderno de Cultura Científica a este juego geométrico.

El juego fue fabricado y comercializado por la empresa británica Hercules, aunque manufacturado en Hong-Kong, hacia la década de 1980.

Los poliominós, juntando cuadrados

Los poliominós son unos curiosos objetos geométricos que fueron introducidos formalmente por el matemático e ingeniero estadounidense Solomon W. Golomb (1932-2016) en una conferencia en el Harvard Mathematics Club en 1953, y en su posterior artículo Checkers Boards and Polyominoes publicado en la revista American Mathematical Monthly, revista matemática de la MAA (Asociación Matemática de América) dirigida a un amplio público dentro de las matemáticas, desde estudiantes de grado hasta investigadores punteros, que se ha convertido en la revista matemática más leída del mundo. Pero serían descubiertos para el público general por el gran divulgador de las matemáticas Martin Gardner (1914-2010), en su columna de juegos matemáticos de Scientific American (1957). Poco después, en 1965, Golomb publicaría un extenso libro que analizaba en profundidad estos objetos geométricos, con el sencillo título Polyominoes (Poliominós). Al introducir los poliominós, el matemático abrió un fructífero campo para las matemáticas, las ciencias de la computación y la creación de juegos. Están relacionados con conceptos matemáticos como las teselaciones (o embaldosados), los patrones geométricos, los empaquetamientos o la medida (área), y de ellos han surgido infinidad de juegos de ingenio y rompecabezas geométricos, como el juego de los pentominós y sus derivados (véase la entrada Tetris, embaldosados y demostraciones), el Tetris o el Vee-21 (véase la entrada Embaldosando con L-triominós (Un ejemplo de demostración por inducción)), por citar algunos.

Un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro. Si unimos dos cuadrados se obtiene un dominó, si se juntan tres cuadrados se construye un triominó, o trominó, con cuatro cuadrados se tiene un tetraminó, con cinco un pentominó, y así se puede continuar para cualquier número de cuadrados, hexaminó, heptaminó, octominó. etcétera. Podemos considerar que un único cuadrado es también un poliominó, que denominamos monominó.

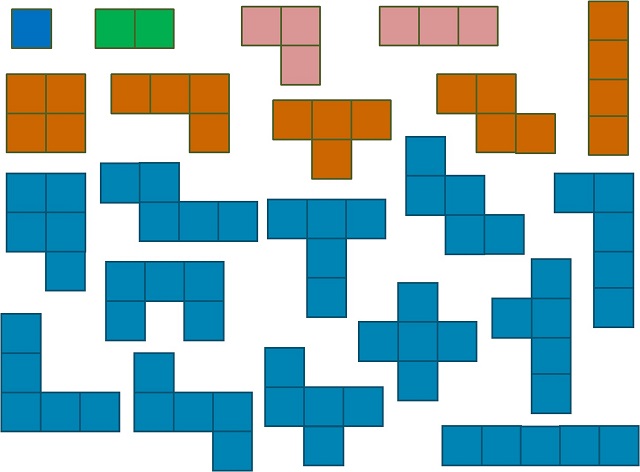
Como podemos ver en la anterior imagen, existen un monominó, un dominó, dos triominós, cinco tetraminós y doce pentominós. Si pasamos al orden seis, la familia de los poliominós se extiende con 35 hexominós, poliominós formados con seis cuadrados.

Antes de seguir adelante con el rompecabezas, una pequeña aclaración sobre estas piezas. Como estamos trabajando con piezas geométricas que vamos a poder manipular, se considera que podemos darles la vuelta, luego poliominós como los de la imagen (que son dos tetraminós) se consideran iguales, ya que dando la vuelta a uno se obtiene el otro (que es su imagen especular). Si estuviésemos trabajando con juegos o cuestiones simplemente planas, con en el Tetris, serían poliominós distintos, en cuyo caso podríamos hablar de “poliominós planos” o “poliominós de una cara”, como los denomina Golomb. Por ejemplo, hay 5 tetraminós (poliominós construidos con cinco cuadrados), como se muestra en la imagen de arriba, pero existen siete si hablamos de poliominós de una cara.

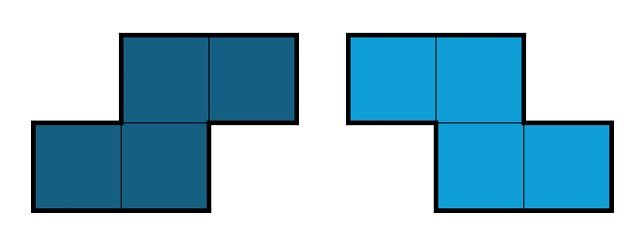
Aunque para lo que nos ocupa en esta entrada del Cuaderno de Cultura Científica seguiremos con los poliominós normales, los que se pueden voltear.

Las piezas del rompecabezas IQ-Block

Este rompecabezas geométrico está formado por diez piezas, diez poliominós, en concreto, un tetraminó, dos pentominós, dos hexominós, dos heptominós y tres octominós, una de ellas con forma de rectángulo, otra con forma de Z y las demás con formas que son, más o menos, una L, como aparece en la siguiente imagen.

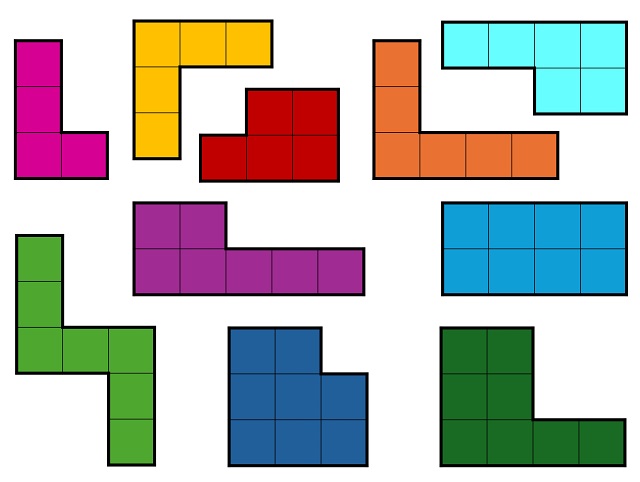
El número total de cuadrados implicados en las diez piezas del juego son 64 (1 x 4 + 2 x 5 + 2 x 6 + 2 x 7 + 3 x 8), luego, a priori, se podría, y se puede, formar un cuadrado de lado 8, como se muestra en la siguiente imagen.

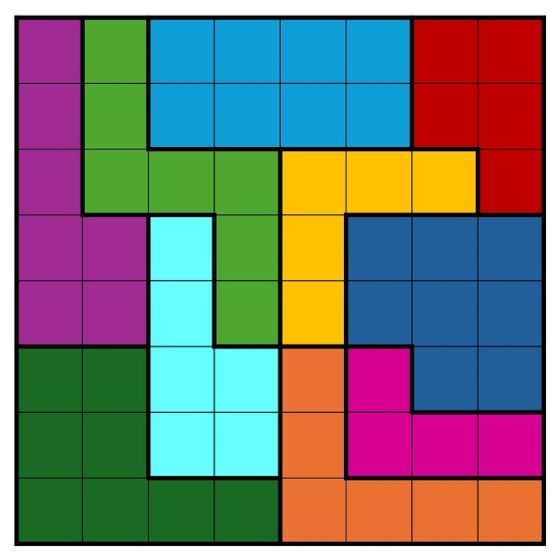
Este es esencialmente el objetivo de este rompecabezas, construir un cuadrado grande 8 x 8, un cuadrado de lado 8, es decir, formado por 64 cuadrados, con las diez piezas del juego. Tengamos en cuenta que las piezas del rompecabezas se pueden rotar y dar la vuelta.

Antes de seguir adelante, mi recomendación es construirse uno mismo las piezas de este rompecabezas, ya sea con papel, cartulina, papel maché, madera o piezas de algún juego de construcción, como he hecho yo, que he utilizado piezas cuadradas del LiveCube, para poder disfrutar jugando con las mismas, tanto mientras se lee esta entrada, como después.

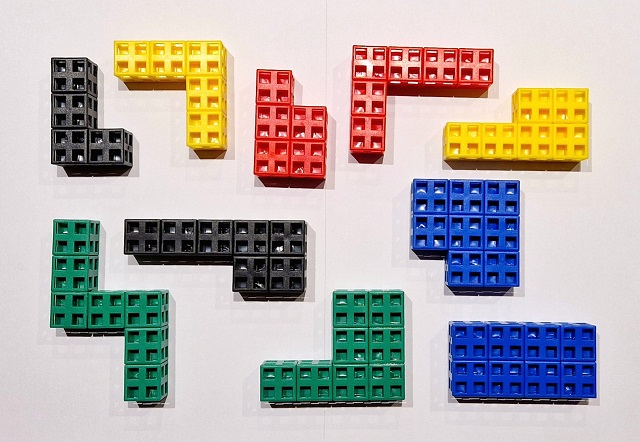
El rompecabezas IQ-Block

Como acabamos de comentar, el objetivo de este rompecabezas es formar un cuadrado grande 8 x 8 con las diez piezas que acabamos de describir, un tetraminó, dos pentominós, dos hexominós, dos heptominós y tres octominós.

Aunque, en el juego comercializado por la empresa Hercules las reglas del rompecabezas estaban escritas de la siguiente forma.

Primero debes elegir una de las piezas del juego, la que desees, que es la que va a estar colocada en la esquina superior izquierda (véase imagen inferior). Después, coloca las otras nueve piezas para que formen un cuadrado 8 x 8, sin mover de la esquina superior izquierda la pieza elegida.

Como vemos el objetivo del juego es formar un cuadrado grande de tamaño 8 x 8, con las diez fichas del juego, aunque en las reglas del juego comercial se plantea que se obtenga al menos una solución para cada una de las fichas colocada en la esquina superior izquierda. Por una parte, se amplia el reto a encontrar al menos diez soluciones, una por cada una de las diez fichas colocadas en la esquina. Pero además si se tiene en cuenta que cada ficha elegida para la posición de la esquina superior izquierda puede ser colocada de varias maneras distintas, se puede buscar al menos una solución para cada ficha y para cada una de sus posiciones posibles en la esquina superior izquierda. Quizás, este es el motivo por el cual en las reglas se menciona que hay bastantes soluciones distintas, en concreto:

Existen más de sesenta soluciones distintas que puedes encontrar. Se muestran dos soluciones a modo de ejemplo.

Las dos soluciones mostradas en las reglas del juego comercial son las siguientes.

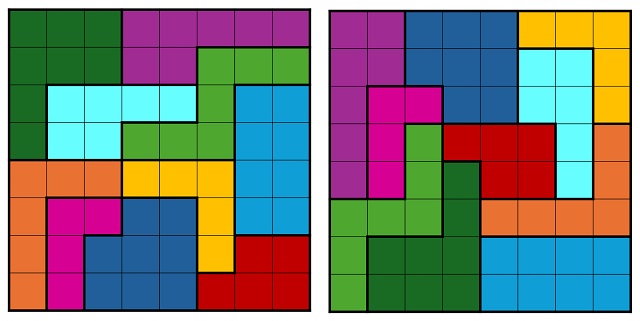
Es cierto que, al plantearse en las reglas del rompecabezas IQ-Block obtener soluciones para cada ficha, y para cada una de sus posiciones posibles, colocada en la esquina superior izquierda, esto nos anima a obtener muchas más soluciones, que solamente una, pero también a clasificarlas a la hora de encontrarlas, según cual sea la ficha y la posición de esa esquina.

Y la parte de las reglas del juego termina con la siguiente frase.

Trata de encontrar la mayor cantidad de soluciones posibles. Únete a nosotros para desafiar a tu I. Q. (Intelligence Quotient / Cociente intelectual).

Las soluciones del IQ-Block

Una pregunta lógica, tanto de quien idea y construye el rompecabezas, como de quien pretende solucionarlo, es cuántas soluciones distintas existen. En las reglas del juego afirman que existen más de 60 soluciones, pero no sabemos, al leer eso, cuántas más hay, es decir, cuántas son realmente todas las soluciones del rompecabezas.

Antes de seguir con esta cuestión observemos las dos soluciones que nos ofrecen como ejemplos en las reglas del juego. La primera de ellas es exactamente la misma que la que se había mostrado antes, pero girada 90 grados en el sentido de las agujas del reloj. Desde el punto de vista de las soluciones estas dos se consideran “esencialmente” la misma, al igual que las obtenidas si seguimos girando 90 grados, e incluso si diésemos la vuelta a la solución, luego todas ellas cuentan como una en el cómputo de soluciones.

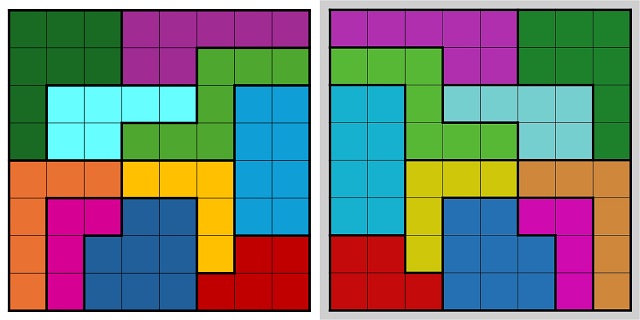
El matemático estadounidense Charles Ashbacher, que fue co-editor de la revista Journal of Recreational Mathematics, revista en la cual Pickover había publicado un par de artículos sobre el rompecabezas IQ-Block, escribió un programa de ordenador que rápidamente obtuvo mil soluciones distintas del rompecabezas. Sin embargo, hay más soluciones aún. El alemán Hartmut Blessing, miembro de MENSA e INTERTEL, sociedades de personas con alto cociente intelectual, afirma que existen 12.724 soluciones, lo cual ha sido comprobado con el programa PolySolver, que es un programa de Jaap Scherphuis que resuelve una gran variedad de rompecabezas geométricos.

Algunos retos con las piezas del IQ-Block

El autor de libros como El prodigio de los números (2000), La maravilla de los números (2001), Las matemáticas de Oz (2002), La banda de Moebius (2006), El libro de las matemáticas, de Pitágoras a la 57ª dimensión (2009) o Inteligencia artificial (2019), entre muchos otros, planteaba en su libro El prodigio de los números algunos retos relacionados con este rompecabezas.

Pregunta 1: ¿Puede construirse una estructura cuadrada eliminando una pieza y utilizando todas las restantes?

La respuesta a esta cuestión es sencilla. Al eliminar una pieza, que tendrá 5, 6, 7 u 8 cuadrados, nos quedarán nueve piezas que sumarán entre todas entre 56 y 59 cuadrados, lejos del siguiente número cuadrado más bajo 49 (que correspondería con un cuadrado 7 x 7), luego la respuesta es negativa.

Pero podemos ir un poco más allá, analizando caso por caso. Si se elimina la pieza con 5 cuadrados (pentominó) quedarían nueve piezas con 64 – 5 = 59 cuadrados, pero 59 es un número primo, luego es imposible formar una estructura rectangular, no solo cuadrada, con las nueve piezas restantes. Si se quita una de las dos piezas con 6 cuadrados (hexaminós) las otras nueve piezas sumarían 64 – 6 = 58, que es igual a 2 x 29, luego a priori podría formarse un rectángulo de tamaño 2 x 29, lo cual es imposible en este caso ya que hay varias piezas cuya anchura mínima es tres, luego imposible colocarlas para formar un cuadrado de anchura 2. Si se elimina una pieza de 7 cuadrados (heptominós), quedarían nueve piezas con 64 – 7 = 57, que es igual a 3 x 19, luego se podría construir un rectángulo de tamaño 3 x 19, lo cual es posible como he podido comprobar por mí mismo (si tenéis construidas las piezas del rompecabezas podéis buscar alguna distribución posible). Finalmente, si se deja fuera una pieza de 8 cuadrados quedan nueve piezas con 56 cuadrados en total, pero como 56 = 7 x 8, se podría formar un rectángulo de tamaño 7 x 8, lo cual es posible, como se muestra en la siguiente imagen.

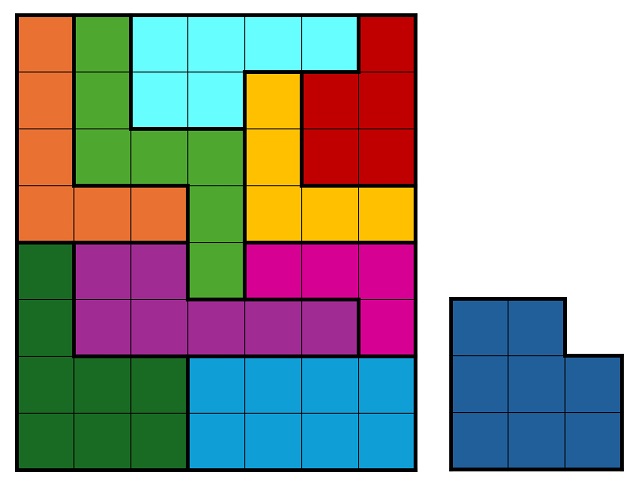
En este último caso, si se elimina una pieza de 8 cuadrados, ya hemos explicado que quedan nueve piezas con 56 cuadrados entre todas y se puede construir un rectángulo de tamaño 7 x 8, pero pensemos … ¿también se podría construir de tamaño 14 x 4? La respuesta a esta cuestión también la dejo para que la penséis quienes estáis leyendo esta entrada.

La cuestión anterior puede ampliarse a dos piezas (o más).

Pregunta 2: ¿Puede construirse una estructura cuadrada eliminando dos piezas y utilizando todas las restantes?

Como el siguiente número cuadrado, más pequeño que 64, es 49, como hemos comentado arriba, y la diferencia entre ambos es 64 – 49 = 15, hay que eliminar una pieza con 7 cuadrados y otra con 8, solo para esta opción podría ser posible construir una estructura cuadrada con el resto de piezas. Teniendo en cuenta esta información podéis buscar vosotros mismos dichas estructuras.

Si hasta ahora la diversión consistía en construir un cuadrado 8 x 8 (o más pequeños si se eliminan piezas), ahora vamos a darle la vuelta a la tortilla, ahora se tratará de formar, con las diez piezas del IQ-Block, el perímetro alrededor de un cuadrado 8 x 8, o si se elimina una pieza, un cuadrado 7 x 7.

Pregunta 3: ¿Puede construirse el perímetro de una estructura cuadrada vacía de tamaño 8 x 8 con todas las piezas del rompecabezas? ¿Y si se elimina una pieza puede construirse el perímetro de una estructura cuadrada vacía de tamaño 7 x 7?

Veamos una posible solución a la primera cuestión.

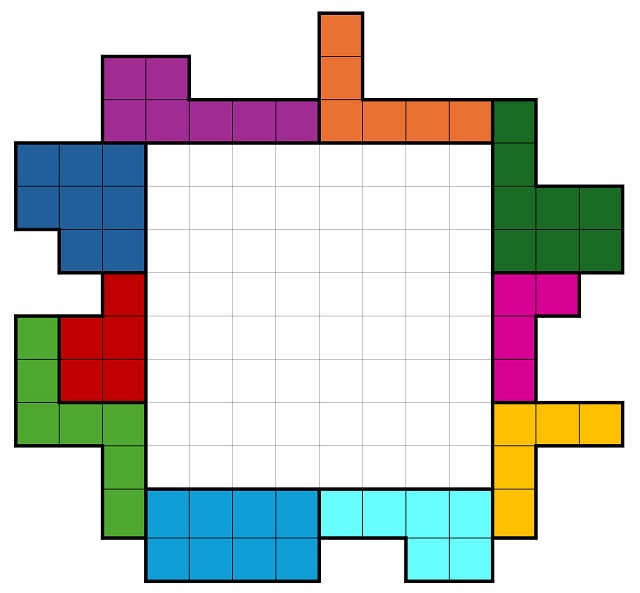
Dejo para diversión de las personas que estáis leyendo esta entrada la búsqueda de soluciones, que las hay, para el caso en el que se quita una de las piezas del rompecabezas y se utilizan las otras nueve piezas.

Bibliografía

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

2.- Solomon W. Golomb, Polyominoes: Puzzles, Patterns, Problems, and Packings, Princeton University Press, 1994.

3.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica