Sobre el interesante juego matemático que nos plantea Alicia con la tabla de multiplicar del cuatro
Durante la última edición de la Jornada BCAM-NAUKAS en el Día de Pi (Día Internacional de las Matemáticas), organizada el pasado 14 de marzo (de 2025) en el Bizkaia Aretoa (Bilbao) de la Universidad del País Vasco, estuve conversando con Fátima García Doval (autora de los libros La educación es otra historia. Usando la historia para comprender mejor la educación actual (2023) y Psicomitos. Una crítica a la psicología no científica (2024), y conocida en las redes sociales como “Minina de Cheshire”) sobre el famoso libro Alicia en el País de las Maravillas, el número 42, que recordemos es “la respuesta definitiva a la vida, el universo y todo lo demás” (según la novela La guía del autoestopista galáctico, del escritor inglés Douglas Adams) y las bases de numeración. En dicha conversación Fátima mencionó un hermoso pasaje de Alicia en el País de las Maravillas relacionado con las bases de numeración y que ella recordaba que podía tener relación con el número 42.
Al día siguiente me envió el siguiente fragmento de Alicia en el País de las Maravillas, por el cual le estoy profundamente agradecido. Aunque antes de mostraros el fragmento vamos a ponerlo en contexto. En el inicio del libro Las aventuras de Alicia en el País de las Maravillas (1865), que es realmente el título de esta novela de fantasía, su protagonista Alicia ve un curioso conejo blanco con chaleco y reloj de bolsillo al que oye decir “¡Dios mío! ¡Dios mío! ¡Voy a llegar demasiado tarde!” y sin pensárselo dos veces le sigue cuando este entra en su madriguera. Nada más entrar Alicia empieza a caer y sigue cayendo, y cayendo, hasta llegar a un extraño lugar, en el que empieza a vivir situaciones de lo más extravagantes, lo que le lleva a cuestionarse si no se habrá producido un cambio en ella esa noche y quizás sea una persona distinta. Entonces, piensa lo siguiente:
Desde luego, no soy Ada –dijo-, porque ella lleva largos tirabuzones, y yo no tengo ningún tirabuzón; ¡y desde luego no puedo ser Mabel, porque yo sé toda clase de cosas y ella, en cambio, sabe poquísimo! Además, ella es ella, y yo soy yo, y … ¡ay, Dios, qué lioso es todo esto! Probaré a ver si sé todas las cosas que solía saber. Vamos a ver: cuatro por cinco son doce; cuatro por seis, trece; cuatro por siete … ¡Dios mío, de esta manera no llegaré nunca a veinte! De todos modos, la Tabla de Multiplicar no tiene importancia; probemos con la Geografía.

Junto con el anterior fragmento Fátima incluía el siguiente apunte, “4 x 5 es 12 en base 18 y 4 x 6 es 13 en base 21”. Como podéis imaginar rápidamente me dispuse a hacer las demás cuentas, ya que el propio Lewis Carroll nos animaba a ello al dejar en el aire la multiplicación 4 x 7, es decir, nos animaba a seguir con la tabla de multiplicar del cuatro, pero de esa forma un tanto peculiar, y averiguar el motivo por el cual Alicia no llegaría nunca al veinte. Lo que os cuento en esta entrada del Cuaderno de Cultura Científica es hasta dónde me llevaron estas cuentas.
Distintas bases de numeración
Antes de seguir con esa curiosa tabla de multiplicar del cuatro, recordemos qué son las bases de numeración y cómo se representan los números naturales en las diferentes bases de numeración, de lo cual ya hemos hablado en algunas otras entradas del Cuaderno de Cultura Científica (como Las bases de numeración o cómo hacer trucos de magia binarios o Sobre cómo escribir el número pi en base cuatro). Aquellas personas que ya conozcan las bases de numeración pueden pasar directamente al siguiente apartado.
El sistema de numeración posicional moderno utilizado en casi todo el mundo es el decimal, es decir, que tiene base 10 (sobre este y otros sistemas de numeración puede consultarse el libro Los secretos de la multiplicación, de los babilonios a los ordenadores). Por lo tanto, consta de diez cifras básicas, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y todo número natural se puede representar con ellas al expresarlo en función de las potencias de 10. Por ejemplo, el número 273.054 tiene el valor de 2 veces la cantidad de 100.000 (centenas de millar), 7 veces la cantidad de 10.000 (decenas de millar), 3 veces la cantidad de 1.000 (unidades de millar), 0 veces la cantidad de 100 (centenas), 5 veces la cantidad de 10 (decenas) y 4 veces la unidad 1, que son las potencias de 10, a saber, 100.000 = 105, 10.000 = 104, 1.000 = 103, 100 = 102, 10 = 101 y 1 = 100.
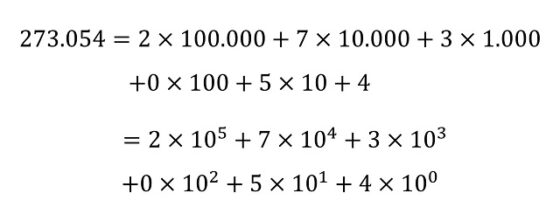
Aunque como se comentaba en la anterior entrada, El sistema de numeración en base Phi, existen otros sistemas de numeración posicionales en otras bases, como el sistema de numeración binario o en base 2, b = 2, que es el que utilizan nuestros ordenadores, los sistemas octal (base 8, b = 8) y hexadecimal (base 16, b = 16), que también son muy utilizados en informática, el sistema duodecimal o docenal (base 12, b = 12), que es por el que abogan como sistema cotidiano los miembros de las sociedades The Dozenal Society of America y The Dozenal Society of Great Britain, o el sistema sexagesimal (base sesenta, b = 60), que ya utilizaron los babilonios, pero en general para cualquier número natural b mayor o igual que 2, como b = 3 (sistema ternario), b = 4 (sistema cuaternario), b = 5 (quinario), etcétera.
En general, dada una base de numeración b –por ejemplo, como cualquiera de las que hemos comentado 2, 3, 4, 5, 8, 12, 16 o 60– la representación posicional de cualquier número natural en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i = 1, 2, 3, …, r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
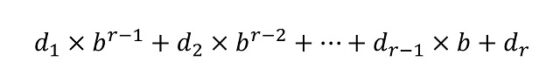
Por lo tanto, la representación del número está ligada a la base elegida. Por ejemplo, el número anterior 273.054 (escrito de forma natural, es decir, en base decimal), se representa de las siguientes formas en las distintas bases:
a) en la base binaria (b = 2), donde las cifras básicas son 0 y 1, como (1000010101010011110)2, ya que “273.054” = 218 + 213 + 211 + 29 + 27 + 24 + 23 + 22 + 21;
b) en la base ternaria (b = 3), para la cual las cifras básicas son 0, 1 y 2, como (111212120010)3, porque “273.054” = 1 x 311 + 1 x 310 + 1 x 39 + 2 x 38 + 1 x 37 + 2 x 36 + 1 x 35 + 2 x 34 + 1 x 31;
c) en la base cuaternaria (b = 4), siendo las cifras básicas 0, 1, 2 y 3, como (1002222132)4, porque “273.054” = 1 x 49 + 2 x 46 + 2 x 45 + 2 x 44 + 2 x 43 + 1 x 42 + 3 x 41 + 2 x 1;
d) en la base duodecimal (b = 12), donde las cifras básicas son denotadas por 0, 1, …, 9, A, B, como (112.026)12, porque “273.054” = 1 x 125 + 1 x 124 + 2 x 123 + 2 x 121 + 6;
e) en la base hexadecimal (b = 16), cuyas cifras básicas son denotadas por 0, 1, …, 9, A, B, C, D, E, F, como (42A9E)16, puesto que “273.054” = 4 x 164 + 2 x 163 + A x 162 + 9 x 16 + E;
donde estamos utilizando el subíndice de las representaciones (2, 3, 4, 12 y 16) para recordar que esa es una representación en esa base de numeración, y además, cuando la base b es mayor que 10 consideramos las letras del abecedario, en mayúsculas, como cifras básicas extra (A toma el valor de 10, B el valor de 11, C de 12, D de 13, etcétera).

Las multiplicaciones de Alicia
Una vez recordados los sistemas de numeración posicionales con diferentes bases b (siendo b un número natural mayor, o igual, que 2), podemos regresar a las multiplicaciones que comenta Alicia en el párrafo anterior. Empezaba así con la tabla del cuatro:
4 x 5 (= 20 = 1 x 18 + 2) = 1218 (base 18);
4 x 6 (= 24 = 1 x 21 + 3) = 1321 (base 21);
y la podemos continuar, como así hice yo nada más recibir el mensaje de Fátima con la esperanza de adivinar el motivo por el cual “de esta manera no llegaré nunca a veinte”, en la misma línea argumental como
4 x 7 (= 28 = 1 x 24 + 4) = 1424 (base 24);
4 x 8 (= 32 = 1 x 27 + 5) = 1527 (base 27);
4 x 9 (= 36 = 1 x 30 + 6) = 1630 (base 30);
4 x [10] (= 40 = 1 x 33 + 7) = 1733 (base 33);
4 x [11] (= 44 = 1 x 36 + 8) = 1836 (base 36);
4 x [12] (= 48 = 1 x 39 + 9) = 1939 (base 39);
y hasta aquí me habría quedado a las puertas del 20, que veremos a continuación si podemos alcanzarlo, o no. Pero antes un pequeño comentario. En la tabla de multiplicar del cuatro anterior ha llegado un momento en el que hemos denotado con corchetes las cifras básicas [10], [11], [12], para que quede claro qué multiplicación estamos realizando, pero que, si pensamos que son las cifras básicas del sistema de numeración de la base correspondiente (33, 36 y 39 en estos casos), deberíamos denotarlas con las letras A, B y C, que es la forma en la que hemos determinado que denotaremos las cifras básicas con valores por encima de 9. De esta forma las tres últimas líneas se podrían escribir como
4 x A (= 40 = 1 x 33 + 7) = 1733 (base 33);
4 x B (= 44 = 1 x 36 + 8) = 1836 (base 36);
4 x C (= 48 = 1 x 39 + 9) = 1939 (base 39).
Y ahora regresamos a esas puertas que nos separan de saber si podremos alcanzar el veinte (20) en la siguiente multiplicación, 4 por [13], o lo que es lo mismo, 4 x D. Veamos la multiplicación, que ahora, siguiendo la sucesión de bases (33, 36, 39), debería ser en base 42 (y ahí tenemos el mencionado número 42, que es “la respuesta definitiva a la vida, el universo y todo lo demás”):
4 x [13] (= 52 = 1 x 42 + 10) = 1[10]42 (base 42);
o, expresado con las cifras básicas A, B, C, etc,
4 x D (= 52 = 1 x 42 + 10) = 1A42 (base 42);
es decir, no obtenemos 20, sino 1A42 (o, lo que es lo mismo, 1[10]), en base 42. De esta manera el comentario de Lewis Carroll (bueno, del matemático británico Charles L. Dodgson (1832-1898), que firmaba con el seudónimo de Lewis Carroll), a través de Alicia, cobra todo el sentido, puesto que los resultados de la tabla del 4 en las respectivas bases son 12, 13, 14, 15, 16, 17, 18 y 19, seguido de 1A (en la base 42), pero no 20.
De hecho, el número 20 en la base 42 tendría el valor de 84 (en base decimal), puesto que
2042 = 2 x 42 + 0 = 84.

Un breve apunte histórico
El gran divulgador de las matemáticas estadounidense Martin Gardner (1914-2010), autor de la famosa columna de Juegos Matemáticos de la revista Scientific American, publicó en 1960 el libro Alicia anotada, que es una edición comentada de los dos cuentos de Lewis Carroll protagonizados por Alicia, Las aventuras de Alicia en el País de las Maravillas y Alicia a través del espejo. En esta publicación Gardner explica el párrafo de la tabla de multiplicar del cuatro en Alicia en el País de las Maravillas de la siguiente forma:
La explicación más sencilla de por qué Alicia nunca llegará a 20 es la siguiente: la tabla de multiplicar se detiene tradicionalmente en el 12, de manera que esta disparatada progresión (4 por 5, 12; 4 por 6, 13; 4 por 7; 14, etc) se termina en 4 por 12 (el máximo al que puede llegar), 19; justo uno menos de 20).
A mi entender, esta es una explicación un poco simple. Cuando empiezas a realizar las multiplicaciones (de bases cambiantes) sugeridas por Lewis Carroll, como me pasó a mí al recibir el mensaje de Fátima García Doval, te das cuenta de que llegas al clímax para la multiplicación 4 por [13], ya que no alcanzas el 20, no porque te hayas parado antes, sino porque el resultado es 1[10] en la correspondiente base (que es 42), es decir, es un argumento fundamentado en el sentido de las bases de numeración, que es la gracia del juego de Carroll.

De hecho, el biógrafo de Lewis Carroll, Alexander L. Taylor, autor de la biografía The White Knight, a study of C. L. Dodgson (Lewis Carroll) / El caballero blanco, un estudio sobre C. L. Dodgson (Lewis Carroll) publicada en 1952, explica en esta biografía la cuestión de la tabla de multiplicar del 4 de una forma muy similar a la que yo he explicado arriba, es decir, afirmando que 4 por [13] es 1[10] (en base 42), que es el motivo por el que no se alcanza el número 20. Aunque en la explicación de Taylor se habla de “escalas” en lugar de bases de numeración, lo que me hace sospechar que el biógrafo no entendía bien la explicación (sobre la que él alerta de su dificultad para los no matemáticos) que alguien le había proporcionado, tal vez el escritor británico Greville Macdonald (1856-1944), a quien Taylor menciona cuando introduce este “hermoso pequeño rompecabezas matemático” y a quien sus padres leyeron el manuscrito de Charles Dodgson antes de que fuese publicado.
¿De esta manera no llegaré nunca a veinte?
Si intentamos expresar el juego aritmético de forma general, observamos que Lewis Carroll (pseudónimo detrás del cual se esconde, como se ha comentado, el matemático Charles Dodgson), a través de Alicia, estaría realizando la tabla de multiplicar del 4, es decir, considerando las multiplicaciones 4 x n, pero tomadas en las bases 3n + 3 (para los números naturales n = 1, 2, 3, 4 etc), para cada n. Por ejemplo, si n = 5, la base es 18 o si n = 6, la base es 21.
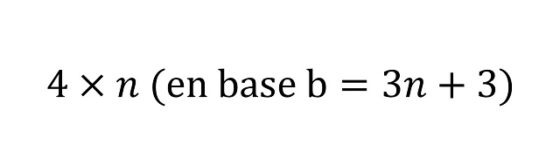
Más arriba hemos seguido las multiplicaciones a partir de n = 5, como nos indicaba Alicia, pero podríamos realizar también las anteriores, desde n = 1, como en cualquier tabla de multiplicar, obteniendo que
4 x 1 (= 4) = 46 (base 6);
4 x 2 (= 8) = 89 (base 9);
4 x 3 (= 12 = 1 x 12 + 0) = 1012 (base 12);
4 x 4 (= 16 = 1 x 15 + 1) = 1115 (base 15).
De esta manera, tendríamos la “tabla de multiplicar del 4” para esta multiplicación de bases cambiantes, para los primeros valores del multiplicador, n = 1, 2, 3, 4, 5, 6, 7, 8, 9, A = [10], B = [11], C = [12] y D = [13], pero podríamos continuar para más valores de n.
Por lo tanto, el juego planteado de forma general consistiría en saber si podrá existir algún número natural n para el cual el producto de 4 con el mismo, 4 x n, sea igual a 20 en base 3n + 3. Si tenemos en cuenta que veinte en base b (es decir, 20b) toma el valor de 2 x b y nos estamos preguntando si 4 x n puede ser 20b, entonces debe darse la igualdad
4 x n = (20b =) 2 x b = 2 x (3n +3),
esto es, 4n = 6n + 6, de donde 0 = 2n + 6, luego n = – 3, que es un número entero negativo, pero no un número natural (ya que no es positivo). En consecuencia, como ya sabíamos, no existe ningún número natural n para el cual obtengamos que 4 x n es igual a 20 en base 3n + 3, como preguntábamos. De nuevo, podemos afirmar que Alicia tenía toda la razón al afirmar que “de esta manera no llegaré nunca a veinte”.

Sin embargo, al resolver la ecuación asociada hemos obtenido una solución negativa, por lo que nos podemos plantear si existen las bases de numeración negativas y, en caso afirmativo, si podremos conseguir el veinte, pero a través de la multiplicación de 4 por un número negativo.
Los sistemas de numeración negativos
Los sistemas de numeración (posicionales) de diferentes bases b, siendo b un número natural (b = 2, 3, 4, etc), se remontan a la antigüedad. Como se explica en el libro Los secretos de la multiplicación, el primer sistema de numeración posicional fue utilizado por los eruditos de Babilonia, hacia el 2.000 a.n.e., y era un sistema de numeración sexagesimal, es decir, cuya base es b = 60 (sobre el mismo pueden leerse las entradas ¿Sueñan los babilonios con multiplicaciones eléctricas? o Sobre cómo escribir el número pi en base cuatro). Por otra parte, el primer sistema de numeración posicional decimal habría sido el sistema de numeración con varillas utilizado por los sabios chinos, japoneses y coreanos, desde el siglo v a.n.e. hasta el siglo XVI. Mientras que los Mayas utilizaron un sistema de numeración posicional en base 20, entre los siglos IV y IX.
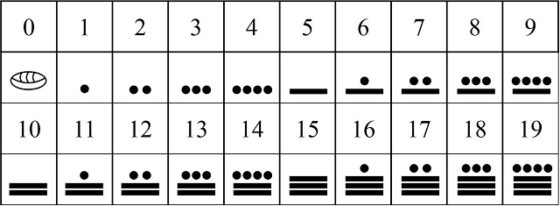
Como es bien conocido y hemos utilizado en esta entrada, para toda base b, siendo b un número natural mayor, o igual, que 2 (esto es, un número entero positivo, b = 2, 3, 4, 5, etc), se puede representar todo número natural de forma única. Lo que no es tan conocido es que si se utilizan las bases negativas (que efectivamente sí existen) se pueden representar de forma única todos los números enteros, es decir, también los negativos.
Como se explica en el volumen 2 del libro del experto en computación y matemático estadounidense Donald E. Knuth (1938), The Art of Computer Programming, las bases de numeración negativas son muy recientes. Los sistemas de numeración de base un entero negativo fueron considerados por primera vez por el profesor de matemáticas y lengua alemana italiano Vittorio Grünwald (1855-1943), en un artículo publicado en el Giornale di Matematiche di Battaglini en 1885, cuyo título era (en italiano) En torno a la aritmética de los sistemas numéricos de base negativa, centrándose en el sistema numérico de base decimal negativa para el estudio de sus analogías con la aritmética ordinaria (decimal). La siguiente aparición fue en 1936 de la mano del matemático estadounidense, nacido en Gran Bretaña, Aubrey J. Kempner (1880-1973), quien mencionaba brevemente las bases negativas en un pie de página de uno de sus artículos. Y pasaron otros veinte años para que las bases negativas fueran redescubiertas por los matemáticos polacos Zdzisław Pawlak y Andrzej Wakulicz, en dos artículos publicados en 1957 (Use of expansion with negative base in thearithmometer of digital computer) y 1959 (An electronic computer based on the “-2”system), y también por el estadounidense Louis B. Wadel, en una pequeña nota de 1957. En conclusión, los sistemas de numeración posicionales de bases negativas son muy, muy recientes, y prácticamente desconocidos.
Pero vayamos a la parte matemática de los sistemas de numeración con base un entero negativo. Sea b = – p, para p un número natural, entonces todo número entero se puede representar mediante una expresión d1d2…dr (donde los dígitos di –para i = 1, 2, 3, …, r– pertenecen a la familia de las p cifras básicas del sistema de numeración, que tienen valores entre 0 y p – 1) puesto que el número puede escribirse, de forma única, como
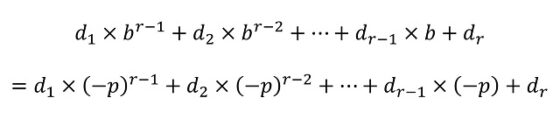
Veamos algunos ejemplos. Para empezar, consideremos la base b = – 10 (a este sistema de numeración se le llama “negadecimal”). Consideremos el número (decimal) 123, es decir, 1 x 102 + 2 x 10 + 3 = 100 + 20 + 3. Supongamos que fuese un número ABC en base –10, esto querría decir que
A x (–10)2 + B (–10) + C = 123,
y con un poco de álgebra básica tenemos que A = 2, B = 8 y C = 3. Por lo tanto, el número 123 puede escribirse en base –10 como
283(–10)
Si tomamos el número 123.456 (decimal) y lo pasamos a base negadecimal tenemos que es
1.937.556(–10)
ya que
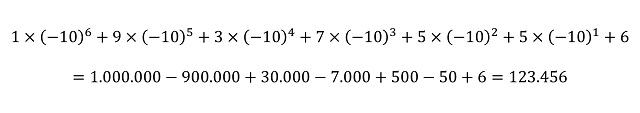
Pero como hemos comentado, esto también nos vale para los números enteros negativos. Vamos a utilizar como ejemplo el número – 123 (decimal), que se expresará en base negadecimal como
1.937(–10)
ya que 1 x (–10)3 + 9 x (–10)2 + 3 x (–10) + 7 = – 1.000 + 900 – 30 + 7 = – 123.
O, por incluir alguna otra base negativa, consideremos la base b = –2 (negabinaria), para la cual el número 123 (decimal) anterior se escribe como
110001111(–2)
como se desprende del hecho de que (–2)8 + (–2)7 + (–2)3 + (–2)2 + (–2) + 1 = 256 – 128 – 8 + 4 – 2 + 1 = 123. Mientras que – 123 (decimal) se escribe en base negabinaria como
10000101 (–2)
ya que (–2)7 + (–2)2 + 1 = – 128 + 4 + 1 = – 123.
Regreso al País de las Maravillas
Recordemos que hemos introducido los sistemas de numeración con bases negativas con el objetivo de ver si podemos conseguir “veinte” (20) a través de la multiplicación de 4 por un número negativo. Al plantear el problema de Alicia en el caso general, es decir, si 4 x n, puede ser igual a 20 en base 3n + 3, habíamos obtenido como solución n = –3, que en aquel momento no tenía sentido. Ahora, que sí lo tiene, veamos que es posible alcanzar el 20 al multiplicar 4 por – 3, en base 3 x (– 3) + 3 = – 6:
4 x (–3) (= – 12 = 2 x (–6)) = 20(–6) (base – 6).
Por supuesto que esto no cambia para nada el argumento de Lewis Carroll y la belleza de su juego numérico, pero me ha permitido divertirme con estas ideas, que es el objetivo de todo juego, incluidos los rompecabezas matemáticos.
Por otra parte, en la época en la que Lewis Carroll, es decir, Charles Dodgson, escribió Las Aventuras de Alicia en el País de las Maravillas (1865) no se conocían las bases de numeración negativas, que tardarían 20 años (después de la publicación de la novela) en aparecer, aunque pasaron desapercibidas mucho tiempo, como se ha comentado más arriba, podríamos decir que más allá de la mitad del siglo xx. De hecho, realmente empezaron a conocerse un poco más cuando Martin Gardner escribió sobre ellas en su columna de Juegos Matemáticos de la revista Scientific American, en 1972.

Bibliografía
1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.
2.-Página web Alice-in-wonderland.net: Alice-in-wonderland.net [https://www.alice-in-wonderland.net/]
3.- Alexander L. Taylor, The White Knight, a study of C. L. Dodgson (Lewis Carroll), Oliver and Boyd, 1952.
4.- Lewis Carroll, Alicia anotada: 150 aniversario, Edición de Martin Gardner, actualización de Mark Burstein, Akal, 2017.
5.- Donald E. Knuth, The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, Addison-Wesley, 1998.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
