La ingeniería de las flautas (2/5)

La flauta travesera: una pieza de ingeniería de precisión que, a otra escala, no desmerecería por su apariencia en una refinería de petróleo. Pero también un concepto musical y artístico que nos acompaña desde el mismo amanecer de la cultura. ¿Cómo funciona? Comencemos por el principio.
¿Hace una cerveza?
No es mi intención fastidiar a mis lectores abstemios: una botella de refresco pequeña también os servirá. A los demás, os propongo para este experimento que sigáis estos pasos:
- Seleccionad vuestro proveedor favorito de zumo de cebada. No, ese no; y ese otro tampoco; algunos tenemos principios, ¿sabéis?
- Bebed, bebed y sed felices. Pero no os paséis de un tercio de litro; no deseo que el fomento de la embriaguez acabe formando parte de mi currículum. Además, el experimento es más fácil con un quinto o un tercio que con algo más grande.
- Tomad la botella vacía. Ponedla verticalmente frente a vosotros, de forma que vuestros labios rocen su boca —y disculpad la involuntaria resonancia erótica.
- Con los labios solo ligeramente abiertos, pero relajados, exhalad vuestro aliento de forma continua y firme de modo que el aire forme un chorro perpendicular a la abertura de la boca de la botella.
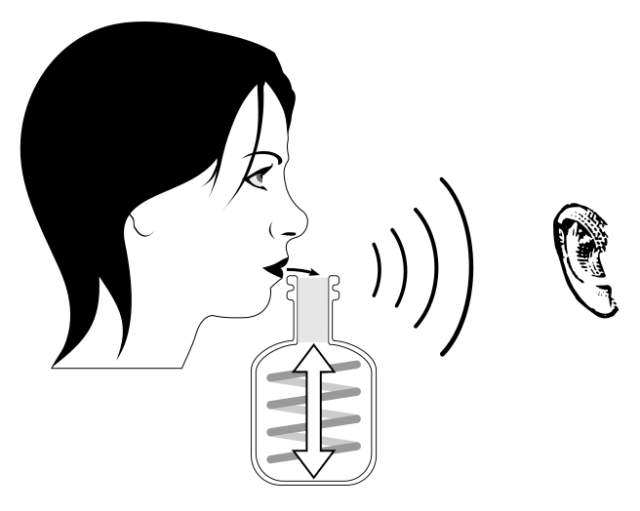
Si habéis seguido mis instrucciones estaréis oyendo un sonido penetrante. Quien quiera que esté con vosotros en este momento querrá mandaros a las inmediaciones del río Marsyas, en la antigua Frigia, a soplarle a la botellita. Ahora intentad tensar y cerrar más los labios. Intuitivamente, el aire así expulsado sale más rápido; Bernoulli tendría algo que decir sobre esto. Comprobad cómo, tras quizá algunos intentos, el sonido se hace más agudo y penetrante de lo que podríais haber imaginado. Observad con maravilla cómo se multiplican las ansias de vuestros acompañantes por enviaros al Marsyas, quizá con la botella transformada por obra y gracia de la inquina y el odio humanos en instrumento de tortura. ¿Qué está pasando?
Sin llegar al punto de postular la famosa vaca esférica —pero casi— vamos a simplificar un poco. Supongamos que nuestra botella es tan solo un tubo: un cilindro perfecto, abierto por un extremo y cerrado por el otro. Ahora vamos a fijarnos en qué hace el aire dentro de ese cilindro. ¿No hace nada? Disculpad, se me olvidaba. Soplemos como antes lo hacíamos en la botella.
El esqueleto de la teoría
El aire es un medio elástico. Para entender esto, basta con considerar qué ocurre si apretamos un poco un globo hinchado ¡sin pasarse, no queremos reventarlo! Pongamos el globo sobre una mesa y presionemos con la mano desde arriba. El globo se deforma de un modo bastante intuitivo, y recupera su forma original cuando dejamos de aplicar la fuerza. Consideremos ahora un globo dentro de un recipiente cilíndrico abierto por arriba. Con esto impediremos que la forma del globo cambie, pero al aplicar la misma fuerza que antes el globo también se deformará. Estamos comprimiendo el aire; cuando dejemos de apretar, el globo volverá a expandirse elásticamente.
Hemos usado un globo solo para poder «tocar» la deformación elástica del aire; sin globo el efecto es más sutil (y, desde luego, invisible). Si soplamos en la boca del tubo cerrado como hicimos antes en la botella estamos aplicando una fuerza compresiva sobre el aire allí contenido. Parte del chorro de aire que sale de nuestra boca entrará en el tubo, fijando un valor de flujo de aire máximo para ese punto. Éste irá disminuyendo conforme avanzamos por su eje hasta hacerse nulo en el fondo. Con la presión del aire ocurrirá lo contrario: la abertura del cilindro está a la misma presión que la atmósfera. El exceso de aire provocado por el soplo hará que la presión aumente hasta llegar a un máximo en el fondo del tubo —no habrá una gran diferencia, pero será suficiente para lo que va a suceder.
El aumento de la presión en el fondo del tubo provoca que el aire contenido responda de forma elástica. Mientras no desaparezca la fuente de excitación en el sistema —nuestro soplo— el aire proyectado entrará y saldrá del tubo periódicamente. Solo tenemos que ajustar la velocidad del aire que sale de nuestra boca para encontrar la resonancia del sistema y la energía de nuestro soplo se habrá transformado en una nota clara: la fundamental de nuestro instrumento.
Ya es bastante increíble que una excitación continua —un soplo— pueda inducir una respuesta de naturaleza ondulatoria —un sonido— en un tubo, pero la cosa no se queda ahí. Como hemos visto antes con la botella, tensando los labios podemos obtener notas más agudas. (Ejercicio para el lector: ¿cuántas notas por encima de la fundamental puedes obtener de tu botella? ¿Cuánto tiempo hace falta para que se presente la policía en casa, alertada por algún vecino desesperado?)
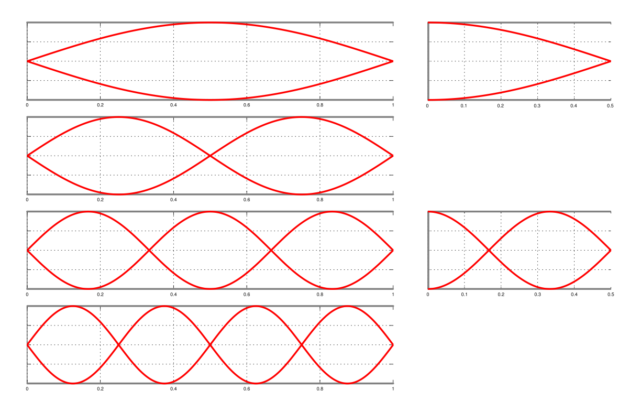
Lo que está ocurriendo es que al introducir aire en el tubo a mayor velocidad podremos encontrar resonancias a frecuencias más altas que cumplen lo que matemáticos, físicos e ingenieros llamamos condiciones de contorno y que antes os he colado sin darles su nombre técnico. Fijando el máximo de flujo de aire en el borde abierto del tubo y el mínimo (cero) en el fondo —y al revés para la presión: la de la atmósfera en la boca, y el máximo en el fondo, nos cabe un cuarto de onda dentro del tubo, y por tanto la longitud de onda de la nota fundamental es igual a la longitud del tubo multiplicada por cuatro. Pero, apretando un poco más, caben tres cuartos de onda (para una longitud de onda emitida igual a la del tubo multiplicada por cuatro tercios). ¿Más madera? Podríamos hacer encajar una onda entera y un cuarto, con una longitud de onda igual a la del tubo por cuatro quintos. Y así sucesivamente.
La longitud de onda se hace más pequeña, y por tanto la frecuencia —ni más ni menos que el número de veces por segundo que la onda oscila— crece, en relación inversa según una fórmula sencilla que mostró Newton:
velocidad del sonido = frecuencia × longitud de onda
La velocidad del sonido en el aire es un valor que puede determinarse experimentalmente y que depende de la temperatura. En aire seco y a 20 °C es de 343,2 m/s; un poco menos si hace más frío, un poco más si hace más calor. Esto significa que podríamos predecir a qué frecuencia sonará un tubo tan solo midiéndolo, como habría hecho un antiguo constructor de flautas. ¿No habéis tenido suficiente con la botella? En el siguiente artículo de esta serie os propondré un experimento.
Referencias
[1] S. A. Wicks, «Flutes or piccolos could harm your hearing», http://www.larrykrantz.com/flutesor.htm, consultado el 16/07/2016.
[2] S. Münzel et al., «The Geißenklösterle Flute – Discovery, Experiments, Reconstruction», Studien zur Musikarchäologie III; Archäologie früher Klangerzeugung und Tonordnung; Musikarchäologie in der Ägäis und Anatolien, Orient-Archäologie, 2002, tomo 10, ed. Verlag Marie Leidorf GmbH, Rahden/Westfalen; pp. 107-118.
[3] D. Buisson, «Les flûtes paléolithiques d’Isturitz (Pyrénées-Atlantiques)», Bulletin de la Société Préhistorique Française, 1990, tomo 87, nos. 10-12, pp. 420-433.
[4] T. Higham et al., «Τesting models for the beginnings of the Aurignacian and the advent of figurative art and music: The radiocarbon chronology of Geißenklösterle», Journal of Human Evolution, 2002, pp. 1-13.
[5] Pseudo-Plutarco, «De fluviis», cap. X, s. III-IV EC, ed. W. W. Goodwin, Little, Brown & Co., Cambridge, Massachussetts, 1874.
[6] I. Newton, «Principia Mathematica Philosophiae Naturalis», libro II, sección VIII, pág. 363 y ss., 1687, trad. y ed. I. Bruce., 2012.
[7] gStrings Tuner, https://play.google.com/store/apps/details?id=org.cohortor.gstrings, cohortor.org, consultado el 16/07/2016.
[8] J. Wolfe, «Flute acoustics, an introduction», http://newt.phys.unsw.edu.au/jw/fluteacoustics.html, University of New South Wales, Australia, consultado el 16/07/2016.
[9] A. Botros, The Virtual Flute, http://flute.fingerings.info/, consultado el 16/07/2016.
Sobre el autor: Iván Rivera es ingeniero de telecomunicaciones y aprendiz perpetuo de flautista.

Lo Mejor de la Semana 222 (24-30 de julio) | Hablando de Ciencia
[…] semana Iván Rivera nos deleita con la ingeniería de las flautas: 1 y sus orígenes frigios, 2 y el experimento de la botella de cerveza o de refresco para los abstemios, 3 y más experimentos […]
QS – La física que no se ve: Aprendiendo en vacaciones. #1
[…] Fuente de la imagen del soplo del botellín: https://culturacientifica.com/2016/07/26/la-ingenieria-las-flautas-25/ […]
M Carmen Fuentes Gimeno
Muchas gracias por estos artículos tan interesantes y de manera tan amena contados.
Slaudos
Carmen Fuentes