Uno de los libros de divulgación de las matemáticas que más me influyó en mi juventud fue El hombre anumérico, El analfabetismo matemático y sus consecuencias (Tusquets, 1990), del matemático y divulgador estadounidense John Allen Paulos.

El libro está lleno de interesantes ejemplos sobre la importancia de entender la probabilidad y cómo en ocasiones esta nos demuestra que nuestra intuición se equivoca. Muchos de estos ejemplos los he rescatado para mis artículos, conferencias, talleres y libros, como la conocida paradoja del cumpleaños, aunque seguramente mi primera lectura de la misma fue de la mano del gran maestro de la divulgación matemática, el estadounidense Martin Gardner (1914-2010), en su libro ¡Ajá! Paradojas. Paradojas que hacen pensar (Labor, 1983); el bonito ejemplo de la probabilidad de que llueva el fin de semana, que utilicé para el video de la sección Una de mates del programa de La 2 de televisión española Órbita Laika que podéis ver en la entrada Una de mates: la probabilidad de que llueva el fin de semana; el ejemplo de los falsos positivos en las pruebas médicas para detectar una enfermedad, con el que inicié la entrada Falsos positivos o la importancia de comprender la información; o el juicio en California “a la mujer rubia peinada con una cola de caballo y al hombre negro con barba y bigote”, ejemplo del mal uso de la probabilidad en los juicios (otros ejemplos de este estilo aparecen en la entrada La probabilidad en el banquillo de los acusados).

En el capítulo Probabilidad y coincidencia de El hombre anumérico también se incluían ejemplos sobre el lanzamiento de una moneda al aire. La probabilidad de que salga cara, o cruz, cuando lanzamos una moneda al aire –que en cualquiera de los dos casos es del 50%–, es el primer ejemplo que siempre se utiliza para explicar el concepto matemático de probabilidad, del que además derivan situaciones más complejas e incluso anti-intuitivas.

El lanzamiento de una sola moneda al aire, apostando a que salga cara o cruz, es el juego de azar más sencillo que existe, que además es un juego justo, ya que las dos personas que juegan tienen una probabilidad del 50% de ganar, siempre que no hagamos trampas.

La probabilidad es la matemática del azar, nos proporciona una medida de cuánto de probable es que un evento ocurra. Por lo tanto, si jugamos a un juego de azar contra otra persona y la probabilidad de ganar no es igual para ambas, está claro que a la larga ganará el jugador que tenga una probabilidad mayor del 50%. En conclusión, el conocimiento de la probabilidad de ganar en un juego de azar nos proporciona la información necesaria para saber si debemos de jugar o no, e incluso, cómo debemos de jugar para ganar. Un ejemplo clásico que ilustra esta idea es el problema de Monty Hall, donde hay una estrategia que nos asegura ganar con una probabilidad de 2/3 contra 1/3, como explicamos en el video de la sección Una de mates del programa Órbita Laika titulado precisamente El problema de Monty Hall.

En esta entrada del Cuaderno de Cultura Científica vamos a mostrar un juego, justo en apariencia, pero realmente desigual, el juego de Penney, que podríamos llamar también el juego de la secuencia de tres tiradas de una moneda.

Este juego fue introducido por el matemático Walter Penney en la revista Journal of Recreational Mathematics, en 1969; Martin Gardner lo explicó en su columna de juegos matemáticos de la revista Scientific American y apareció posteriormente en su libro Viajes en el tiempo y otras perplejidades matemáticas (1988); aunque yo creo haberlo leído por primera vez, y si lo leí antes no lo recuerdo, en el libro Matemáticas y juegos de azar de John Haigh (2003).

Imaginemos que lanzamos una moneda al aire tres veces seguidas. Las posibles secuencias de tres lanzamientos son

CCC, CCX, CXC, XCC, CXX, XCX, XXC, XXX,

si denotamos por C el lanzamiento que es una cara y X el que es una cruz. Cada una de esas secuencias tiene una probabilidad de salir de 1/8 (una de cada ocho secuencias de tres tiradas), es decir, un 12,5%.

Podemos plantear el siguiente juego de azar para jugar con otra persona. Le pedimos que elija una secuencia de tres tiradas posible, de las ocho que existen, y nosotros elegiremos otra. Por ejemplo, puede haber elegido CCX y nosotros XCC. Y tiramos tres veces la moneda, si sale alguna de las dos opciones elegidas, gana el jugador que ha elegido esa secuencia, en caso de no salir ninguna se vuelve a tirar la moneda otras tres veces seguidas. Así hasta que salga una de las dos secuencias elegidas y gane uno de los dos jugadores.

Veamos el ejemplo de dos partidas, en la primera gana mi contrincante al salir CCX antes que XCC, mientras que la segunda es al revés.

CCC XXC XXC XCX CCX

CXC XCX CXX XCC

Los dos jugadores tienen, en cada ronda de tres lanzamientos, la misma probabilidad de que salga su jugada, un 12,5%, por lo que nos encontramos ante un juego justo.

El matemático Walter Penny planteó una pequeña variación de este juego. Consiste en lo siguiente, lanzar la moneda de forma consecutiva y no en grupos de tres lanzamientos como antes. De esta manera, se considera ganador el jugador cuya jugada de tres lanzamientos consecutivos salga primero dentro de la serie continua de lanzamientos. Veamos un ejemplo. Supongamos la primera partida de las dos anteriores, pero como la tomamos como una secuencia de lanzamientos consecutivos, sería

C C C X X C X X C X C X C C X.

Entonces, el primer grupo de tres lanzamientos consecutivos es CCC como antes, pero al lanzar la moneda otra vez y obtener X, se genera el siguiente grupo de tres lanzamientos consecutivos CCX, así van obteniéndose CXX, XXC, XCX, CXX, XXC, etcétera, como se muestra en la siguiente imagen.

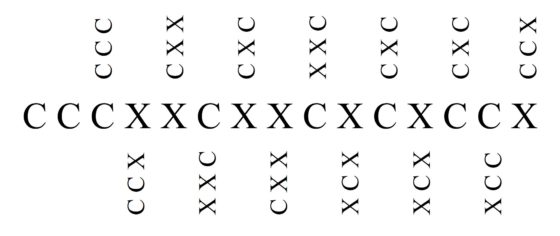
De manera que al lanzar la moneda quince veces seguidas, que en la primera ocasión eran cinco sucesiones de tres lanzamientos consecutivos, de esta otra forma se generan trece sucesiones de tres lanzamientos consecutivos. Más aún, en esta partida, siguiendo las reglas del juego de Penny, ganaría mi contrincante al salir CCX después de los cuatro primeros lanzamientos (CCCX).

El hecho de que se realicen los lanzamientos seguidos genera más resultados concatenados y nos ahorra tiradas en el juego. Pero no ha cambiado solo eso. Contrariamente a lo que pueda parecer, ahora ya no es un juego justo.

Veamos un ejemplo para ilustrarlo. Imaginemos que la persona contra la que jugamos elige CCC, entonces si nosotros elegimos XCC, tendremos una probabilidad de ganar de 7/8 (87,5%) contra una probabilidad de 1/8 (12,5%) que tendrá la persona contra la que jugamos. Esto se debe a que, si sale CCC en los tres primeros lanzamientos, lo cual tiene una probabilidad de ocurrir de 1/8, luego sucederá una de cada ocho veces, ganará nuestra adversaria, mientras que en las otras siete veces, de cada ocho, ganaremos nosotros con la jugada XCC. ¿Por qué? Si no ha salido CCC en los tres primeros lanzamientos, después ocurre lo siguiente. Imaginemos que la primera secuencia de tres lanzamientos CCC no se produce en los tres primeros lanzamientos del juego, entonces necesariamente en el lanzamiento anterior a esos tres habrá salido una X, siendo la serie de tres lanzamientos anterior XCC, con lo cual ganaríamos nosotros. Es decir, siempre que aparezca CCC –que no sea en los tres primeros lanzamientos– habrá salido justo antes XCC.

Lo mismo ocurre para las demás opciones, siempre que elijamos nuestra jugada convenientemente tras la elección de jugada por parte de la persona contra la que estamos jugando al juego de Penney. Dada la elección de nuestra oponente, nosotros tomaremos los dos primeros elementos de su jugada –por ejemplo, si esta ha sido CCX tomaremos CC– y los pondremos en las dos últimas posiciones de nuestra jugada, evitando además que nuestra jugada sea capicúa –luego nuestra jugada en el ejemplo sería XCC–.

En la siguiente tabla mostramos las diferentes opciones de jugada de nuestra oponente y nuestras elecciones, siguiendo la norma anterior, así como las probabilidades de ganar que tenemos, que van desde 2/3 (66,6%) hasta 7/8 (87,5%), siempre por encima del 50%. Es decir, ganaremos a la larga si jugáramos a este juego, siempre que elijamos jugada en segundo lugar, aunque parezca que es un juego justo.

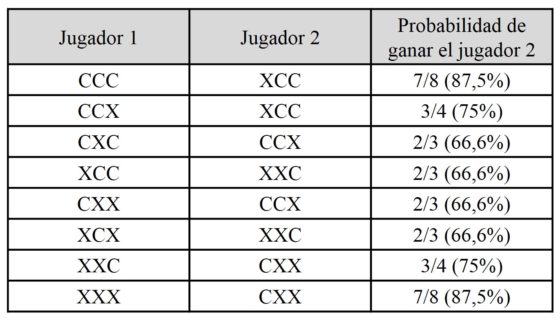
Este es un juego que tiene la apariencia de ser un juego justo, en el que los dos jugadores tienen una probabilidad de ganar del 50%, pero no es así, como se ha visto. Por este motivo, si alguien que conozca el juego nos plantease jugar, podríamos caer en la trampa –siempre que nosotros no lo conozcamos– de jugar contra esa persona.

Ilustremos la información de la anterior tabla en el siguiente diagrama.

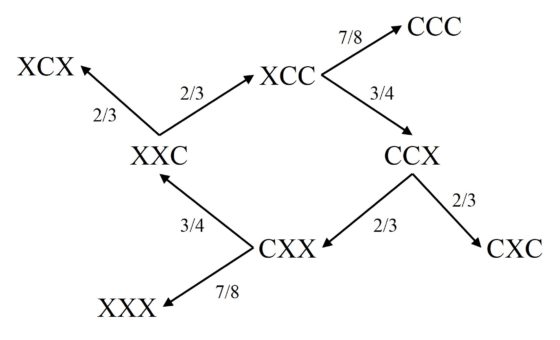
Por lo tanto, el juego de Penney es lo que se llama un juego no transitivo. La jugada XCC gana a la jugada CCX, la cual gana a la jugada CXX, la cual gana a la jugada XXC, mientras que esta finalmente gana a la inicial XCC, cerrando el ciclo. Sin embargo, en un juego transitivo, si XCC gana a CCX, que gana a CXX, que gana a XXC, entonces la primera XCC debería ganar a la última XXC, pero no es así.

El juego no transitivo más popular es piedra, papel, tijera. Ya sabéis … piedra gana a tijera, tijera gana a papel y papel gana a piedra.

Si tuviésemos en cuenta secuencias de solo dos tiradas la cuestión no es tan favorable. Si el primer jugador elige la jugada CC, el segundo jugador elegiría la jugada XC y ganaría con una probabilidad de 3/4, como ocurría en el caso de secuencias de tres jugadas (recordemos que cada una de las cuatro opciones CC, CX, XC, XX tiene una probabilidad de salir de 1/4). Lo mismo ocurre con la jugada XX, a la que gana la jugada CX tres de cada cuatro veces. Sin embargo, si el primer jugador elige XC, podemos elegir XX o CX, pero solo tendremos una probabilidad de ganar de 1/2, el 50%. Lo mismo ocurriría con la jugada CX.

Para secuencias de cuatro lanzamientos, o más, ocurre como en el juego de Penney descrito, se puede obtener una estrategia ganadora para el segundo jugador.

Bibliografía

1.- John Allen Paulos, El hombre anumérico, El analfabetismo matemático y sus consecuencias, Metatemas 20, Tusquets editores, 1990.

2.- Martin Gardner, ¡Ajá! Paradojas. Paradojas que hacen pensar, Labor, 1983.

3.- Raúl Ibáñez, La probabilidad a juicio, en El secreto de los números, Universidad de Alicante, 2016.

4.- Martin Gardner, Viajes en el tiempo y otras perplejidades matemáticas, Labor, 1988.

5.- John Haigh, Matemáticas y juegos de azar, Jugar con la probabilidad, Metatemas 78, Tusquets editores, 2003.

6.- Matt Parker, Pi-fias Matemáticas, Crítica, 2020.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica