Homenaje alfabético a Georg Cantor
El matemático Georg Cantor (1845-1918) nació un 3 de marzo. Este retrato alfabético es un modesto homenaje a un genial matemático que ha marcado tanto mi investigación como mi docencia a lo largo de mi carrera.
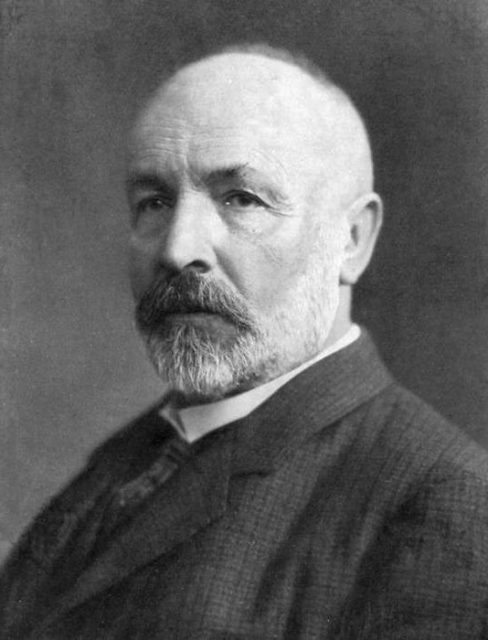
APEIROFOBIA
Esta palabra procede del término griego «Ápeiron» que fue utilizado por Anaximandro para referirse al «arjé», al elemento primordial de la realidad. Suele traducirse por «ilimitado», «infinito» o «indeterminado».
En la hermosa novela Villa des hommes (2007) de Denis Guedj, el protagonista, Hans Singer (un álter ego de Georg Cantor), se refiere a esta «fobia al infinito» de esta manera: «Cuando comencé con mis investigaciones, la mayor parte de mis colegas, así como los de las generaciones que me habían precedido, sufrían una enfermedad particular: apeirofobia. […] Apeirofobia, señor Matthias, o fobia al infinito».
BLASFEMIA
Cantor fue acusado de blasfemia por algunos colegas que no entendían sus novedosas teorías respecto a la teoría de conjuntos y otros aspectos de las matemáticas. Muchos de ellos, sin duda, padecían «apeirofobia».
CONJUNTO TERNARIO DE CANTOR
Entre 1879 y 1884, Cantor escribió una serie de cinco artículos que contienen, entre otros, el primer tratamiento sistemático de la topología de la recta real. En el quinto artículo de esta serie, introdujo lo que se conoce como el conjunto ternario de Cantor, un conjunto infinito, perfecto y totalmente disconexo. Es un modelo topológico para cierto tipo de espacios en el sentido que indica este teorema: «Todo espacio métrico no vacío, totalmente disconexo, perfecto y compacto es homeomorfo al conjunto ternario de Cantor».
DEPRESIÓN
Cantor sufrió episodios recurrentes de depresión desde 1884 hasta el final de su vida. Algunos de sus biógrafos los atribuyen a un posible trastorno bipolar que se manifestaba, en particular, en momentos en los que sus colegas matemáticos rechazaban sus teorías. En varias ocasiones ingresó en hospitales psiquiátricos, donde no dejó de pensar y escribir sus teorías matemáticas.
ESENCIA (DE LAS MATEMÁTICAS)
Una de las más famosas citas de Georg Cantor es: «La esencia de las matemáticas radica en su libertad».
FILOSOFÍA
Georg Cantor discutió los aspectos filosóficos de sus teorías matemáticas sobre el infinito con diferentes científicos.
GENIO
El matemático David Hilbert describió el trabajo de Georg Cantor como «el mejor producto del genio matemático y uno de los logros supremos de la actividad humana puramente intelectual».
HIPÓTESIS DEL CONTINUO
La hipótesis del continuo es un enunciado relativo a la cardinalidad del conjunto de los números reales; fue formulado como una conjetura por Cantor en 1878. Afirma que no existen conjuntos infinitos cuyo cardinal esté estrictamente comprendido entre el del conjunto de los números naturales y el del conjunto de los números reales.
Fue una conjetura tan notoria que acabó siendo uno de los 23 problemas de Hilbert propuestos en 1900. La hipótesis del continuo es indecidible, es decir, partiendo de los axiomas de la teoría de conjuntos no puede probarse ni refutarse. Kurt Gödel demostró su consistencia (no puede refutarse) en 1940 y Paul Cohen probó su indecibilidad (no puede demostrarse) en 1963.
INFINITO
Antes de las teorías de Cantor, solo se consideraban conjuntos finitos y «el infinito», pensado como un asunto de discusión filosófica más que matemática. Al demostrar que hay una infinidad de posibles «tamaños» para conjuntos infinitos, Cantor mostró que la teoría de conjuntos debía revisarse.
JOURDAIN
Cantor mantuvo correspondencia con el lógico Philip Jourdain sobre la teoría de conjuntos en la que ambos trabajaban.
KRONECKER
Leopold Kronecker fue uno de sus profesores más admirados por Cantor en la Universidad de Berlín. Su radical oposición a las novedosas teorías matemáticas de Cantor provocó una profunda enemistad entre ambos. Kronecker llegó a calificar a su pupilo de «charlatán científico, renegado y corruptor de la juventud».
LO VEO PERO NO LO CREO
Cantor mantuvo correspondencia durante varios años con Richard Dedekind, compartiendo sus ideas y solicitando la opinión de su colega matemático. En 1877, Cantor escribió a Dedekind para compartir su demostración de la existencia de una biyección entre el intervalo [0 ,1] y el espacio n-dimensional. Sorprendido de su propio descubrimiento, Cantor escribió: «Lo veo, pero no lo creo».
MITTAG-LEFFLER
Cantor también mantuvo correspondencia con el matemático sueco Gösta Mittag-Leffler. Fue a partir de 1882 y duró tres años, se interrumpió tras un desencuentro entre ambos científicos. Mittag-Leffler pidió a Cantor que retirara una propuesta de artículo para Acta Mathematica (fundada por el matemático sueco)por considerarla demasiado adelantada a su tiempo, y Cantor decidió dejar de publicar en esa revista.
NÚMEROS
Cantor demostró que los números racionales y los algebraicos son numerables, es decir, pueden ponerse en correspondencia biunívoca con los números naturales. También probó que los números reales no son numerables, usando el conocido como argumento diagonal de Cantor.

ORDINALES Y CARDINALES
Cantor desarrolló una teoría de conjuntos infinitos, llamados cardinales (y su aritmética) y ordinales (y su aritmética), que ampliaba la aritmética de los números naturales.
PARAÍSO
David Hilbert defendió con vehemencia las teorías de Cantor ante las críticas de otros colegas. En 1926, Hilbert escribía: «Nadie debería poder expulsarnos del paraíso que ha creado Cantor para nosotros».
QUIMERA
Muchos de sus colegas pensaban que las teorías de Cantor eran quimeras, delirios, fantasías.
RELIGIÓN
Cantor estuvo preocupado por preservar la ortodoxia de la relación entre Dios y las matemáticas. En 1905, escribió una obra religiosa tras regresar a casa después de una temporada en un hospital psiquiátrico.
SAN PETERSBURGO
Georg Cantor nació en San Petersburgo y se crio allí hasta los once años. La familia se mudó a Alemania en 1856, al enfermar el padre.
TEORÍA DE CONJUNTOS
El comienzo de la teoría de conjuntos como rama de las matemáticas tiene como origen un artículo de Cantor de 1874 (Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen). En este artículo se encuentra la primera prueba rigurosa de la existencia de más de un tipo de infinito.
UNIVERSIDAD DE HALLE
En 1867, tras defender su tesis (tutelado por Eduard Kummer y Karl Weierstrass) en la Universidad de Berlín, Cantor pasó a ocupar un puesto en la Universidad de Halle, donde desarrolló toda su carrera.
VALLY GUTTMANN
En 1874, Cantor se casó con Vally Guttmann, una amiga de su hermana. El matrimonio tuvo seis hijos.
WILLIAM SHAKESPEARE
Cantor poseía una curiosa creencia literaria; estaba convencido de que Francis Bacon era en realidad el autor de las obras teatrales atribuidas a William Shakespeare. En 1884, durante una de sus estancias en un sanatorio psiquiátrico, comenzó un intenso estudio de la literatura isabelina para intentar probar la teoría baconiana. Publicó dos panfletos sobre este tema en 1896 y 1897.
XIX
El siglo XIX vivió grandes cambios en las matemáticas gracias, en parte, a las propuestas revolucionarias de Georg Cantor.
Y…
… llegamos al final de este homenaje, con la Z, y los conjuntos como protagonistas.
ZERMELO-FRAENKEL
Los axiomas de Zermelo-Fraenkel son un sistema axiomático concebido para formular la teoría de conjuntos. Como ya hemos comentado, la hipótesis del continuo es indecidible en este sistema.
«Me imagino un conjunto como un abismo».
Georg Cantor
Referencias:
-
O’Connor, John J.; Robertson, Edmund F., Georg Cantor, MacTutor History of Mathematics archive, University of St Andrews
-
Joseph Warren Dauben, Georg Cantor: his Mathematics and Phylosophy of the infinite, Princeton University Press, 1990
-
Georg Cantor, Wikipedia
Para saber más:
Apeirofobia
Una mirada topológica al conjunto de Cantor
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
Homenaje alfabético a Georg Cantor &mdas…
[…] Un retrato alfabético es una lista de palabras ordenadas alfabéticamente que se convierte en el retrato de Georg Cantor […]
Un retrato alfabético de la topología
[…] introdujo lo que se conoce como el conjunto ternario de Cantor, un conjunto infinito, perfecto y totalmente disconexo. Es un modelo topológico para cierto tipo de espacios en el sentido que indica este teorema: […]