No es la primera vez que aludo a Georg Cantor (1845-1918) en este Cuaderno de Cultura Científica. Su figura y su obra matemática me fascinan. He tenido la suerte de tener muy presentes sus matemáticas en mi investigación y mi docencia. Probablemente Cantor fue una de esas pocas personas que es capaz de “pensar” las cosas de otra manera. Esa mirada distinta, genial y osada, provocó grandes cambios en la manera de entender y abordar las matemáticas.

Uno de los más bellos ejemplos que nos ha proporcionado es el conocido como conjunto de Cantor.

En realidad –al menos como registro publicado conocido– fue el matemático Henry J. Stephen Smith quien introdujo este tipo de conjunto en 1874, en el artículo On the Integration of Discontinuous Functions(Proc. London Math. Soc. 1 (6): 140-153): tras una exposición sobre la integración de funciones discontinuas, presentaba un método para construir conjuntos densos en ninguna parte:

Sea m un número entero mayor que 2. Se divide el intervalo [0,1] en m partes iguales y se suprime el último segmento de cualquier división posterior. Se dividen cada uno de los m-1 segmentos restantes en m partes iguales y se eliminan los últimos segmentos de cualquier división posterior. Si esta operación se continúa ad infinitum, se obtiene una cantidad infinita de puntos de división P en el intervalo [0,1]. Estos puntos forman un conjunto denso en ninguna parte…

Aunque no se dice explícitamente en el enunciado, los intervalos eliminados son abiertos, con lo que el conjunto resultante P es cerrado. En el momento actual, el conjunto descrito por Smith se llamaría conjunto de Cantor generalizado.

Entre 1879 y 1884, Cantor escribió una serie de cinco artículos que contienen, entre otros, el primer tratamiento sistemático de la topología de la recta real. En el quinto artículo de esta serie, Cantor discute las particiones de un conjunto en dos componentes que llama reducible y perfecta, y define lo que es un conjunto

perfecto. Muestra que un conjunto perfecto no es necesariamente denso, y en un pie de página introduce su famoso conjunto ternario, el conjunto de los puntos que pueden expresarse de la forma (*):

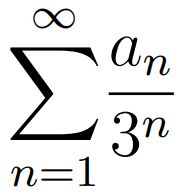
donde a_n=0 ó 2.

Cantor prueba que este conjunto es infinito, perfecto y que no es denso en ningún intervalo (es totalmente disconexo, es decir, sus componentes conexas son sus puntos).

Puede darse una construcción geométrica alternativa (pueden verse los detalles en [3]) y fácil de entender. Se toma el intervalo [0,1], se divide en tres partes iguales de longitud 1/3 y se elimina el intervalo abierto central (1/3,2/3). Con los dos intervalos cerrados restantes se repite la misma operación: cada uno de los intervalos [0,1/3] y [2/3,1] se divide en tres intervalos de la misma amplitud (en este caso 1/9) y se eliminan los intervalos centrales (1/9,2/9) y (7/9,8/9). Quedan entonces cuatro intervalos cerrados: [0,1/9], [2/9,1/3], [2/3,7/9] y [8/9,1], con los que se repetirá el mismo proceso, y así de manera indefinida. El conjunto resultante es el conjunto ternario de Cantor. Es fácil probar que los puntos del ternario de Cantor son precisamente los elementos del intervalo [0,1] que se pueden expresar de la forma (*) con a_n=0,2.

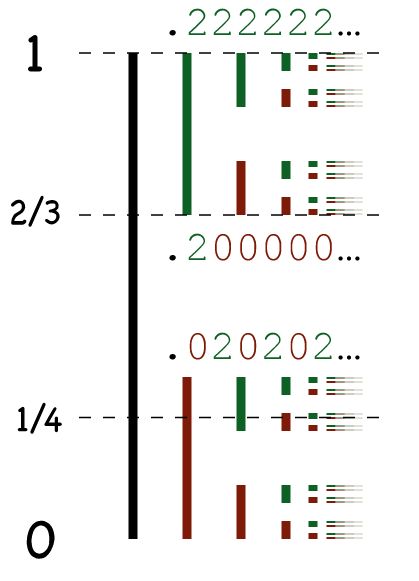
De hecho, los elementos del primer intervalo abierto eliminado en la construcción, (1/3,2/3), son los que tienen en la expresión (*) el coeficiente a₁=1. Los puntos de los intervalos abiertos eliminados en el segundo paso de la construcción –(1/9,2/9) y (7/9,8/9)– tienen el coeficiente a₂=1 en la suma (*). De hecho, los puntos de (1/9,2/9) tienen como primeros coeficientes en (*) a₁=0 y a₂=1; y los de (7/9,8/9) a₁=2 y a₂=1. En el paso n de esta iteración, los intervalos abiertos eliminados corresponden a los puntos con a_n=1 en la expresión (*). Por eso, al final del proceso de construcción, los puntos que quedan, los del ternario de Cantor, son los que se escriben según la expresión (*) con coeficientes a_n=0 ó 2.

La suma de las longitudes de los intervalos abiertos eliminados en este proceso es 1, dicho de otra manera, el conjunto de Cantor es de medida 0. Es uno de los primeros ejemplos de conjunto de medida nula que se dan en un curso de Análisis. Pero para mí, como topóloga, la propiedad más importante del conjunto de Cantor es que es un modelo topológico de cierto tipo de espacios métricos, los expresados en el siguiente teorema (ver [4]):

Todo espacio métrico totalmente disconexo, perfecto y compacto es homeomorfo al conjunto ternario de Cantor.

Un hermoso ejemplo de conjunto que cumple las propiedades del anterior teorema es el collar de Antoine, del que hablamos en este blog: es un conjunto topológicamente equivalente al conjunto de Cantor, que parte de una construcción sobre un sólido de dimensión tres.

Se puede realizar la misma construcción que la del ternario de Cantor eliminando de [0,1] un intervalo abierto (por ejemplo, el central) de longitud 1/4. De los dos intervalos cerrados restantes se elimina el intervalo abierto central de longitud 1/16, y así sucesivamente. Al final del proceso, la suma de las longitudes de los intervalos abiertos eliminados es 1/2. Es decir, el conjunto restante –que es homeomorfo al conjunto de Cantor, según el teorema anterior– mide 1/2. Es una manera de comprobar que la medida no es una propiedad topológica.

El conjunto ternario de Cantor tiene otras muchas propiedades sorprendentes… pero esa es otra historia.

Referencias:

[1] La biografía Georg Cantor: his Mathematics and Phylosophy of the infinite(1990), escrita por Joseph Warren Dauben, es probablemente una de las mejores maneras de aprender sobre la vida del matemático.

[2] Recomiendo también la bellísima biografía novelada Villa del hommes (2007) de Denis Guedj, en la que se reconoce a Georg Cantor en la figura del viejo matemático Hans Singer, recluido en un manicomio.

[3] Marta Macho Stadler, Curiosidades sobre el conjunto de Cantor, Un Paseo por la Geometría 1999/2000 (2001) 97-116

[4] Stephen Willard, General Topology, Addison Wesley, 1970

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad