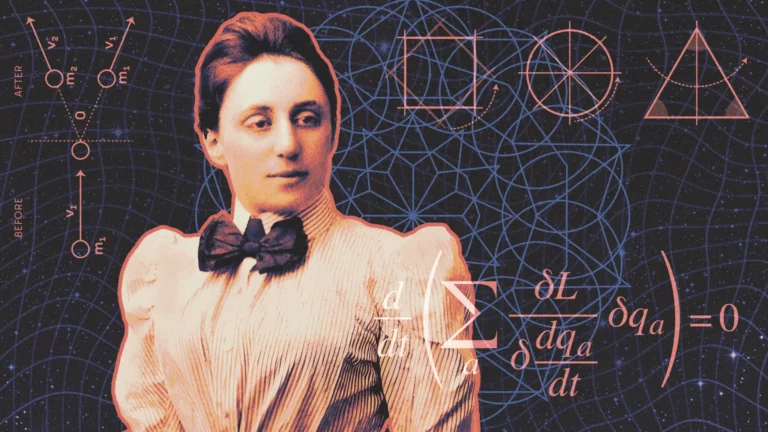Emmy Noether demostró que las leyes físicas fundamentales son solo una consecuencia de simetrías simples. Un siglo después, sus ideas siguen dando forma a la física.

Un artículo de Shalma Wegsman. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

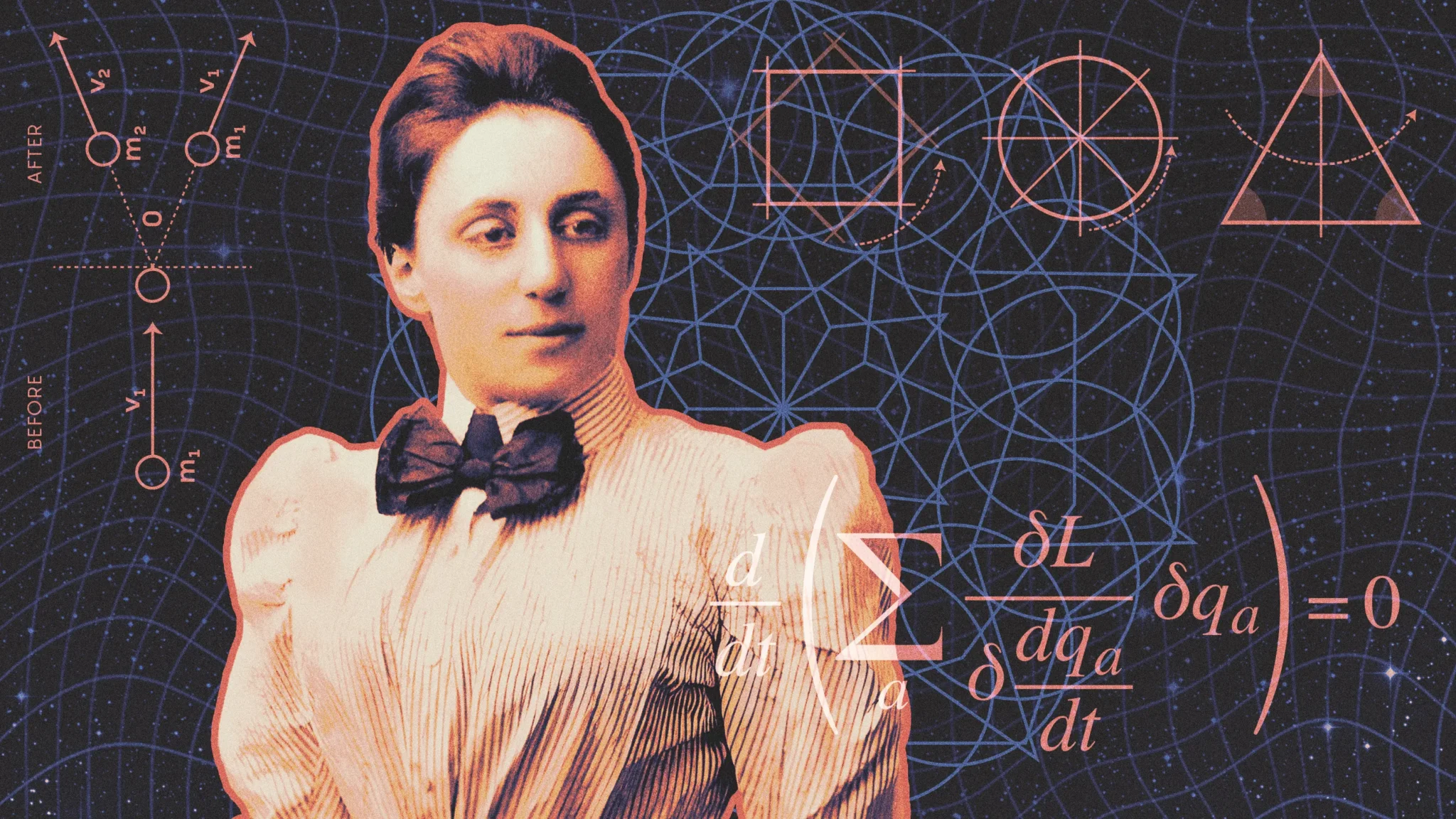
En el otoño de 1915, los cimientos de la física empezaron a resquebrajarse. La nueva teoría de la gravedad de Einstein parecía implicar que debería ser posible crear y destruir energía, un resultado que amenazaba con trastocar dos siglos de pensamiento en la física.

La teoría de Einstein, llamada relatividad general, transformó radicalmente el significado del espacio y el tiempo. En lugar de ser telones de fondo fijos de los acontecimientos del universo, el espacio y el tiempo eran ahora personajes por derecho propio, capaces de curvarse, expandirse y contraerse en presencia de materia y energía.

Un problema con este espacio-tiempo cambiante es que, a medida que se estira y se encoge, la densidad de la energía en su interior cambia. Como consecuencia, la ley clásica de conservación de la energía que describía toda la física no encajaba en este marco. David Hilbert, uno de los matemáticos más destacados de la época, identificó rápidamente este problema y se propuso, junto con su colega Felix Klein, tratar de resolver este aparente fallo de la relatividad. Cuando no pudieron resolverlo, Hilbert le pasó el problema a su asistente, Emmy Noether, de 33 años.

Noether era asistente solo de nombre. Ya era una matemática formidable cuando, a principios de 1915, Hilbert y Klein la invitaron a unirse a ellos en la Universidad de Gotinga. Pero otros miembros de la facultad se opusieron a contratar a una mujer, y a Noether se le impidió unirse a la facultad. A pesar de todo, pasaría los siguientes tres años presionando la falla que separa la física de las matemáticas, lo que finalmente desencadenó un terremoto que sacudiría los cimientos de la física fundamental.

En 1918, Noether publicó los resultados de sus investigaciones en dos teoremas fundamentales. Uno explicaba las leyes de conservación en pequeñas regiones del espacio, una proeza matemática que más tarde resultaría importante para comprender las simetrías de la teoría cuántica de campos. El otro, ahora conocido simplemente como el teorema de Noether, dice que detrás de cada ley de conservación se esconde una simetría más profunda.

En términos matemáticos, una simetría es algo que le puedes hacer a un sistema sin que cambie. Consideremos el acto de rotación. Si comenzamos con un triángulo equilátero, veremos que podemos rotarlo en múltiplos de 120 grados sin que cambia su apariencia. Si comenzamos con un círculo, podemos rotarlo cualquier ángulo. Estas acciones sin consecuencias revelan las simetrías subyacentes de estas formas.

Pero las simetrías van más allá de la forma. Imagina que haces un experimento, luego te mueves 10 metros hacia la izquierda y lo vuelves a hacer. Los resultados del experimento no cambian, porque las leyes de la física no cambian de un lugar a otro. Esto se llama simetría de traslación.

Ahora espera unos días y repite el experimento. Los resultados no cambian, porque las leyes de la física no cambian con el paso del tiempo. Esto se llama simetría de traslación temporal.

Noether comenzó con simetrías como estas y exploró sus consecuencias matemáticas. Trabajó con la física establecida utilizando una descripción matemática común de un sistema físico, llamada lagrangiano.

En este punto, la intuición de Noether trascendió los símbolos en la página. Sobre el papel, las simetrías no parecen tener ningún impacto en la física del sistema, ya que no afectan al lagrangiano. Pero Noether se dio cuenta de que las simetrías deben ser importantes desde el punto de vista matemático, ya que limitan como puede comportarse un sistema. Trató de determinar cuál debería ser esta restricción y, de las matemáticas del lagrangiano, surgió una cantidad que no puede cambiar. Esa cantidad corresponde a la propiedad física que se conserva. El impacto de la simetría había estado oculto bajo las ecuaciones todo el tiempo, fuera de la vista.

En el caso de la simetría de traslación, el momento total del sistema nunca debería cambiar. En el caso de la simetría de traslación temporal, la energía total de un sistema se conserva. Noether descubrió que las leyes de conservación no son axiomas fundamentales del universo, sino que surgen de simetrías más profundas.

Las consecuencias conceptuales son difíciles de exagerar. Los físicos de principios del siglo XX se sorprendieron al darse cuenta de que un sistema que rompe la simetría de traslación temporal puede romper con ella la conservación de la energía. Ahora sabemos que nuestro propio universo hace esto. El cosmos se está expandiendo a un ritmo acelerado, estirando la luz sobrante del universo primitivo. El proceso reduce la energía de la luz a medida que pasa el tiempo.

“Antes del teorema de Noether, el principio de conservación de la energía estaba envuelto en misterio”, escribió el físico y matemático Feza Gürsey en 1983. “… La formulación matemática simple y profunda de Noether hizo mucho por desmitificar la física”.

El teorema de Noether también ha influido en el mundo cuántico. En la década de 1970, desempeñó un papel importante en la construcción del Modelo Estándar de la física de partículas. Las simetrías de los campos cuánticos dictan leyes que restringen el comportamiento de las partículas fundamentales. Por ejemplo, una simetría en el campo electromagnético obliga a las partículas a conservar su carga.

El poder del teorema de Noether ha inspirado a los físicos a buscar la simetría para descubrir nueva física. Más de un siglo después, las ideas de Noether siguen influyendo en la forma de pensar de los físicos.

“Hay mucho que todavía nos queda por aprender si reflexionamos sobre el teorema de Noether”, afirma el físico matemático John Baez. “Tiene capas y capas de profundidad”.

El artículo original, How Noether’s Theorem Revolutionized Physics, se publicó el 7 de febrero de 2025 en Quanta Magazine.

Traducido por César Tomé López