Los tensores se utilizan en matemáticas y ciencias para revelar verdades geométricas ocultas. ¿Qué son?

Un artículo de Joseph Howlett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

Tras publicar su teoría especial de la relatividad en 1905, Albert Einstein dedicó la década siguiente a desarrollar una teoría de la gravedad. Sin embargo, durante años, se enfrentó a un problema constante.

Quería demostrar que la gravedad es en realidad una deformación de la geometría del espacio-tiempo causada por la presencia de materia. Pero también sabía que el tiempo y la distancia son, contrariamente a la intuición, relativos: cambian según el marco de referencia. Moverse rápidamente acorta las distancias y ralentiza el tiempo. ¿Cómo, entonces, describir la gravedad objetivamente, independientemente de si uno está quieto o en movimiento?

Einstein encontró la solución en una nueva teoría geométrica publicada unos años antes por los matemáticos italianos Gregorio Ricci-Curbastro y Tullio Levi-Civita. En esta teoría se sentaron las bases matemáticas de lo que posteriormente se denominaría «tensor».

Desde entonces, los tensores han desempeñado un papel fundamental no solo en la teoría general de la relatividad de Einstein, sino también en el aprendizaje automático, la mecánica cuántica e incluso la biología. «Los tensores son el mecanismo de empaquetado más eficiente que tenemos para organizar nuestras ecuaciones», explica Dionysios Anninos, físico teórico del King’s College de Londres. «Son el lenguaje natural de los objetos geométricos».

También son difíciles de definir. Si hablas con un informático, podría decirte que un tensor es una matriz de números que almacena datos importantes. Un solo número es un tensor de “rango 0”. Una lista de números, llamada vector, es un tensor de rango 1. Una cuadrícula de números, o matriz, es un tensor de rango 2. Y así sucesivamente.

Pero si hablas con un físico o una matemática, esta definición les parecerá insuficiente. Para ellos, aunque los tensores pueden representarse mediante esas disposiciones de números, tienen un significado geométrico más profundo.

Para comprender la noción geométrica de tensor comienza con los vectores. Imagina un vector como una flecha que flota en el espacio: tiene una longitud y una dirección. (Esta flecha no necesita estar anclada a un punto específico: si la mueves en el espacio sigue siendo el mismo vector). Un vector podría representar la velocidad de una partícula, por ejemplo, donde la longitud indica su rapidez y la dirección, su rumbo.

Esta información se empaqueta en una lista de números. Por ejemplo, un vector en un espacio bidimensional se define mediante un par de números. El primero indica cuántas unidades se extiende la flecha hacia la derecha o hacia la izquierda, y el segundo indica cuánto se extiende hacia arriba o hacia abajo.

Pero estos números dependen de cómo hayas definido tu sistema de coordenadas. Supongamos que cambias tu sistema de coordenadas:

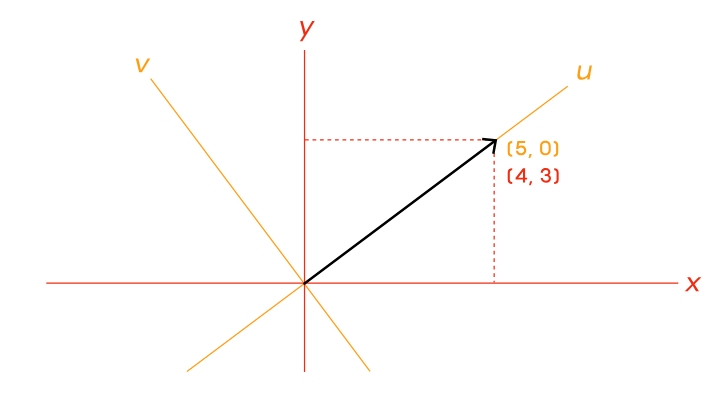
Ahora expresas el vector en términos de su extensión en cada dirección del nuevo sistema de coordenadas. Esto te da un par de números diferente. Pero el vector en sí no ha cambiado: su longitud y orientación permanecen iguales, independientemente del sistema de coordenadas en el que te encuentres. Además, si sabes cómo cambiar de un sistema de coordenadas a otro, también sabrás automáticamente cómo debería cambiar tu lista de números.

Los tensores generalizan estas ideas. Un vector es un tensor de rango 1; los tensores de rango superior contienen información geométrica más compleja.

Por ejemplo, imagina que tienes un bloque de acero y quieres describir todas las fuerzas que se pueden ejercer sobre él. Un tensor de rango 2, escrito como una matriz, puede lograrlo. Cada cara del bloque percibe fuerzas en tres direcciones diferentes. (Por ejemplo, la cara derecha del bloque puede percibir fuerzas de arriba a abajo, de izquierda a derecha y de adelante hacia atrás).

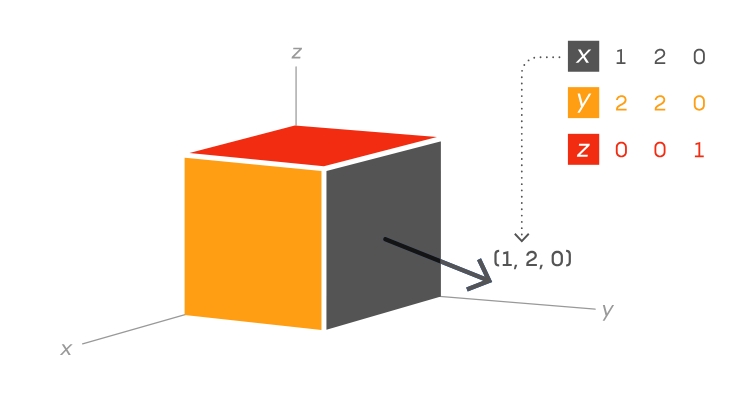
El tensor que encapsula todas estas fuerzas puede, por lo tanto, representarse mediante una matriz de nueve números: un número por cada dirección para cada una de las tres caras. (Las caras opuestas, en este ejemplo, se consideran redundantes).

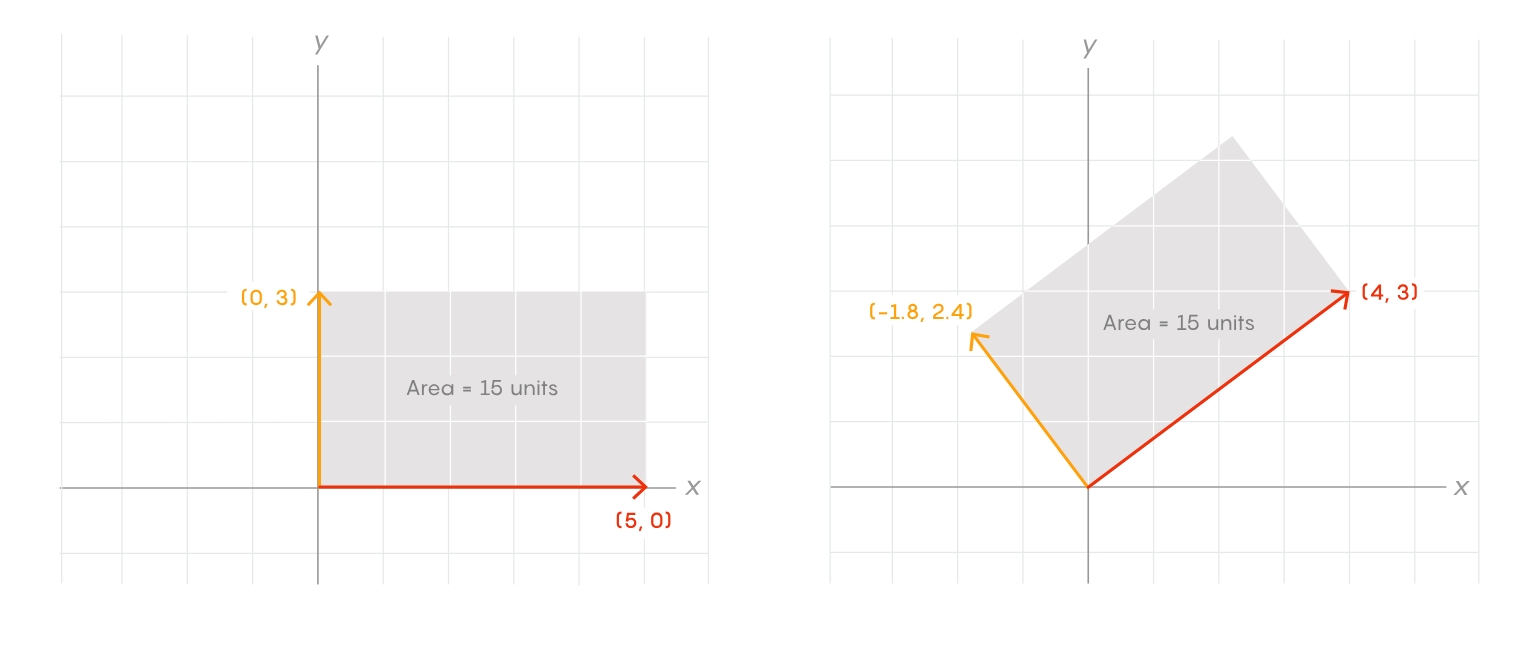
Los matemáticos suelen concebir los tensores como funciones que toman uno o más vectores como entrada y producen otro vector, o un número, como salida. Esta salida no depende del sistema de coordenadas elegido. (Esta restricción es lo que distingue a los tensores de las funciones en general). Un tensor podría, por ejemplo, tomar dos vectores que forman las aristas de un rectángulo y obtener como salida el área del rectángulo. Si se gira el rectángulo, su longitud a lo largo del eje x y su altura a lo largo del eje y cambiarán. Pero su área no.

En la teoría de la relatividad de Einstein, la distancia y el tiempo —que antes se consideraban absolutos— resultan ser variables para distintos observadores. Pero, al igual que la longitud y la altura pueden combinarse para calcular el área, la distancia y el tiempo pueden combinarse para definir otras propiedades fijas o invariantes. Los tensores permitieron a Einstein manipular eficientemente estos invariantes y describir la relación entre la masa y el espacio-tiempo. Pudo escribir una única ecuación que describiera cómo la materia curva el espacio-tiempo, condensando lo que de otro modo habrían sido 16 ecuaciones independientes e interconectadas.

Desde la publicación de esta ecuación en 1915, los tensores se han vuelto omnipresentes. Los físicos los utilizan para caracterizar el movimiento de los electrones alrededor de los núcleos atómicos o para describir el estado de un sistema cuántico entrelazado. Los informáticos los utilizan para almacenar los parámetros de los modelos de aprendizaje automático. Los biólogos los usan para rastrear rasgos a lo largo de un linaje. Y los matemáticos los multiplican para construir tensores aún más complejos y luego estudian los nuevos espacios en los que habitan. Los tensores pueden ayudar a los matemáticos a explorar simetrías complejas, analizar propiedades de formas especiales llamadas variedades e investigar las relaciones entre diferentes funciones, entre otras cosas.

Einstein una vez le rogó a un amigo que le ayudara a comprender los tensores, temiendo volverse loco. Pero los comprendió, y desde entonces han sido clave para que los científicos puedan describir nuestro mundo.

El artículo original, The Geometric Tool That Solved Einstein’s Relativity Problem, se publicó el 12 de agosto de 2024 en Quanta Magazine.

Traducido por César Tomé López