Tetris, embaldosados y demostraciones
En una de las recientes entradas de la sección Matemoción del Cuaderno de Cultura Científica, “Embaldosando con L-triominós (Un ejemplo de demostración por inducción)”, estuvimos hablando de poliominós, de problemas de embaldosados con algunos tipos particulares de estas figuras geométricas, en concreto, los L-triominós, de una demostración por inducción y del diseño de un juego comercial relacionado con estas cuestiones. En la entrada de hoy vamos a centrarnos en otro tipo de poliominós diferentes, los tetraminós, y en un par de problemas de ingenio de teselaciones con estas figuras geométricas.

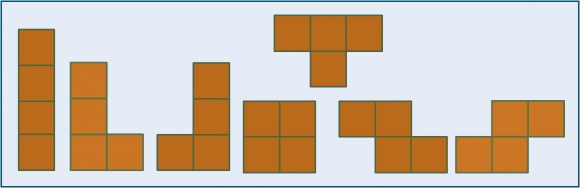
Recordemos que un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro. Si unimos cuatro cuadrados se tiene precisamente un tetraminó (o tetrominó). Existen cinco tipos de tetraminós distintos (que se denotan por la similitud con la forma de alguna de las letras del abecedario, como I, L, O, T, Z), aunque también podemos considerar que son siete si nos referimos a los “tetraminós planos”, es decir, que solamente podemos moverlos en el plano (rotarlos o trasladarlos), ya que si se pueden mover en el espacio, los dos tetraminós “con forma de L” (el L y el J) son el mismo, así como los dos “con forma de Z” (el Z y el S).
Aunque pueda sorprender a priori, un videojuego basado en los tetraminós se convirtió a finales de los años 80 y en los años 90 en un juego muy popular. Es el conocido Tetris. Este juego fue diseñado y programado por Alekséi Pázhitnov, mientras trabajaba para el Centro de Computación Dorodnitsyn de la Academia de Ciencias de la Unión Soviética en Moscú. Para ello se inspiró en el juego de los pentominós, a cuya versión comercial había estado jugando previamente. El creador de los poliominós, Solomon W. Golomb, al introducirlos en los años 50, se había centrado en los pentominós y en las posibilidades matemáticas y recreativas de estos. El “juego de los penominós” consistía en formar, con los 12 pentominós que hay, rectángulos de tamaño 6 x 10, 5 x 12, 4 x 15 o 2 x 30 (puesto que el área que cubren los 12 pentominós es de 60 “unidades cuadradas”, 12 x 5 = 60), e incluso rectángulos más pequeños con solo algunas de las doce piezas.

Como todas nuestras lectoras y lectores sabrán, el juego del Tetris consiste en lo siguiente. En la parte superior de la pantalla (véase la siguiente imagen) van apareciendo, uno a uno y sin ningún orden establecido, “tetraminós planos” y van descendiendo poco a poco. El jugador, con los mandos del videojuego, podrá dejar la pieza en la posición que está o rotarla un ángulo de 90°, 180° o 270°, así como moverla a derecha o izquierda, con el fin de encajarla lo mejor posible en la parte inferior de la pantalla, donde estarán las piezas que ya han ido saliendo, e intentando dejar la menor cantidad de huecos posible. Cuando una línea horizontal se completa, esa línea desaparece y todas las piezas que están por encima descienden una posición. El juego se termina si las piezas se han amontonado hasta llegar a la parte superior de la pantalla, no permitiendo salir más fichas.

El Tetris fue lanzado en junio de 1984 (en EEUU en 1986). Su nombre deriva del prefijo “tetra” (en referencia a su origen geométrico, los “tetraminós”) y de “tenis”, el deporte favorito de Alekséi. Pero fue su programación para IBM PC por parte del joven Vadim Gerasimov, que trabajaba también en la Academia, lo que provocó que el juego empezara a ser más popular. Y así fue evolucionando hasta llegar a Nintendo y a su nueva consola portátil, Game Boy. Hoy en día el videojuego tiene versión para todo tipo de dispositivos (consolas de videojuegos, PCs, teléfonos móviles, PDAs, etc). En los años 80 este videojuego se vendió para una amplia gama de ordenadores domésticos y se convirtió en uno de los juegos más populares de todos los tiempos tras salir la versión para la consola Game Boy. Según la wikipedia, en 2007, el juego del Tetris ocupó el segundo lugar en la lista de los “100 mejores videojuegos de todos los tiempos” para IGN Entertainment, se [.]. hhan vendido más de 70 millones de copias del mismo, y solo desde 2005 más de 100 millones de copias para móviles.

Pero vayamos al tema central de esta entrada del Cuaderno de Cultura Científica, los problemas de embaldosados con tetraminós y su resolución. El primer juego de ingenio que traemos aquí es el puzzle de los tetraminós. Como ya hemos comentado anteriormente, existen 5 tetraminós distintos (I, L, O, T, Z), y como cada uno está formado por 4 cuadrados, entonces el área total de los cinco tetraminós es de 5 x 4 = 20 “unidades cuadradas”, al igual que el área de una superficie rectangular de tamaño 5 x 4. Por lo tanto, el problema es el siguiente:
El puzzle de los tetraminós: formar un rectángulo de tamaño 5 x 4 (como el que aparece en la imagen) con los cinco tetraminós distintos (I, L, O, T, Z).
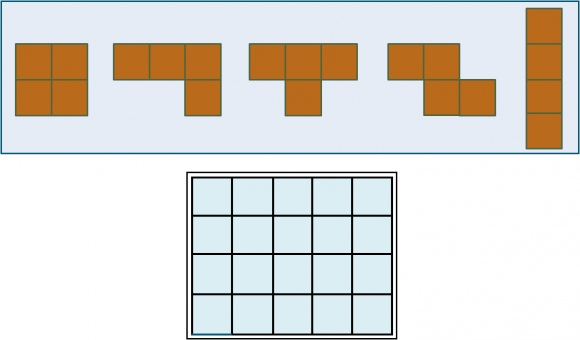
Lo mejor de los juegos o problemas de ingenio es ponerse a jugar, a intentar resolverlos, por lo tanto recomiendo a quien esté leyendo este artículo que interrumpa momentáneamente su lectura y que prepare con algún material que tenga a mano (papel, cartulina, madera, azulejos cuadrados,… ¡todo vale!) los cinco tetraminós. Y una vez construidas las piezas geométricas, disfrute intentando formar un rectángulo de tamaño 5 x 4 con las mismas. Mientras os ponéis a construir estas figuras geométricas para jugar al puzzle de los tetraminós, os dejo con las imágenes de algunos anuncios publicitarios en los que aparece una imagen relacionada con el Tetris.
Algunos anuncios publicitarios que utilizan la imagen del Tetris. Otros anuncios pueden encontrarse en los artículos de divulgamat “Los anuncios Tetris” primera parte y segunda parte
¿Os habéis animado a intentar solucionar el problema? ¿Habéis conseguido construir el rectángulo 5 x 4 con los cinco poliominós que están formados con cuatro cuadrados? ¿Aún no habéis conseguido resolver el puzzle? ¿Quizás es que no es posible montar un rectángulo de tamaño 5 x 4 con los cinco tetraminós?
Cuando nos enfrentamos a un juego de ingenio como el puzzle de los tetraminós, hay dos opciones. Puede que tenga solución, lo que suele ser lo más habitual, en cuyo caso se tratará de obtener una solución del mismo (o varias, si es que existe más de una), quizás con la sencilla técnica del “ensayo-error” o diseñando una estrategia más elaborada que nos permita llegar a obtenerla. Pero también podría ocurrir que el puzzle no tenga solución, y la cuestión será entonces demostrar de alguna forma la imposibilidad de resolverlo. No basta con que tengamos la sospecha, necesitamos demostrarlo.
Pero volvamos al puzzle de los tetraminós… si llevamos un tiempo intentando resolverlo, pero no lo hemos conseguido, ¿será, como comentábamos arriba, que no tiene solución? Si no la tiene, ¿cómo podríamos demostrarlo? Existe una ingeniosa demostración de este hecho basada en la idea del tablero de ajedrez, similar a la solución al problema de la teselación con dominós del tablero de ajedrez sin dos esquinas que vimos en la entrada “Embaldosando con L-triominós (Un ejemplo de demostración por inducción)”.

En primer lugar, se pinta el tablero rectangular de tamaño 5 x 4 sobre el que colocar los cinco tetraminós como si fuera un tablero de ajedrez, es decir, se pintan los cuadrados alternando dos colores, por ejemplo, blanco y negro (como se muestra en la imagen). A continuación, se trata de ver cuántos cuadrados blancos y negros cubre cada una de las piezas del puzzle, los tetraminós. Los que reciben el nombre de I, O, L y Z claramente van a cubrir siempre dos cuadrados blancos y dos negros. Mientras que el T-tetraminó cubrirá un cuadrado negro y tres blancos, o al revés, uno blanco y tres negros, dependiendo de donde lo coloquemos. En consecuencia, los cinco tetraminós colocados en el tablero no pueden cubrir la misma cantidad de cuadrados blancos y negros, a pesar de que en un rectángulo 5 x 4, como el de la imagen, hay tantos cuadrados blancos como negros. Por lo tanto, no es posible construir con dichas piezas un rectángulo. El puzzle no tiene solución.
Otra ingeniosa demostración, aunque algo más elaborada, de un problema similar de teselaciones, pero en esta ocasión con copias de una única pieza, el L-tetraminó, lo leí no hace mucho tiempo en el excelente libro Famous Puzzles of Great Mathematicians (AMS, 2009) de Miodrag S. Petkovic. Era un problema de Fuchs y Tabachnikov, que decía así.
Problema del embaldosado con L-tetraminós: ¿Es posible embaldosar un cuadrado de tamaño 10 x 10 (luego formado por 100 pequeñas unidades cuadradas) con L-tetraminós (que tienen 4 unidades cuadradas cada uno)?

Este es otro problema, al igual que el anterior, que no tiene solución. La cuestión es que una vez que empezamos a sospechar que es uno de esos puzzles imposibles, ¿cómo demostrar que no se puede teselar el cuadrado 10 x 10 con L-tetraminós? La demostración de Fuchs y Tabachnikov es realmente ingeniosa.
En este caso, se escriben 1s y 5s en las celdillas cuadradas del tablero 10 x 10, como se muestra en la siguiente imagen. Las celdas de la primera fila tienen 1s, las de la segunda fila 5s, las de la tercera 1s, las de la cuarta 5s, y así hasta abajo.
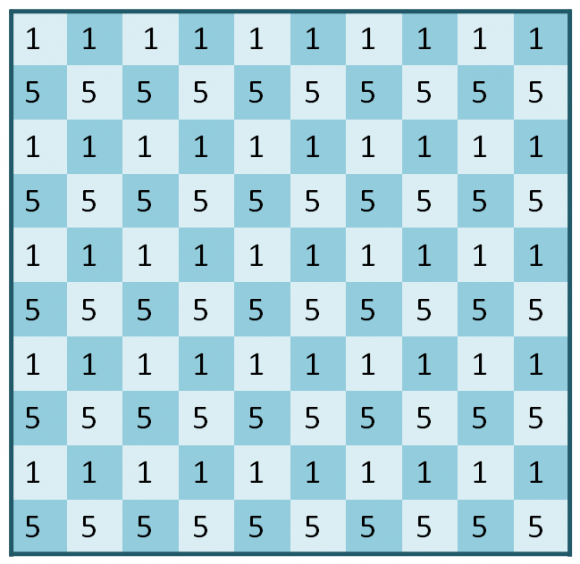
Ahora, hay que observar que cada pieza con forma de L-tetraminó cubrirá tres 1s y un 5, o tres 5s y un 1, dependiendo de donde la coloquemos, luego la suma de los números de las celdas que cubre un L-tetraminó es 1+1+1+5 = 8 o 5+5+5+1=16, es decir, en ambos casos múltiplo de 8. En consecuencia, si cubrimos el tablero 10 x 10 con piezas de L-tetraminós, la suma total de los números de las celdas cubiertas, que será todo el tablero 10 x 10, tendrá que ser múltiplo de 8. Sin embargo, si sumamos todos los números que aparecen en la imagen del tablero 10 x 10, el resultado es 5 x 10 + 5 x 50 = 300 (5 filas de 1s y 5 filas de 5s), pero 300 no es divisible por 8. En consecuencia, no se puede embaldosar el tablero cuadrado 10 x 10 con L-tetraminós. Ingeniosa, ¿no?

Bibliografía
1.- Solomon W. Golomb, Polyominoes, Princeton University Press, 1994.
2.- George E. Martin, Polyominoes, a guide to puzzles and problems in tiling, The Mathematical Association of America, 1996.
3.- Tetris (wikipedia)
4.- Raúl Ibáñez, Los anuncios Tetris, primera parte (Las matemáticas en la publicidad, divulgamat)
5.- Raúl Ibáñez, Los anuncios Tetris, segunda parte (Las matemáticas en la publicidad, divulgamat)
6.- Miodrag S. Petkovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
7.- D. Fuchs, S. Tabachnikov, Mathematical Omnibus, AMS, 2007.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica



Hitos en la red #30 | Naukas
[…] Hablando de matemáticas, decía Tim Gowers (ganador de una medalla Fields él también en 1998), que existen dos culturas matemáticas, la de los constructores de teorías y la de los solucionadores de problemas. Lo segundo parece que encaja bastante con lo que hace Raúl Ibáñez en Tetris, embaldosados y demostraciones. […]
¡Feliz 2017, número de poliominós convexos por columnas! | Cifras y teclas
[…] conocías, seguro que los poliominós te han recordado al famoso juego del Tetris; te recomiendo esta entrada de Raúl Ibáñez en el Cuaderno de Cultura Científica para aprender más al […]
Enrique
Muy interesante el articulo.
Proyecto Tetris | Blog de Aula de Pantaleón Hernández Rodríguez
[…] Tetris y matemáticas […]
Jugamos al tetris | Blog de Aula de Pantaleón Hernández Rodríguez
[…] https://culturacientifica.com/2014/08/13/tetris-embaldosados-y-demostraciones/ […]
Los embaldosados de Truchet y el puzzle del diamante — Cuaderno de Cultura Científica
[…] patrones de embaldosado o teselado es un interesante tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. En la entrada de hoy del Cuaderno de Cultura Científica vamos a […]
Cuadrados mágicos geométricos — Cuaderno de Cultura Científica
[…] construye un triominó, o trominó, con cuatro cuadrados se tiene un tetraminó (véase la entrada Tetris, embaldosados y demostraciones), con cinco un pentominó, y así se puede continuar para cualquier número de […]
El rompecabezas IQ-Block — Cuaderno de Cultura Científica
[…] y rompecabezas geométricos, como el juego de los pentominós y sus derivados (véase la entrada Tetris, embaldosados y demostraciones), el Tetris o el Vee-21 (véase la entrada Embaldosando con L-triominós (Un ejemplo de […]
Conjuntos de baldosas auto-embaldosadas — Cuaderno de Cultura Científica
[…] leer las entradas Embaldosando con L-triominós (Un ejemplo de demostración por inducción) y Tetris, embaldosados y demostraciones). Sin embargo, las figuras geométricas de la retícula pueden ser otro tipo de poliformas, como […]