Cuando era un niño, los reyes magos me regalaron un cinExin con una humilde colección de pequeñas películas, entre las que se encontraba “Charlot atleta”. Me divertí enormemente con este cortometraje, pasándolo hacia delante, hacia atrás, a cámara lenta, rápida, o parándolo para buscar posiciones extrañas.


El tema de la entrada de hoy de la sección Matemoción del Cuaderno de Cultura Científica me ha hecho recordar esos momentos maravillosos de mi infancia que pasé viendo este corto, así como muchos otros, de uno de los grandes del cine, Charlie Chaplin (1889-1977), y de su entrañable personaje “Charlot” (en inglés “The Little tramp”, el pequeño vagabundo). Por ese motivo, hemos titulado esta entrada “Pi atleta”, en homenaje a uno de los más grandes cineastas de todos los tiempos (que realizó grandes películas como “Tiempos modernos”, “La quimera del oro” o “El gran dictador”). Pero no vamos a hablar de Charlot, ni del cine, sino del atletismo y más concretamente, de las pistas donde se celebran sus competiciones, y la relación de estas con el número pi.

Todas las personas que hemos practicado el atletismo, pero también todas aquellas a las que les gusta ver las competiciones de este ancestral deporte, ya sea por la televisión o a pie de pista, saben que en algunas de las pruebas, como por ejemplo 200 metros o 400 metros (lisos o vallas), los atletas no salen todos a la misma altura de la pista (como puede verse en la anterior imagen), para compensar que las calles exteriores tienen más recorrido que las calles interiores. En la entrada de hoy vamos a realizar un sencillo cálculo, con el número pi, para saber cuál es la ventaja que debe de tener el atleta de la calle 2 sobre el de la calle 1, así como la ventaja del resto de corredores, para que todos recorran la misma distancia.
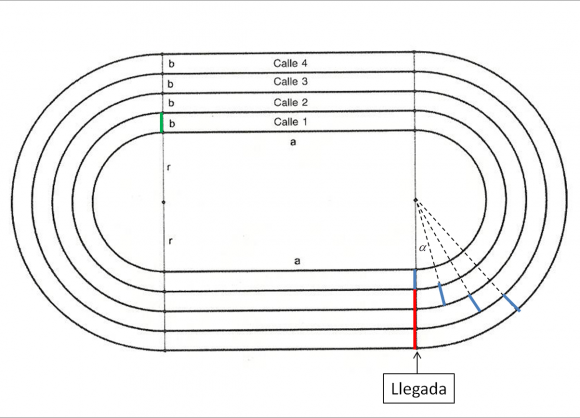
Como se puede ver en la imagen anterior, una pista de atletismo está formada por dos tramos rectos paralelos y dos tramos semicirculares que unen esos dos tramos rectos, formando así un circuito cerrado por el que correrán los deportistas. Según la IAAF, International Association of Athletics Federations, y también podemos leerlo en la página de la RFEA, Real Federación Española de Atletismo, el recorrido estándar de una vuelta al circuito es de 400 metros (que será la distancia que realiza el atleta que va por la calle número 1), la longitud de los tramos rectos podría ser de 100 metros con lo cual cada uno de los cuatro tramos del circuito tendría la misma longitud, aunque según la IAAF en la actualidad se considera que la medida estándar de los tramos rectos debe ser de unos 85 metros, la anchura de cada calle es de aproximadamente 1,25 metros y las medidas del recorrido que realizan los atletas se toman a 20 centímetros (0,2 metros) desde el borde interno de cada calle (para la primera calle se toman a 0,3 metros, pero en esta entrada consideraremos que en todas las calles es la misma distancia). Las medidas que acabo de presentar son realmente aproximaciones de las medidas reales con el objetivo de simplificar los cálculos que tenemos que realizar.
La cuestión que nos planteamos por lo tanto aquí es la siguiente:
¿Cuál es la ventaja de salida, que denotaremos por v, de cada corredor respecto del corredor de la calle 1?
Al efectuar el sencillo cálculo que nos dará la solución a la cuestión anterior, también contestaremos a la pregunta de cuál es el radio de cada una de las partes semicirculares para que la calle 1 tenga una longitud de 400 metros.
A continuación, vamos a calcular la longitud de cada una de las cuatro calles del esquema de pista anterior, y lo vamos a hacer en general para una pista cuyos tramos rectos tengan a metros (en el caso estándar sabemos que a es aproximadamente 85 metros) y la anchura de cada calle sea de b metros (en el caso estándar 1,25 metros). Recordemos que las medidas del recorrido de cada calle se toman a 0,2 metros del borde interior.
Para dicho cálculo solo hemos necesitado conocer la sencilla fórmula de la longitud de una circunferencia de radio r, . A partir de esta simple operación ya podemos calcular el radio r de las partes semicirculares. Despejando r de la primera ecuación (la calle 1 tiene una longitud de 400 metros) se obtiene que su valor es
Si los tramos rectos de la pista de atletismo midieran 100 metros, entonces el radio de las partes semicirculares valdría 31,63 metros, pero para los “85 metros” estándar, el radio vale aproximadamente 36,4 metros.
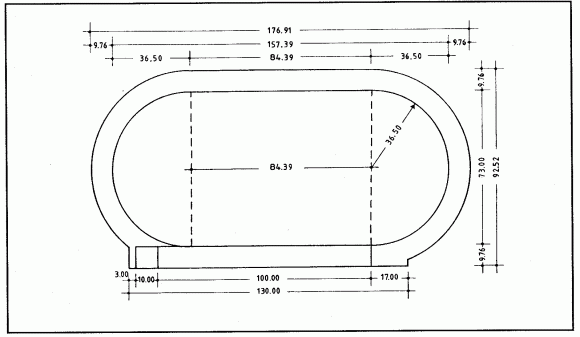
El hecho de diseñar una pista con tramos rectos más cortos, hace que la pista sea algo más ancha, y en conjunto las instalaciones de atletismo más “cuadradas” (es decir, menos alargadas y más anchas), lo cual es más conveniente para la constructibilidad del complejo deportivo. Además, con tramos rectos de 85 metros, se dispondrá de más espacio en el interior. El área de la zona interior se puede calcular fácilmente, . Por lo tanto, la superficie del interior es igual a:
A(100) = π x 31,632 + 2 x 31,63 x 100 ≈ 9.469 m2
A(85) = π x 36,42 + 2 x 36,4 x 85 ≈ 9.949 m2
Pero volvamos al problema inicial planteado, es decir, el cálculo de la ventaja de salida de los corredores de cada una de las calles respecto al atleta de la calle número 1, en la prueba de 400 metros (lisos o vallas). Como para esta prueba hay que dar una vuelta entera, el cálculo realizado anteriormente de la longitud de una vuelta para cada una de las calles de la pista de atletismo es suficiente para dar respuesta a la cuestión. Comparando la longitud de las calles número 1 y 2, se observa que la segunda excede a la primera en metros, luego esa es la ventaja de la calle 2. La ventaja de la calle 3 será
y la de la calle 4,
.
En consecuencia, la ventaja de cada una de las calles en la prueba de 400 metros no depende de la longitud del tramo recto y su valor es
v2 = 2πb ≈ 7,85 m ; v3 = 4πb ≈ 15,71 m ; v4 = 6πb ≈ 23,56 m

A la hora de trazar las marcas de salida de cada uno de los corredores en la prueba de los 400 metros se puede hacer tomando las medidas sobre la pista (a 20 centímetros del borde interior) y pintando las marcas apuntando al centro de la semicircunferencia. Pero también, se pueden realizar conociendo el ángulo entre la marca de la calle número 1, dada por la vertical desde el centro de la semicircunferencia, y la marca de cada una de las demás calles (véase el esquema anterior de una pista de atletismo con cuatro calles), y después utilizar un par de cuerdas sujetas en el centro de la semicircunferencia, la primera marcando la vertical de la marca de la calle número 1 y la otra formando un ángulo
(para lo cual puede ser útil un teodolito) con la anterior.
Pero la cuestión es cómo saber el ángulo entre la marca de la calle número 1 dada por la vertical desde el centro de la semicircunferencia y la marca de cada una de las demás calles, por ejemplo, de la calle número 2. La respuesta es la fórmula de la longitud de un arco de circunferencia de ángulo
, siendo su radio
, es decir,
. Como hemos calculado anteriormente las ventajas, es decir, las longitudes de los arcos, y el radio
, entonces los ángulos valen
Para dar respuesta a la cuestión planteada en esta entrada del Cuaderno de Cultura Científica sobre las ventajas de los corredores respecto al atleta de la calle número 1, solamente hemos necesitado hacer uso de la sencilla fórmula de la longitud de arco de una circunferencia. Pero lo importante no es si las matemáticas utilizadas son sencillas, sino si hemos resuelto el problema real que nos habíamos planteado inicialmente.
Referencias:
1.- Alfred S. Posamentier, Ingmar Lehmann, La proporción transcendental, la historia de pi, el número más misterioso del mundo, Ariel, 2006.
2.- IAAF, International Association of Athletics Federations, www.iaff.org
3.- RFEA, Real Federación Española de Atletismo, www.rfea.es
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica




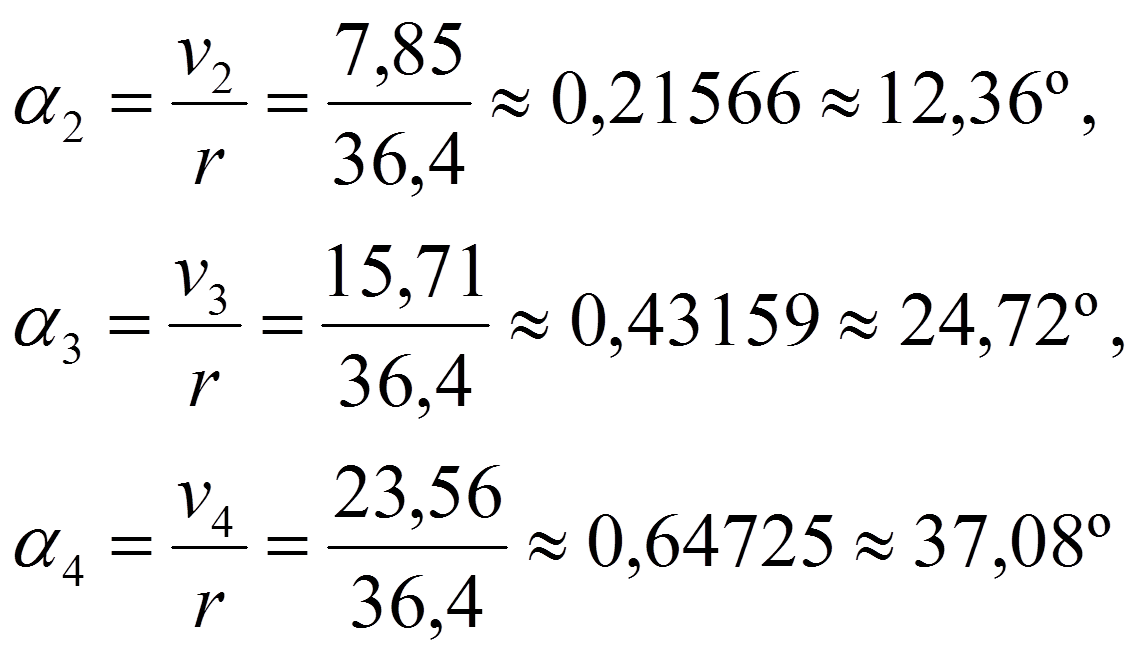

¿Es normal el número pi? – Cuaderno de Cultura Científica
[…] Parte de la magia de este número es que aparece en los lugares más insospechados, y tiene infinidad de aplicaciones, aunque como muchas otras constantes matemáticas. En todas las ramas de las matemáticas, desde la geometría hasta la probabilidad, pasando por la teoría de números, en física (en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb de la electricidad), en geología (para estimar la longitud de los ríos, debido a que relaciona dicha longitud con la distancia directa del nacimiento del río a su desembocadura), en bioquímica (en el estudio de la estructura de una molécula de ADN), en astronomía (en la búsqueda de exo-planetas o el estudio de la forma del universo), y muchas aplicaciones más en navegación, análisis de señales, dinámica de poblaciones o ingeniería, incluso en deportes (para calcular las posiciones de salida en las pistas de una carrera de atletismo, como vimos en la entrada Pi atleta). […]
Zarahy Baleria Achipiz Vitoviz
No veo la imagen de la pista atlética