Mi última entrada en el Cuaderno, Pitágoras sin palabras, estuvo dedicada al Teorema de Pitágoras y a una serie de demostraciones visuales del mismo.

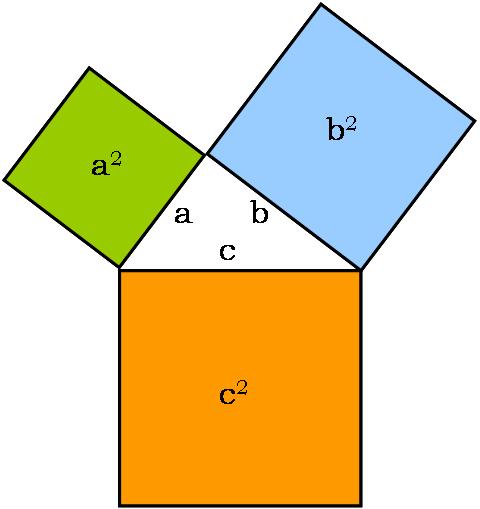
Comenzaba el artículo comentando que sin lugar a dudas el teorema conocido en la Edad Media como Inventum hecatombe dignum (invento digno de una hecatombe), es el resultado matemático más conocido en nuestra sociedad. Casi con total seguridad, la mayor parte de las personas lo citarían si se les preguntase por un resultado matemático e incluso me atrevería a afirmar que la mayoría de ellas serían capaces de recordar su formulación, es decir, que “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos” o en su versión más algebraica, que a²+b²=c², si a y b son los catetos y c la hipotenusa del triángulo rectángulo. Así mismo, el peso social y cultural de este teorema ha sido de tal magnitud quese ha convertido no solamente en un símbolo de las matemáticas, las escolares y las no escolares, sino también de la educación.

Por esta razón, parece lógico pensar que el Magister matheseos (como es conocido desde la Edad Media, debido a que para ser docente se solía exigir un conocimiento destacado del mismo, e incluso que el candidato presentase una nueva demostración) forme parte de nuestra cultura, y que por lo tanto, aparezca en sus diferentes manifestaciones, artes plásticas, literatura, música, cine, publicidad, etc. Con el presente artículo se inicia una serie en la que se pretende mostrar la presencia del Teorema de Pitágoras en algunas manifestaciones culturales.

Y empezaremos por las artes plásticas. Mostraremos cómo algunos artistas plásticos actuales han reflexionado sobre este resultado geométrico y lo han utilizado en sus pinturas y esculturas. Hemos de tener muy en cuenta el esquema geométrico anterior, puesto que muchos de ellos lo utilizan para representar el resultado matemático.

Iniciaremos este paseo con el artista conceptual norteamericano Mel Bochner (Pittsburg, 1940), quien a lo largo de su carrera artística ha realizado una interesante y continua reflexión sobre las matemáticas, y en particular, sobre la geometría. La primera de sus obras que traemos a este espacio es “Teorema de Pitágoras (cuadrado rojo)” de 1973, la cual efectivamente tiene el esquema anterior como centro de la obra.

Mel Bochner, Teorema de Pitágoras (cuadrado rojo), 1973

Esa pintura fue el germen de una serie de composiciones posteriores que también tenían al resultado geométrico como elemento principal, entre ellas este “Pitágoras (4)” que se muestra aquí.

Mel Bochner, Pitágoras (4), 2006

Otra línea de trabajo de Bochner fue la desarrollada en obras como “Meditación sobre el Teorema de Pitágoras” de 1972 (realizada con avellanas y tiza sobre el suelo). Esta obra fue utilizada como portada de la revista The College of Mathematics Journal en 2009 y creó cierto revuelo en la comunidad matemática, ya que algunos matemáticos pusieron de manifiesto que había algunas contradicciones en relación al Teorema de Pitágoras.

Mel Bochner, Meditación sobre el Teorema de Pitágoras, 1972

Esta obra, que reflexiona sobre este importante elemento de la cultura occidental, tenía como punto de partida la igualdad algebraica que subyace al teorema de Pitágoras, a²+b²=c², y a la terna pitagórica utilizada como ejemplo universal, (3, 4, 5), es decir, 3²+4²=5² (9+16=25). Si nos fijamos en la imagen, los cuadrados tienen 9, 16 y 25 avellanas (al permitirse contar las avellanas de los vértices del triángulo rectángulo en los dos cuadrados en los que están, lo cual fue una acertada decisión del artista en beneficio del resultado visual final).

La crítica de parte de la comunidad matemática es que al poner las avellanas sobre el esquema geométrico típico, el triángulo rectángulo dibujado en tiza blanca resulta no ser realmente un triángulo rectángulo, ya que sus catetos miden 2 unidades (siendo una unidad la distancia entre avellana y avellana) y 3 unidades, mientras que su hipotenusa mide 4 unidades, terna que no verifica el teorema de Pitágoras 2²+3² = 13 ¹ 16 = 4², y por tanto, el triángulo (2, 3, 4) no es rectángulo. Efectivamente, esto es cierto, aunque no comparto la crítica. En mi opinión, la obra de Bochner es una bella y sugerente pieza de arte, que como el mismo dice es una meditación (artística y personal) del Teorema de Pitágoras, y no una ilustración del mismo.

Mel Bochner ha seguido trabajando sobre esta misma idea hasta la actualidad, utilizando también otros materiales, como piedras, fichas del Go o cristales.

Nuestra siguiente visita es a una artista norteamericana que se define como “artista conceptual que trabaja con las matemáticas”, Marion Drennen. Entre sus principales temas de interés están los números, las proporciones, las matemáticas en general y la física cuántica. Una de sus obras es “Homenaje a Pitágoras” (2006), en la cual podemos ver como elemento central de la obra el diagrama geométrico del Teorema de Pitágoras. En esta obra se alude a otros aspectos importantes de la matemática pitagórica, como es la frase “Number rules the Universe” (el número gobierna el universo), la palabra “Proof” (demostración), puesto que fue Pitágoras quien introdujo la necesidad de dotar de una demostración rigurosa y lógica a los resultados matemáticos, los números Phi y raíz de dos, la espiral áurea, el pentágono o las proporciones musicales, entre otros.

Marion Drennen, Homenaje a Pitágoras, 2006

Y siguiendo en EEUU, Lun-Yi Tsai es un artista y matemático, que se formó académicamente tanto en Matemáticas como en Bellas Artes, que enseña matemáticas en la Universidad de Miami y que desarrolla un arte alimentado de esas ideas matemáticas con las que también trabaja. Pero más aún, el suyo es un arte muy especial, que ilustra y reflexiona sobre conceptos y resultados matemáticos modernos (variedades diferenciables, espacio tangente, fibración de Hopf, el teorema del punto fijo de Brouwer, etc). Tras su formación académica estuvo 6 años haciendo arte en China, y después pasaría por Berlín como artista de la Karl Hofer Gesellschaft, para volver finalmente a EEUU, donde ahora es Profesor del Departamento de Matemáticas (U. Miami). La obra que mostramos aquí es “Change” (2008), que muestra la demostración geométrica de Euclides del Teorema de Pitágoras. Compárese esta obra con el esquema que aparece en “Los Elementos” de Euclides y que mostramos también aquí. Además, el cuadro es anterior a las elecciones presidenciales de EEUU, que Barack Obama, que aparece en el cuadro, ganaría convirtiéndose en el primer presidente negro de EEUU.

Lun-Yi Tsai, Cambio, 2008

Esquema de la demostración de Euclides del Teorema de Pitágoras

El siguiente artista también es estadounidense, Marcus Zilliox (Gila River Pima Community, Arizona, 1972), descendiente de nativos americanos y mexicano-americanos. Realizó en 2012 una serie de trabajos inspirados en el Teorema de Pitágoras, bajo el título “Geometrical explorations”, y que toman el esquema geométrico anterior del Teorema de Pitágoras como un elemento principal y motivador de la obra. Aquí mostramos algunas de las obras.

Marcus Zilliox, Crossing

Marcus Zilliox, Fuente, Versión pitagórica (después de Duchamp)

Marcus Zilliox, Hephaestus

Marcus Zilliox, Escultura del Teorema de Pitágoras

El escultor y profesor de humanidades de la Universidad Bryant en Rhode Island (EEUU) William P. Haas utiliza la demostración geométrica de Bhaskara (véase Pitágoras sin palabras) para realizar su escultura “La visión de Pitágoras”, como podemos apreciar mirando al cuadrado horizontal central realizado en madera, con sus correspondientes triángulos rectángulos y el cuadrado central, que al mismo tiempo tiene un esquema similar en pequeño.

William P. Haas, La visión de Pitágoras (1993)

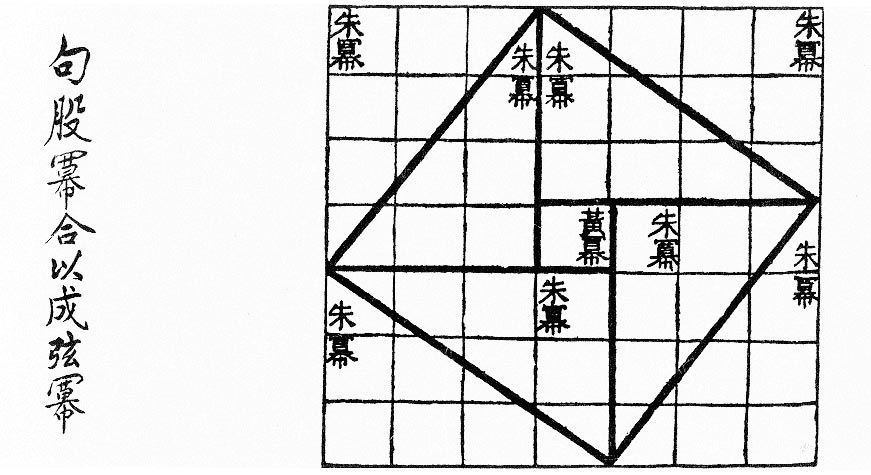
En la siguiente obra de La pintora de Minneapolis Stella Pinilla, titulada “Homenaje a Pitágoras”, nos encontramos un esquema similar al anterior, pero claramente inspirado –quizás también el anterior- en la demostración china de tipo gráfico-experimental del Teorema de Pitágoras para el triángulo concreto (3, 4, 5), que aparece en el texto clásico chino Chou-Pei Suan-Ching (aritmética clásica del gnomon y estudio de las órbitas circulares en los cielos), y que mostramos también aquí.

Stella Pinilla, Homenaje a Pitágoras

Chou-Pei Suan-Ching (hacia el 300 a.n.e.)

Si dejamos Estados Unidos, nos encontramos por ejemplo con el pintor, fotógrafo y cineasta chipriota, Ronis Varlaam, que tiene al menos dos obras sobre el Teorema de Pitágoras. Una es “A walk in Margate”, con el esquema habitual del Teorema de Pitágoras en amarillo-rojo-azul, quizás haciendo una referencia a que este teorema recoge la esencia del concepto de distancia euclídea en un plano, mientras que el otro “El Teorema de Pitágoras, una versión alternativa”, en la que se sustituyen los cuadrados amarillo-rojo-azul por círculos, los cuales para que tengan el mismo área que los correspondientes cuadrados tienen que tener un diámetro igual al correspondiente lado del triángulo multiplicado por 2 y dividido por la raíz de pi (como puede verse con la sencilla fórmula del área de un círculo).

Ronis Varlaam, A walk in Margate

Ronis Varlaam, El Teorema de Pitágoras, una versión alternativa

Serge Doubovetzky es un ingeniero retirado y pintor francés de origen ruso, que descubrí gracias a la revista francesa Tangente (n. 23, 2005), cuyo arte también está profundamente relacionado con las matemáticas. Mostramos aquí su obra “Pitágoras 2”.

Serge Doubovetzky, Pitágoras 2

Cambiemos un poco de tipo de arte y adentrémonos en una obra perteneciente a lo que se conoce como arte masónico. La imaginería de la masonería tiene mucho que ver con la geometría clásica, y suele incluir objetos como la escuadra y el compás, pero también el Teorema de Pitágoras, como en el dibujo del artista alemán Jens Rusch de título “Pitágoras”.

Jens Rusch, Pitágoras

Y para terminar, un precioso cuadro del artista uruguayo D. Amaral Oyarvide, “Pitágoras, demostración del teorema”…

D. Amaral Oyarvide, “Pitágoras, demostración del teorema”

Sobre el autor: Esta anotación ha sido realizada por Raúl Ibáñez, profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica