Los que ya tenemos una cierta edad, recordamos con cariño un videojuego llamado Los Lemmings.

En este juego de niveles, unos seres de pelo verde y vestidos azules salen de un portal para caminar inexorablemente en la misma dirección hasta encontrar un obstáculo insalvable, en cuyo caso cambian de sentido. El objetivo del juego era conducirlos a la salida, salvando los obstáculos. Para ello, se podía asignar a determinados lemmings un oficio (parar al resto de lemmings, cavar en horizontal, vertical o diagonal, explotar…). Pero uno de los oficios que más llamó mi atención es el de Constructor. Este ser se dedicaba a construir una escalera con bloques idénticos (creo recordar que eran 12). Cada bloque (más o menos) se situaba medio fuera del inmediatamente anterior.

Y claro, mi joven mente ya apuntaba maneras y pensaba… ¿cómo diablos se mantiene en pie esa escalera si el bicho no usa cemento? La respuesta es… ¡Esto es un videojuego, no la vida real; aquí no hay gravedad para las escaleras!

Pero esta respuesta no me satisface. Así que os voy a plantear un problema. Imaginad que sois Lemmings Constructores y que disponéis de una cantidad indefinida de bloques todos idénticos, pongamos que de longitud 1 cm. Necesitáis salvar un abismo de 2 cm para llegar a la salida. Si no disponéis de cemento (ya es mala suerte, tener una infinidad de bloques, pero nada de cemento…) y la fuerza de la gravedad (ramera inexorable) la tenemos en cuenta (no como en el juego), ¿seréis capaces de construir una escalera que salve el abismo? Y si sois capaces… ¿cuántos bloques necesitaréis?

Este problema, que en la literatura se conoce como “El Problema del apilamiento de libros” (“The Book Stacking Problem”, en inglés) parece una tontería, pero es una de esas cosas que cuando las ves resueltas te dejan con la boca abierta. Para resolverlo sólo hay que saber un poquitín de física y algo más de matemáticas. Vamos allá.

La parte física que necesitamos saber es el concepto de centro de masas. Dado un objeto, el centro de masas es un punto en el que si concentramos en el toda la masa del objeto, el punto y el objeto tendrán las mismas propiedades dinámicas (vamos que se moverán igual y seguirán la misma trayectoria si le aplicamos fuerzas idénticas). Si el objeto suponemos que está muy bien hecho y tiene densidad constante, el centro de masas coincide con el centro geométrico del objeto. Así, si pensamos en bloque tipo ladrillo, el centro de masas estará justo en medio del bloque… ahí mismo:

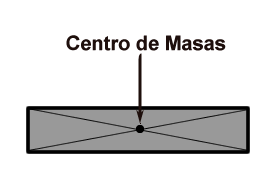
Muy bien. Pero… ¿qué pasa si tenemos varios objetos juntos (como nuestros bloques apilados) cada uno con su centro de masa? ¿Cuál es el centro de masas combinado de 2 objetos? Si tenemos un objeto con masa cuyo centro de masa está en la posición (horizontal) y un segundo objeto de masa cuyo centro de masa está en la posición (horizontal) , el centro de masas combinado se encuentra en la posición

Pues creo que ya hemos recordado toda la física que necesitamos. Vamos a atacar nuestro problema.

Vamos a colocar uno de nuestros bloques en el borde izquierdo del abismo. Para que el bloque no caiga, hace falta que el centro de masas esté aún sobre el suelo. Para conseguir la máxima distancia, podemos colocar el bloque de forma que el centro de masas esté justo en el borde del abismo. Así tendremos 1 bloque en equilibrio (inestable, pero equilibrio) y sobresaldrá una distancia del borde.

Pongamos un segundo bloque. Es evidente que no lo podemos poner arriba (así no ganaríamos distancia) por lo que hay que ponerlo debajo. Pensemos que ponemos el segundo bloque justo pegado al borde del abismo, donde establecemos el 0 del eje horizontal.

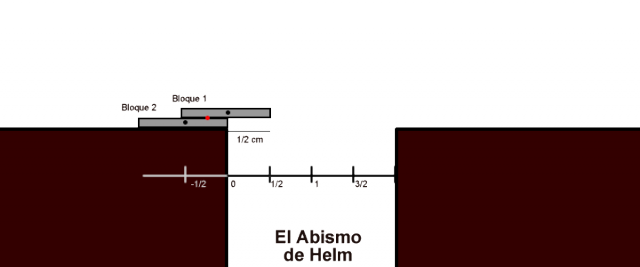
Calculemos la posición del centro de masas del conjunto de dos bloques (pongamos de masa ):

Así que podemos desplazar los dos bloques justo 1/4 cm para que el centro de masas combinado caiga justo en el borde y no caiga. De esta forma, el borde del conjunto de dos bloques estará a una distancia del borde del abismo.

Ya que hemos puesto 2, vamos a poner el tercer bloque. Hagamos la misma construcción que antes y coloquemos el Bloque 3 justo por debajo y alineado con el borde del abismo. Pero para facilitar las cuentas, podemos suponer que todo el conjunto Bloque 1 y Bloque 2 es un único objeto de masa cuyo centro de masas está al borde del abismo.

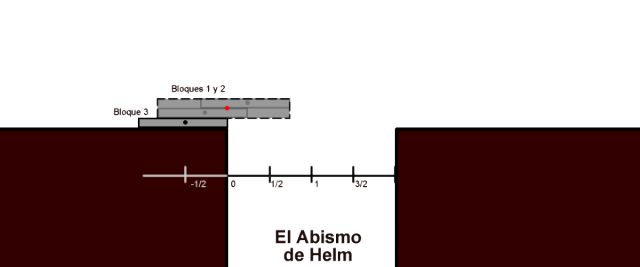
Calculemos ahora (la posición de) el centro de masas del conjunto de los 3 bloques:

Pues ya sabemos que podemos empujar los 3 bloques 1/6 cm y el conjunto de 3 bloques seguirá en equilibrio. La distancia a la que hemos llegado es .

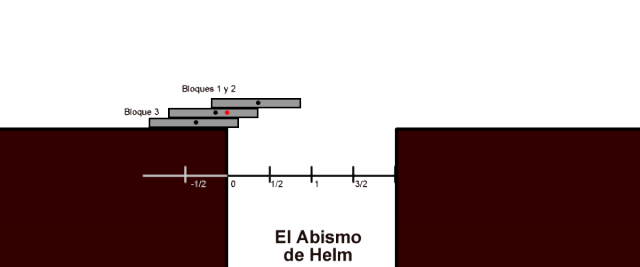
Vamos a dar un salto cualitativo. Pensemos que ya hemos colocado bloques con los que nos hemos desplazado una distancia y tratemos de poner el Bloque de la misma forma que antes.

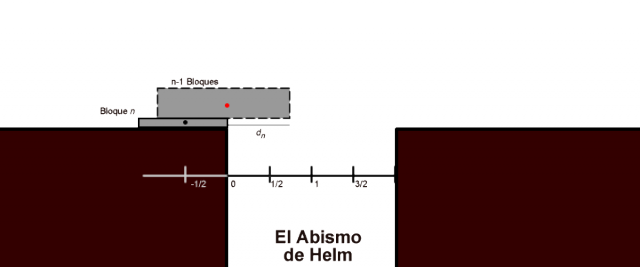
Si calculamos ahora la posición del centro de masas combinado de los bloques resulta que

Luego en la etapa enésima podemos desplazar todos los bloques 1/2n cm y seguirán estando en equilibrio. De esta forma, alcanzaremos una distancia .

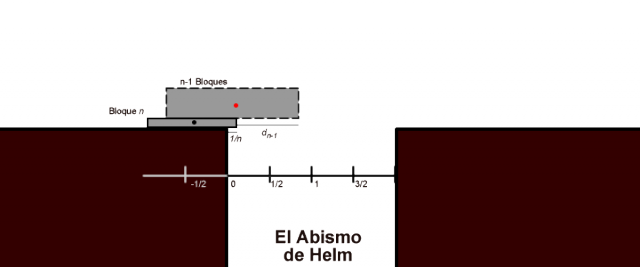
Pero entonces… ¿cuánto nos hemos desplazado en total? Hagamos la cuenta. Sabemos que , pero de igual modo, y así sucesivamente hasta llegar a . Por lo tanto

Y esa suma que está en el paréntesis, en matemáticas se conoce como Número Armónico (y suele denotarse por ).

Ya hemos acabado con la parte física. Pasemos a las Matemáticas.

¿Cuánto puede llegar a valer esos números armónicos? Un sencillo resultado (que suele verse en un primer curso de cálculo de cualquier carrera científica o técnica) nos dirá que… ¡TAN GRANDE COMO UNO QUIERA!

¿Cómo?

Pues eso que acabas de leer. Dime un número, tan grande como se te ocurra, que yo seré capaz de darte un número armónico más grande que el tuyo. Esto se conoce como divergencia de la serie armónica. Vamos, que con una cantidad suficiente de bloques, podremos salvar el abismo.

¿Pero cuántos bloques necesitaremos para salvar el abismo del problema que nos planteamos? Vamos a echar unas cuentas. En la siguiente tabla veis los valores de la distancia desde hasta .

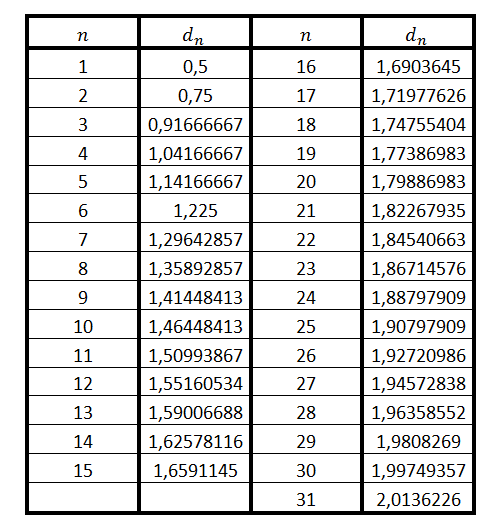
Como podéis comprobar, el 4º bloque ya está totalmente fuera del borde del abismo (1 cm). Pero para llegar al otro extremo (2 cm), necesitamos 31 bloques.

Pero ya que estamos… vamos a ponernos exageraos (o como se dice en mi tierra, “sagerao”). Supongamos que los bloques son de 1 metro de longitud, algo más propio para el ser humano. ¿Cuántos de estos bloques necesitamos para superar… (qué te digo yo)… el Río Guadalquivir a su paso por Sevilla? Como referencia, el Puente de Triana mide 149 metros, por lo que podemos suponer que el ancho del río es de unos 100 metros.

Para resolver este nuevo “embolao”, necesitamos algo de matemáticas más avanzadas. Resulta que para valores muy grandes de , el número armónico se comporta más o menos como , donde es la Constante de Euler-Mascheroni y vale, más o menos, 0,557.

Con este hecho de nuestro lado, cualquier programa de cálculo simbólico nos dirá que para conseguir que superar el Estrecho necesitaremos del orden de bloques para llegar al otro lado. Por muy finos que éstos sean (imaginemos que miden 1 micra), la altura alcanzada es… bueno, del orden de veces el diámetro del universo observable. Casi ná. Y es que los números armónicos se hacen cada vez más y más grandes, pero muy poquito a poco.

Con todo lo que habéis leído, ya sabéis Bloque a bloque podréis superar cualquier obstáculo. Eso sí, tendrá que ser con mucha paciencia y usando muchos bloques. No como los Lemmings, que en nuestra casa las escaleras respetan la Ley de la Gravedad.

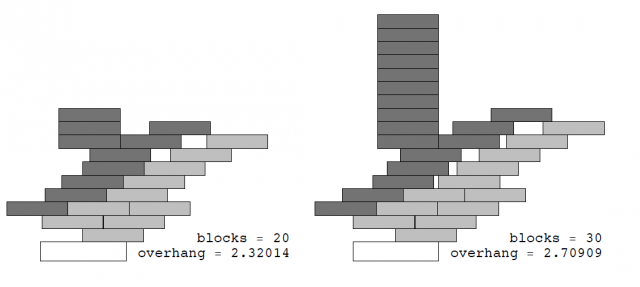
PD: Si queréis un poco más de rapidez, quizás la forma de escalera no sea la más adecuada. Puedes consultar el artículo Overhang [PDF] de Mike Paterson y Uri Zwick para las mejores configuraciones con diferentes números de bloques. Os dejo con las imágenes y los datos de las configuraciones óptimas con 20 y 30 bloques.

Este post ha sido realizado por Jose Antonio Prado Bassas (@Eliatron) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Para saber más:

Weisstein, Eric W, «Book Stacking Problem.» From MathWorld–A Wolfram Web Resource.

Bert G. Wachsmuth y Jillian Gaglione “The Leaning Tower of Lire.”

Manuel Díaz Escalera, “Escalera hacia el cielo.”

Nick Berry, “Hangover.”

Cazelais, “Block stacking problema.”