Eva Ferreira
La última crisis ha generado inumerables opiniones acerca del sistema financiero, despachándose por doquier críticas al mismo, a los famosos derivados, -esos productos endiabladamente complicados-, y a la regulación de los mercados, entre otras. Las matemáticas utilizadas no han quedado exentas de crítica. De hecho, encontramos expresiones en los medios como “El gran fracaso de los modelos matemáticos en el mundo de la inversión”, “Los físicos y matemáticos que hundieron Wall Street” o “La ecuación matemática que causó el derrumbe en el sector financiero” (La Vanguardia 17-02-2012)
Pero ¿estaríamos mejor sin el desarrollo matemático que se ha utilizado en la economía financiera? ¿Sería el mercado financiero menos sensible a la especulación?
Las matemáticas no resuelven por sí mismas los problemas generados por el sistema financiero. Las matemáticas actúan en finanzas como instrumentos de ayuda a la toma de decisiones pero no son, ni serán, bolas de cristal.
Es cierto que los modelos matemáticos han tenido un enorme impacto en el desarrollo del mercado de derivados. Un derivado es un activo cuyo valor en el futuro es una función de otro activo, que denominamos activo subyacente. Así, los agricultores llevan siglos realizando contratos derivados. El contrato entre un agricultor y su financiero consiste en que el financiero paga al agricultor un precio X fijado de antemano por la cosecha, independientemente de lo que suceda cuando se recoja. Si el valor final de la cosecha (el activo subyacente) es mayor que X, los beneficios son para el financiero, y si, por el contrario, el valor final es menor, también lo serán las pérdidas. Es decir, con este contrato derivado (un contrato futuro) el agricultor transfiere al financiero el riesgo del valor de su cosecha.
Otro tipo de derivados son las opciones. Una opción de compra es un contrato por el cual el propietario de la opción adquiere el derecho a comprar un cierto activo S en un momento T (fijado en el contrato) a un precio de ejercicio K, también fijado en el contrato. De nuevo, con la opción de compra estamos transfiriendo el riesgo que supone comprar la acción directamente y acotamos las posibles pérdidas.
Los modelos matemáticos de derivados proporcionan las herramientas para que, si se dan determinados supuestos, seamos capaces de poner precio a esos contratos derivados. En particular, Black, Scholes y Merton se preguntaron cuál debe ser el precio justo P de una opción de compra.
Así, imaginemos por un momento que no hay inflación, y que hemos pagado P por nuestra opción de compra, y sea ST el valor del activo en el futuro T. Si al llegar a T, ST > P + K, ejerceremos nuestro derecho, ya que hacerlo nos proporciona un beneficio, puesto que ST – P – K > 0. En otro caso, no merece la pena ejercer el derecho, ya que estaríamos pagando un precio mayor que el precio del activo en el mercado.
El gran logro de Fisher Black (matemático y economista), Myron Scholes (matemático y abogado) y Robert Merton (economista) fue determinar analíticamente la fórmula que valora esa opción en un mercado con dos activos, el activo libre de riesgo (cuyo precio en el futuro está determinado por el tipo de interés r) y el activo subyacente St. Eso sí, la fórmula, que acabó siendo merecedora del premio Nobel, se calcula bajo ciertos supuestos. La expresión de estos supuestos se puede realizar desde un enfoque de teoría financiera o como unos supuestos dentro del cálculo matemático bajo incertidumbre (cálculo estocástico):
1) Los rendimientos de los activos, sea cual sea el intervalo temporal en el que los calculemos, son variables aleatorias independientes y siguen una distribución normal. Formalmente, el proceso estocástico Stque rige la dinámica de los precios de los activos es un proceso geométrico browniano.
2) No hay posibilidades de arbitraje (no puede haber beneficios netos sin riesgo). Por tanto, productos que dan en T el mismo valor, deben tener el mismo precio hoy. Esto supone que los precios descontados por el interés libre de riesgo e-rt St , son un proceso martingala (i.e., su valor esperado condicionado a la información en un periodo s
3) Es posible recolocar posiciones de una cartera en tiempo continuo. Así, las carteras se pueden expresar como integrales estocásticas o transformadas de martingala, donde los procesos que definen el número de títulos de cada activo son procesos previsibles.
En este contexto, podemos diseñar una cartera de cobertura para cualquier producto derivado sobre St. Por tanto, el valor de esa cartera (conocido) debe ser igual al precio que debe tener el activo derivado.
Así, tenemos que el precio justo de una opción de compra en este contexto se obtiene mediante la fórmula de la izquierda,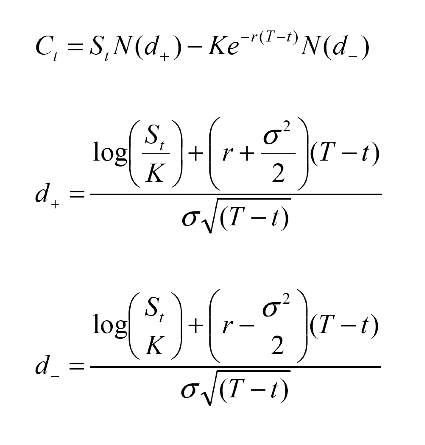 
donde todos los valores son conocidos al realizar el contrato, salvo s, que se estima a partir de datos de mercado.
Este resultado se publicó en el Journal of Political Economy en 1973, no sin dificultad porque, entre otras cosas, se consideró de dudosa utilidad lo que se veía como un mero pasatiempo matemático.
En 1972 se acababa de poner en marcha el mercado de opciones de Chicago (Chicago Board Options Exchange) y los operadores tradicionales se fiaban de su olfato para comprar y vender en un mercado con pocas operaciones. Sin embargo, hubo un antes y un después de la fórmula. Un discreto operador llamado John Meriwether comenzó a reclutar los llamados quants procedentes de las mejores universidades, y los derivados pasaron de ser unos instrumentos un tanto exóticos, movidos por mucho instinto y pocos datos, a mover billones de dólares con poco instinto y muchos datos. Esa nueva era de quants se afianzó después de su éxito en el crash del 87, donde sus posiciones contrarias al olfato de los grandes tahúres de la época, obtuvieron beneficios millonarios.
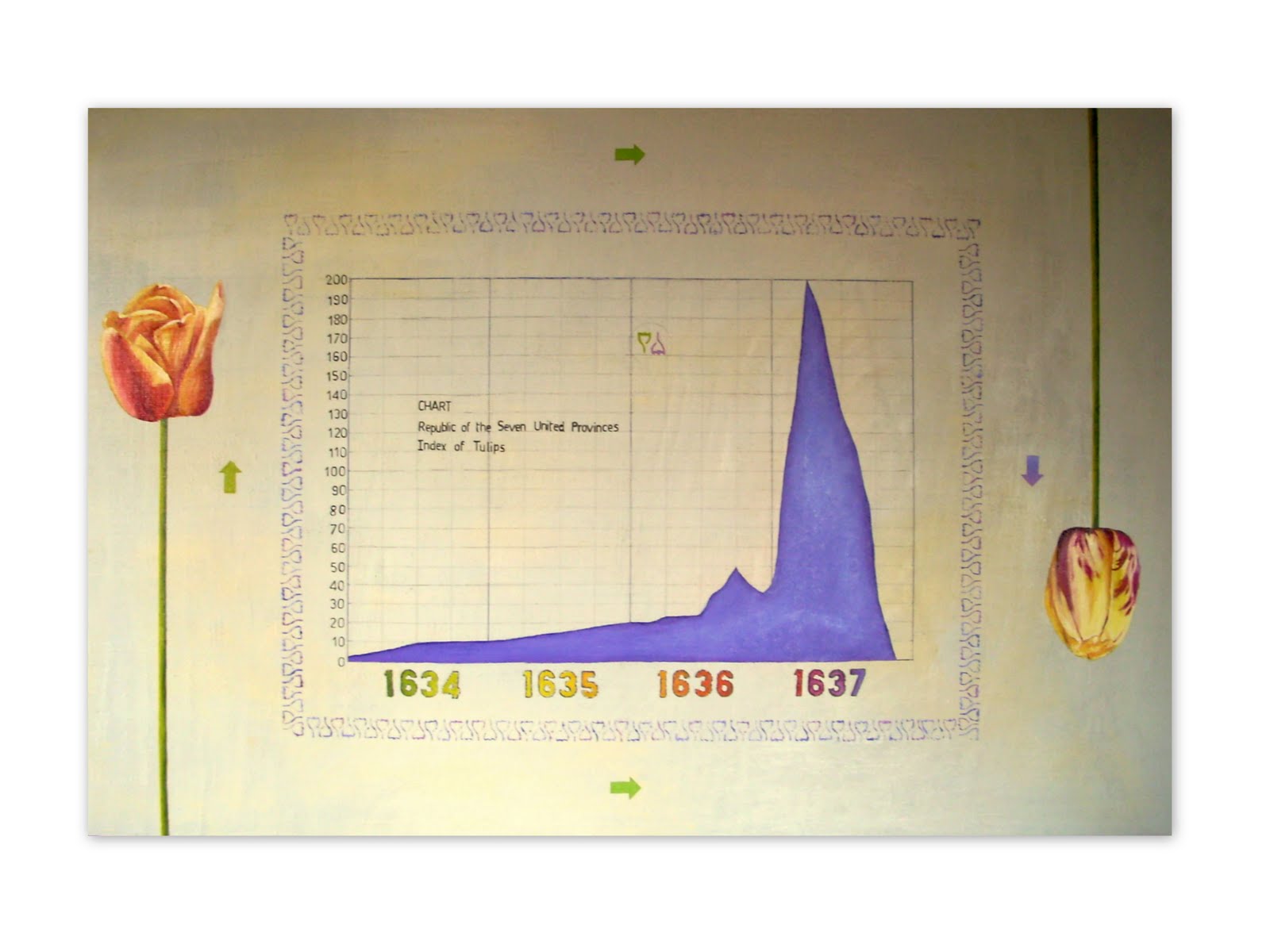
El estallido de la burbuja inmobiliaria en Estados Unidos, que motivó, a su vez, la caída en picado de los activos basados en hipotecas subprime, hizo que se pusieran en cuestión las nuevas formas de valoración de activos financieros. Sin embargo, los casos de uso abusivo y masivo de activos derivados con fines especulativos no son fruto de la sofisticación matemática; de hecho movimientos especulativos se han producido a lo largo de la historia y en mercados muy sencillos técnicamente. La crisis de los tulipanes, provocada por un mercado de futuros sobre bulbos de tulipanes, llevó a Holanda a la bancarrota en el siglo XVII. De la misma forma, los swaps promovidos para cambiar deuda pública a corto plazo por emisiones de la Compañía de los Mares del Sur a principios del siglo XVIII llevó Europa a una aguda depresión económica y sentó las bases para la Revolución francesa en 1789. El propio Isaac Newton perdió 20.000 libras por ello, y al respecto, más tarde llegó a declarar que “puedo predecir el movimiento de los cuerpos celestes, pero no la locura de las gentes”.
El cálculo estocástico no es una bola de cristal, pero proporciona una metodología para encontrar patrones en el comportamiento de los mercados financieros. Mejor que despedir a las matemáticas de su estudio y dejar que las reglas de la valoración sean un patrimonio oscuro y privado, es aprender de lo sucedido y mejorar la metodología. Tenemos retos, como profundizar en el estudio de modelos con colas pesadas, procesos multivariantes que recojan mejor la dependencia entre los activos, realizar estadística utilizando más información que los datos históricos de cada activo, o revisar la estimación del riesgo en que se basan las agencias de rating, entre otros.
El uso del cálculo estocástico ayuda a mejorar las vías del tráfico financiero y los vehículos que circulan por ella. Cuestión bien distinta es cuáles deben ser las normas para regular ese tráfico. Pero esta es otra historia y forma parte de otro relato.
—————————————————————————–
Sobre la autora: Eva Ferreira es catedrática de Economía Aplicada en la UPV/EHU
Antonio (AKA «Un físico»)
Ya es casualidad que en el brevísimo periodo de tiempo que sigo esta web, habéis tratado 4 temas totalmente diferentes entre sí; pero que a mí me vienen interesando tanto que me he decidido a escribir sobre ellos.
– Sobre el método científico (aplicado a la medicina), hice el pdf:
https://docs.google.com/file/d/0B4r_7eooq1u2dl9mTU5vNFJmc2M/edit
en el que ponía de manifiesto la importancia de la estadística.
– Sobre la selección natural, también tuve una discusión con alguien de ZK.
– Sobre la mecánica cuántica acabo de comentar algo con César.
– Y sobre el tema de esta última entrada … pues la verdad es que llevo meses dándole vueltas al asunto. Y yo creo que Doña Eva Ferreira no se hace la pregunta clave:
El modelo dinámico estocástico de Black -Scholes, ¿posee algún tipo de anomaía intrínseca que lo inhabilitaría para predecir, de forma general, los valores de compra-venta de los derivados financieros para los que inicialmente está diseñado (y por el que, recordemos, se logró el premio nóbel)?.
¿Y si la respuesta fuera que SÍ?. Precisamente me estoy leyendo un libro escrito por los catedráticos de la UPV/EHU: Alonso, Fernández y Gallastegui; que me ha dado un argumento fortísimo en favor de ese SÍ.
Cualquiera puede conseguir el email de la autora de esta entrada y ya me gustaría poder comentar con ella en privado o aquí en internet sobre este asunto.
Eva
Hola, efectivamente la ecuación se basa en supuestos que sabemos no se cumplen de forma general. Ello no impide que sea una herramienta útil y que nos ayude a entender el comportamiento de los derivados. Como digo en la entrada hay muchos retos para adecuar los modelos matemáticos a la realidad que observamos. En cualquier caso estos modelos nunca deben tomarse como una bola de cristal. Encantada de seguir debatiendo sobre este tema.
Antonio (AKA «Un físico»)
Muchas gracias por su respuesta, pero no me refería a la veracidad de los supuestos.
A mi me gustaría analizar el modelo Black-Scholes en profundidad. Como Nikolay en:
http://www.emis.de/journals/BAMV/conten/vol11/nikolay.pdf
pero sin meterme en esas disquisiciones noetherianas de las simetrías.
En las próximas semanas (¿meses?), escribiré mi propio pdf. Y como tengo su email de la EHU, volveré a contactar con usted.
Tal vez mi intuición lleve a algo importante (o … tal vez no), ya veremos.
De nuevo, muchas gracias.
Las matemáticas en Wall Street, ¿útiles o perversas? | Matemáticas y números | Scoop.it
[…] La última crisis ha generado inumerables opiniones acerca del sistema financiero, despachándose por doquier críticas al mismo, a los famosos derivados, -esos productos endiabladamente complicados-,… […]
Julián Álvarez-Santullano
¡-Magnífico-¡.-
Además, coincide con la opinión de este estudioso del Universo, y los modelos matemáticos que se usan actualmente, opinión que he resumido en una frase: CUIDADO CON LAS MATEMÁTICAS.-No las adoremos como un nuevo dios.-Es una poderosa HERRAMIENTA AUXILIAR, pero no nos conduce a la total verdad, SIEMPRE, y más especialmente, cuando no tenemos más remedio que incluir Probabilidades, simplificaciones, renormalizaciones, etc, etc. ante la enorme cantidad de factores influyentes en multitud de cuestiones-