La innovación más significativa de las matemáticas del siglo XVIII fue el concepto de función, expresado por Euler como cualquier relación razonablemente continua entre variables. Euler permitía que las funciones fuesen perfectamente generales, si bien en la práctica las constreñía a las relaciones geométricas y físicas.
Fue durante la segunda mitad del siglo XVIII que la definición de función se iría haciendo más general conforme los matemáticos iban descubriendo que muchas curvas o expresiones arbitrarias podían ser objeto de análisis. Alrededor del concepto de función el pensamiento matemático comenzó a disminuir su dependencia de las intuiciones geométricas y físicas.

El convulso comienzo del siglo XIX tuvo su reflejo en las ciencias en general y en las matemáticas en particular. Efectivamente, en el desarrollo de las matemáticas a comienzos de siglo la Revolución Francesa tuvo una gran importancia. Y es que Francia fue el centro de las nuevas matemáticas.

La École Polytechnique, fundada en 1794 como una escuela preparatoria para el ingreso en las escuelas de ingeniería como una forma de paliar la escasez de ingenieros tras la revolución, adquiriría renombre universal. El nuevo sistema universitario establecido por Napoleón entre 1806 y 1808, por el que se refundan las universidades y se crea el bachillerato como forma de acceso, crearía nuevas oportunidades profesionales para matemáticos y científicos, que pasarían a formar parte de la nueva nobleza meritocrática.

El área de investigación dominante, bajo el liderazgo de figuras como Joseph-Louis (conde de) Lagrange y Pierre-Simon (marqués de) Laplace, seguía siendo el cálculo y sus aplicaciones a la mecánica, pero una nueva generación vendría pronto a poner en cuestión todo ello y a construir nuevos métodos.
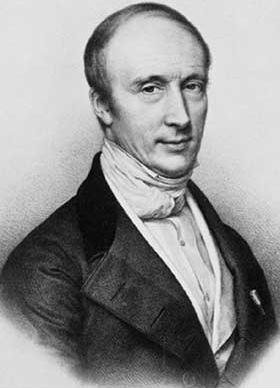
Las dos grandes figuras en la vanguardia de esta generación fueron Joseph (barón de) Fourier, con su matematización de la difusión del calor y sus métodos para encontrar soluciones basados en lo que conocemos hoy día como series de Fourier e integrales de Fourier, y Augustin-Louis (barón de) Cauchy, quien introduciría una aproximación al cálculo basada en el concepto de límite que sería la dominante en el futuro, iniciaría el análisis de variable compleja además de amplios tratamientos de la teoría de la elasticidad y la hidrodinámica.

Los trabajos de Fourier junto con los de Siméon-Denis (barón de) Poisson sobre electrostática constituyen las primeras matematizaciones importantes de fenómenos no mecánicos. La óptica de Augustin Fresnel y el electromagnetismo de André-Marie Ampère aparecieron poco después, ampliando la influencia de la física matemática definitivamente más allá de la mecánica.
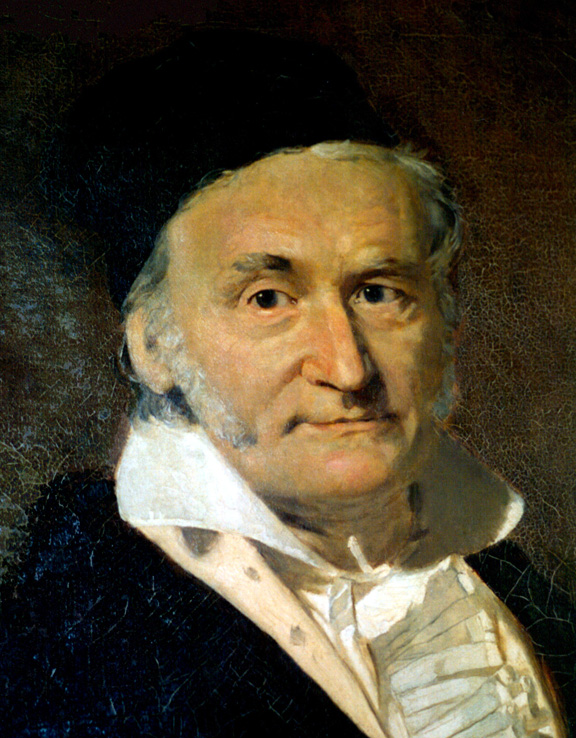
A partir de la década de los veinte las matemáticas se hacen más internacionales, resurgen el Reino Unido e Italia y, especialmente, Alemania, que estará en disposición de disputar la hegemonía a Francia cuarenta años después, en los sesenta. En buena medida responsable de ello fue un matemático que trabajó aislado en Gotinga la mayor parte del tiempo, Carl Friedrich Gauss, que inspiró a toda una generación de matemáticos alemanes al ser reconocidos sus logros internacionalmente. Su seguidor más importante, Bernhard Riemann, propuso una nueva versión de análisis de variable compleja y amplió el campo de la geometría más allá de la euclidiana. Riemann preparó el camino para, entre otros, Georg Cantor.

Gotinga fue el centro alemán de las matemáticas aplicadas, a diferencia de Berlín, donde se cultivaba la forma “más pura” de las mismas. Aquí, las clases de Karl Weierstrass, especialmente las de análisis real y (su versión de) variable compleja ejercieron una enorme influencia. Puede trazarse hasta estas clases la obsesión por el rigor que desde entonce caracteriza al pensamiento matemático.

La actitud “purista” de Berlín se extendería por Europa, incluida Francia, hasta el punto de que, a finales del XIX, el matemático más importante de Francia, Henri Poincaré, estaba prácticamente solo en sus estudios de física matemática.
—-
En la serie Apparatus buscamos el origen y la evolución de instrumentos y técnicas que han marcado hitos en la historia de la ciencia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Las matemáticas como herramienta (IV): D…
[…] La innovación más significativa de las matemáticas del siglo XVIII fue el concepto de función, expresado por Euler como cualquier relación razonablemente continua entre variables. […]
Hitos en la red #92 – Naukas
[…] reinterpreta el mundo, se va a otros mundos aunque se quede en este. Ya sea por las matemáticas, Las matemáticas como herramienta (IV): De la grandeur a las matemáticas puras, o el arte, Arte cartográfico, arte con mapas por Raúl […]
El genio de Ampère | Experientia docet | Cuaderno de Cultura Científica
[…] En este caso además no era ni siquiera necesario desarrollar nuevos equipos. Por eso, nada más conocerse la noticia, docenas de científicos en Europa y América comenzaron a realizar estudios intensivos sobre los efectos magnéticos de las corrientes eléctricas. De entre todos destaca el de André-Marie Ampère. Ampére, a quien James Clerk Maxwell se referiría como el “Newton de la electricidad”, terminaría construyendo con el tiempo una teoría completa de la electricidad y el magnetismo de base matemática. […]
Las matemáticas como herramienta (IV): D…
[…] La innovación más significativa de las matemáticas del siglo XVIII fue el concepto de función, expresado por Euler como cualquier relación razonablemente continua entre variables. Euler permitía que las funciones fuesen perfectamente generales, si bien en la práctica las constreñía a las relaciones geométricas y físicas. Fue durante la segunda mitad del siglo XVIII que la definición de función se iría haciendo más general conforme los matemáticos iban descubriendo que muchas curvas o expresiones arbitrarias podían ser objeto de análisis. Alrededor del concepto de función el pensamiento matemático comenzó a disminuir su dependencia de las intuiciones geométricas y físicas. […]
Calculando con los números escritos “a la Cauchy” — Cuaderno de Cultura Científica
[…] Para saber más:De la grandeur a las matemáticas puras […]
la monstruosa función de Weierstrass
[…] o para estudiar el comportamiento de las corrientes eléctricas. Pero, para el siglo XIX, los matemáticos alemanes comenzaron a desmantelar cosas. Se propusieron encontrar contraejemplos que socavaran suposiciones […]