El pasado mes de diciembre (de 2012) se concedió el Premio Euskadi de Literatura 2012, en castellano, a la excelente novela Tangram, del escritor bilbaíno Juan Carlos Márquez. Rápidamente llamó mi atención el título de la novela, que hacía referencia a un puzzle geométrico de origen chino muy popular dentro de la comunidad matemática, y no había pasado ni un día cuando me pasé por una librería de la ciudad en la que vivo, Bilbao, para comprármela y un par de días después ya había terminado su lectura.

Tangram es una novela que está magníficamente escrita, de fácil lectura, seguramente por el saber hacer de su autor, su dominio del monólogo interior, de los diálogos y de la narración, y que engancha al lector hasta la última página. Está formada por siete historias cortas, cada una de las cuales se podrían leer de forma independiente, pero que puestas juntas conforman también una historia, como ocurre con el puzzle geométrico tangram, que está formado por siete piezas que puestas juntas forman una figura, inicialmente un cuadrado… así el puzzle geométrico se convierte en una metáfora de la interesante estructura de esta obra que nos presenta Juan Carlos Márquez.

El tangram es un juego de origen chino, que según algunos autores podría existir desde la antigüedad (por ejemplo, los griegos ya jugaban con puzzles geométricos similares, así Arquímedes escribe sobre el Stomachion en algunos de sus textos, en el siglo III a.c.). Y al igual que ocurre con otros juegos existe una leyenda fantástica sobre su origen. En ella un emperador chino mandó que fabricaran para él una hoja de vidrio cuadrada de grandes dimensiones. Durante el transporte de la misma, se cayó y se rompió en siete pedazos, y al intentar reconstruir la pieza original, los sirvientes comprobaron que se podían unir de muchas maneras distintas, componiendo no solo el cuadrado original, sino también gran cantidad de figuras geométricas o de objetos cotidianos. Maravillados ante las posibilidades de las siete piezas en las que se había roto el cuadrado de vidrio inicial, siguieron su camino hasta palacio y allí presentaron al emperador las siete piezas que formaban el cuadrado de vidrio, así como algunas de las configuraciones que se podían crear con ellas. En la leyenda, el emperador quedó maravillado con el juego, por suerte para los sirvientes, para los cuales peligraba su vida.

Según algunos autores –como por ejemplo Robert J. Sternberg- su origen se remonta a la dinastía china Song (que gobernó durante el periodo 960-1279), aunque otros –como Jerry Slocum- creen que el tangram tal como lo conocemos hoy en día pudo ser inventado en China entre 1796 y 1801. La publicación más antigua de la que hay constancia que muestre figuras del tangram, por supuesto de China, es de 1813, aunque las copias que se conservan de la misma son de 1815. Al parecer, el tangram era ya un juego muy popular en China en esa época. En China se conoce con el nombre de Ch’i ch’iao t’u, que significa Siete piezas de la sabiduría. Como anécdota decir que la más extensa enciclopedia sobre el tangram fue escrita en 1858 por una mujer, Ch’ien Yun-Chi, y estaba formada por 6 volúmenes, en los que se proponían 1.700 figuras para construir con las 7 piezas.

Ya a principios del siglo XIX, hacia 1917, el juego se introduciría, con gran éxito, en América y Europa, y rápidamente se empezarían a publicar muchas obras sobre este exitoso rompecabezas chino. Aunque sin lugar a dudas la obra que popularizó el juego fue el libro del creador de puzzles y experto en matemática recreativa, Sam Loyd, titulado El octavo libro de Tan (1903). Este contenía otra historia fantástica sobre su origen, fruto de le mente creativa de Sam Loyd. Según el libro, el juego fue inventado hace 4.000 años por el dios Tan, y fue descrito en los siete primeros libros de Tan, cada uno de los cuales contenía 1.000 figuras o diagramas (Tan-grams) que se suponía que ilustraban la creación del mundo y el origen de las plantas y animales. También relacionaba las siete piezas del puzzle con los 7 “planetas” (cuerpos visibles en el cielo) de la antigüedad, la Luna, Marte, Mercurio, Júpiter, Venus, Saturno y el Sol. Sam Loyd propuso 652 figuras en su libro, algunas cuyo origen estaba en las publicaciones chinas y otras inventadas por él.

Existen diferentes versiones sobre el origen del término “tangram”. Una de las más aceptadas es que la palabra proviene de la unión del vocablo cantonés “tang”, que significa “chino” (aunque en la wikipedia puede leerse que quizás haga referencia a la dinastía china Tang), y el vocablo latino «gram» que significa escrito o gráfico. Según otra versión, el término “tangram” se relaciona con la gente que vivía a orillas del río Tanka, en China, los cuales eran grandes comerciantes y además estaban relacionados con el comercio del opio. Y los navegantes occidentales habrían conocido el juego al llegar a sus puertos.

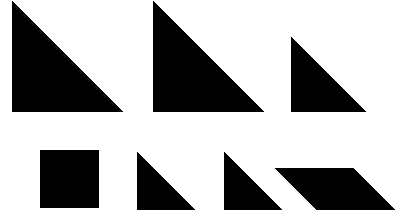
Pero vayamos al puzzle en sí mismo y a las reglas del juego. Para empezar, como ya hemos dicho, este puzzle está formado por 7 piezas, llamadas tans, con las que se puede formar un cuadrado, que suele ser la configuración inicial. Las piezas son las siguientes:

• 5 triángulos de diferentes tamaños (dos grandes, uno mediano y dos pequeños)
• 1 cuadrado
• 1 paralelogramo romboide

Además, estas figuras tienen las siguientes propiedades físicas, como puede verse en la imagen anterior. El triángulo grande tiene el doble de área que el triángulo mediano, y este el doble de área que el triángulo pequeño, y la misma que el cuadrado y el paralelogramo. O podríamos especificar más sobre las medidas de los lados. Así, el cateto del triángulo grande es igual a la hipotenusa del triángulo mediano, el cateto del triángulo mediano es igual a la hipotenusa del triángulo pequeño, a la diagonal del cuadrado o al lado mayor del paralelogramo, y el cateto del triángulo pequeño es igual al lado del cuadrado y al lado menor del paralelogramo. Y los ángulos de las figuras son claramente de 90º, 45º o 135º (90+45).

Las reglas clásicas del Tangram son muy sencillas: se trata de colocar las piezas del puzzle para obtener distintas configuraciones geométricas, letras, siluetas de animales, plantas, personas,… además de esa configuración inicial que es el cuadrado. En principio en cada figura se han de utilizar las siete piezas, todas ellas han de descansar sobre un mismo plano y no se pueden superponer, además se tienen que tocar entre sí. Con estas reglas tan sencillas se pueden construir tantas figuras como nuestra imaginación nos permita. Algunas de ellas serían… cisnes, gatos, osos, patos, aves, conejos, gallinas, perros, peces, buitres, y muchos otros animales. También personas en diferentes posiciones, caras de personas, letras y números, figuras geométricas, y un largo etcétera… el límite es la imaginación de las personas que juegan con este puzzle.

Hoy en día el Tangram no sólo se usa como un entretenimiento, se utiliza también en psicología, en educación física, en diseño, etc.

En el área de enseñanza de las matemáticas el Tangram se utiliza para introducir conceptos de geometría (ángulos, perpendicularidad, paralelismo, teorema de Pitágoras, raíz de dos, área y perímetro de polígonos, fracciones,…) y para promover el desarrollo de capacidades psicomotrices e intelectuales de las personas, pues permite ligar de manera lúdica la manipulación concreta de materiales con la formación y consolidación de ideas abstractas.

Por ejemplo, uno de los problemas con los que se han divertido los matemáticos ha sido la construcción de las posibles figuras convexas (una figura es convexa, si para cualesquiera dos puntos de la misma, el segmento que los une sigue estando dentro de la figura, como ocurre con el cuadrado original o con un triángulo rectángulo que también se puede construir con las 7 figuras básicas). En 1942 dos matemáticos chinos, Fu Tsiang Wang y Chuan-Chih Hsiung, demostraron que se pueden construir exactamente 13 figuras convexas. Dejamos para los lectores y lectoras de este artículo el placer de intentar redescubrir los 13 diseños.

Pero volvamos a la novela de Juan Carlos Márquez… la cual, como ya se ha mencionado, está formada por siete historias, que están marcadas en el libro con un tan, una pieza del Tangram, y un título. Por ejemplo, la primera es el cuadrado y se titula “El sótano”, o la última es el paralelogramo (romboide) y se titula “Gemelas”. Cada historia es a priori independiente, su lectura no depende de la lectura de las demás e incluso cada historia está narrada desde el monólogo interior de un personaje diferente. Pero además, puestas juntas forman una historia común. Buscando la analogía con el tangram, sería algo así como si esa historia común, la que cuenta la novela, se hubiese roto en diferentes piezas más pequeñas, cada una con una entidad propia.

Mientras que las historias inicial y final se identifican con el cuadrado y el paralelogramo, las cinco historias intermedias se identifican con los triángulos, pero no se especifica qué triángulo es cada una de ellas. Y yo me pregunto… ¿el autor de esta novela, mientras la escribía, tenía identificada cada historia con una pieza real? ¿las tenía asignadas inicialmente o a posteriori? ¿nos plantea acaso el juego de que las identifiquemos nosotros? ¿cómo pegan unas piezas con otras?… ¿o la relación con el tangram es más bien metafórica?

Como hemos comentado cada historia está narrada desde el monólogo interior de un personaje distinto, además cada historia tiene sus propios personajes, así como su espacio y su tiempo particulares. Algunos personajes aparecen en varias historias, pero muchos otros no, solo forman parte de una sola historia. Así el policía Basilio Olabarrieta, que aparece al final de la primera historia (El sotano-cuadrado), es el personaje central de la siguiente (El caso Iabichino-triángulo), o Norberto Fraile que es uno de los jóvenes que es encerrado en el sótano de la primera historia, es el personaje central de La Liga de la sinceridad-triángulo y aparece mencionado también en la última historia, gemelas-paralelogramo, mientras que la mayoría de los personajes de la historia Crotona-triángulo, en la que aparece por primera vez en el tiempo lineal, que no en una historia, un personaje central en la novela como es el actor Gaetano Iabichino, no vuelven a aparecer en ninguna otra historia. Yo, en una primera lectura, he jugado a intentar ver si podría asignar a cada historia una pieza real del tangram de manera que piezas que comparten un lado común (en la solución cuadrada del tangram) tengan también, al menos un personaje en común… y sí ha sido posible.

Me gustaría terminar con un par de cuestiones menores relacionadas también con las matemáticas, que aparecen en la novela Tangram…

a) En la quinta historia, Un millón de libras-triángulo, se hace una ligera referencia a lo que es un sistema cartesiano de coordenadas…

“El dinero está encerrado al Noreste de un prado, a ciento setenta y cuatro pies (ciento cinco al frente y sesenta y nueve a la derecha) de un poste eléctrico en el borde de un camino polvoriento, pero en cuanto me apeo del coche…”

Para determinar la posición de un punto en el plano se necesitan dos números, que en la novela son “ciento cinco”y“sesenta y nueve”,pero por sí solos no nos sirven de mucho, necesitamos además un punto destacado (el origen), que en nuestro caso es “un poste eléctrico”y dos rectas perpendiculares que se cortan en el origen (respecto de las cuales se miden las distancias), que los matemáticos dibujamos en nuestro plano cartesiano ideal, pero que en la novela están indicados por la carretera (que sería la dirección derecha/izquierda) y su perpendicular, que es la dirección a la que se refiere el protagonista cuando habla de “ciento cinco [pasos] al frente”. Un ejemplo cotidiano de sistema de referencia sería el siguiente. Cuando estamos en una habitación de nuestra casa, tomamos una esquina como referencia y los dos números que determinan la posición de la habitación que nos interesa están dados por las distancias de esa posición a cada una de las paredes, que son los ejes coordenados.

b) la otra cita matemática de la novela es sobre el matemático más conocido, Pitágoras… y aparece mencionado en la sexta historia, Crotona-triángulo.

“Dicen que muy cerca, o quizá sobre esa misma tierra reseca y agrietada, Pitágoras edificó hace más de dos mil años su escuela de Matemáticas. Uno de sus discípulos, Milón de Crotona (todo un héroe local) destacó en la lucha y venció en varios Juegos Olímpicos, y a él se le atribuyen hazañas inverosímiles, tales como conseguir detener un carro lanzado a toda velocidad o cargar un toro sobre sus hombros. La señorita Maldovani es romana y, cuando se enoja, acostumbra a decir tras un largo respingo que en sus aulas año tras año la historia de Crotona se repite: que faltan pitágoras y sobran milones”.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica