En la entrada del Cuaderno de Cultura Científica titulada El arte contemporáneo mira al Tangram estuvimos viendo como algunos artistas contemporáneos utilizaban el Tangram como un elemento fundamental en el desarrollo de algunas de sus obras de arte.
En particular, pudimos observar que, entre las configuraciones posibles con las siete piezas de este rompecabezas geométrico, un grupo que llamaba especialmente la atención de estos artistas era la familia de configuraciones convexas, quizás por ser una familia muy matemática. En la entrada de hoy vamos a hablar precisamente de este tipo de configuraciones, en qué consisten y cuántas existen.

Puesto que esta entrada va a ser algo más matemática, volvamos a introducir y observar, desde una óptica más geométrica, el rompecabezas Tangram y las siete piezas poligonales que lo componen.
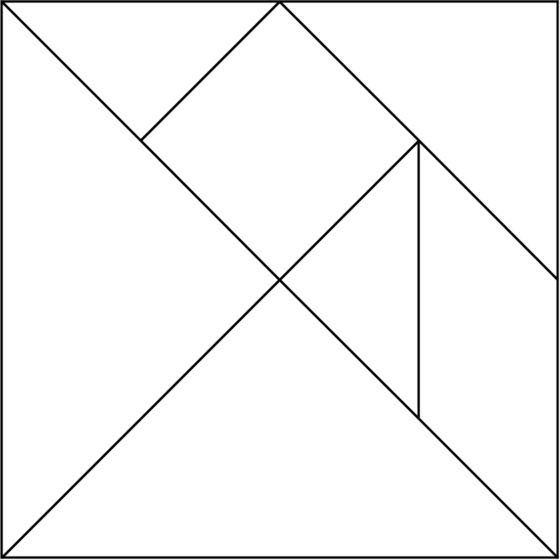
Para empezar, volvamos a observar las siete piezas poligonales que forman el Tangram, dos triángulos pequeños, un triángulo mediano y dos triángulos grandes, todos ellos con la misma forma –triángulo rectángulo isósceles–, pero distintos tamaños (sus ángulos son 90, 45 y 45 grados), un cuadrado (con cuatro ángulos de 90 grados) y un romboide (cuyos ángulos son 45, 135, 45 y 135 grados, pero observemos que 135 = 90 + 45). Todas las piezas son “simétricas”, en el sentido de que si se voltean no cambian de forma, son la misma figura (tienen simetría especular), salvo el romboide, que si se voltea cambia su orientación. Por lo tanto, el romboide tiene dos posibilidades a la hora de ser utilizado para realizar una configuración, como la original del cuadrado.
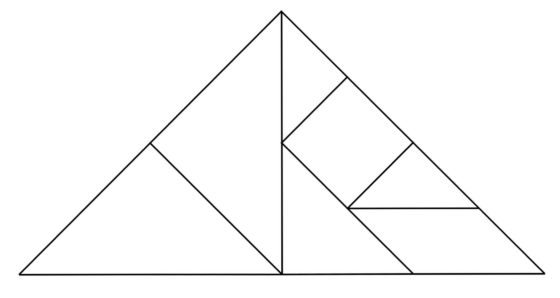
Una cuestión interesante de las piezas del Tangram, que además va a ser fundamental en el estudio de las configuraciones convexas, es que las piezas del Tangram pueden ser divididas en triángulos rectángulos isósceles, del mismo tamaño que las dos piezas triangulares pequeñas del Tangram, como se muestra en la siguiente imagen. De esta forma, las piezas del Tangram pueden dividirse en 16 triángulos rectángulos isósceles iguales.
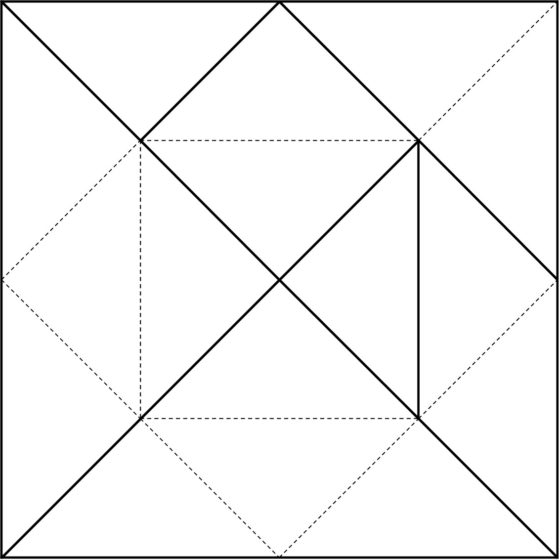
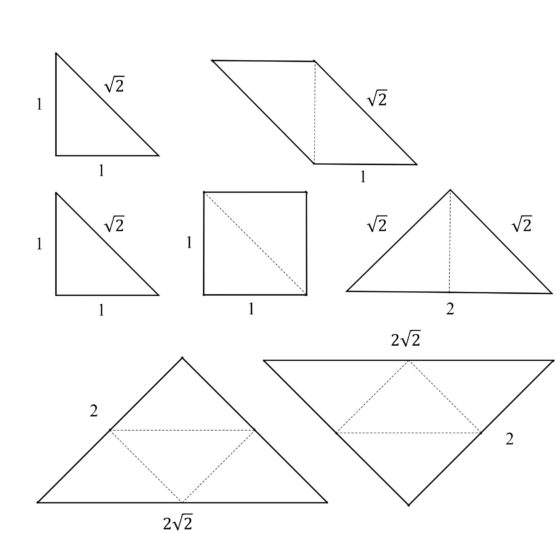
Si consideramos que los dos lados iguales de estos triángulos rectángulos isósceles, que son los catetos, miden 1 (son nuestra unidad de medida), entonces la hipotenusa medirá, por el teorema de Pitágoras, raíz de 2. Es decir, bajo esta premisa podemos considerar que dos lados del triángulo rectángulo isósceles son “lados racionales” y el otro es un “lado irracional”.
Además, teniendo en cuenta esto podemos ver, en la siguiente imagen, las medidas de las piezas del Tangram. Así mismo, podemos calcular sus áreas. El área de los triángulos pequeños es 0,5, el área del cuadrado, el triángulo mediano y el romboide es 1, y el área de los triángulos grandes es 2.
El objetivo del rompecabezas geométrico es buscar la forma de colocar las piezas para obtener una configuración dada del mismo, como el cuadrado básico, pero también otras configuraciones, ya sean figurativas (personas, animales, árboles, flores, edificios, letras, números, etc) o geométricas (polígonos convexos, estrellas, poliominós, etc), o incluso diseñar nuevas configuraciones. Puede ocurrir que una configuración dada no tenga ninguna solución, en cuyo caso hay que buscar la forma de demostrar que no la tiene, o en caso de tener solución puede analizarse cuántas formas distintas de conseguir esa configuración existen.
Por ejemplo, si tomamos la configuración básica del Tangram solo existe una solución de la misma, salvo rotaciones y reflexiones (dar la vuelta), que se extendería a 8 soluciones si admitiésemos como distintas las rotaciones y reflexiones (dar la vuelta), como se muestra en la siguiente imagen.

El gran divulgador de las matemáticas Martin Gardner (1914-2010), en su primer artículo sobre el Tangram de su columna Mathematical Games de la revista Scientific American, titulado On the fanciful history and the creative challenges of the puzzle game of tangrams, mostraba una colección de configuraciones con el reto de obtenerlas con las siete piezas, pero una de ellas no era posible y la cuestión era, además, demostrar por qué no era posible. A continuación, mostramos estas configuraciones.
Reto: Obtener estas configuraciones con las siete piezas del Tangram y demostrar que una de ellas es imposible (la demostración al final de la entrada).

Desde el punto de vista matemático, los problemas más interesantes son los de tipo combinatorio. Cuestiones como las siguientes: ¿cuántos polígonos convexos pueden formarse con las piezas del Tangram?, ¿cuántos polígonos de tres, cuatro o cinco lados pueden construirse?, ¿cuántos poliominós (donde un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados, como vimos en la entrada Embaldosando con L-triominós (un ejemplo de demostración por inducción)?, ¿cuántas formas estrelladas pueden formarse?, etc.
Antes de continuar, recordemos que un polígono convexo es un polígono cuyos ángulos interiores miden menos de 180º, es decir, no hay zonas que externas metidas hacia dentro. En general, en matemáticas, se dice que un conjunto es convexo, si dados dos puntos cualesquiera del conjunto se verifica que los puntos del segmento que une esos dos puntos está también dentro del conjunto.
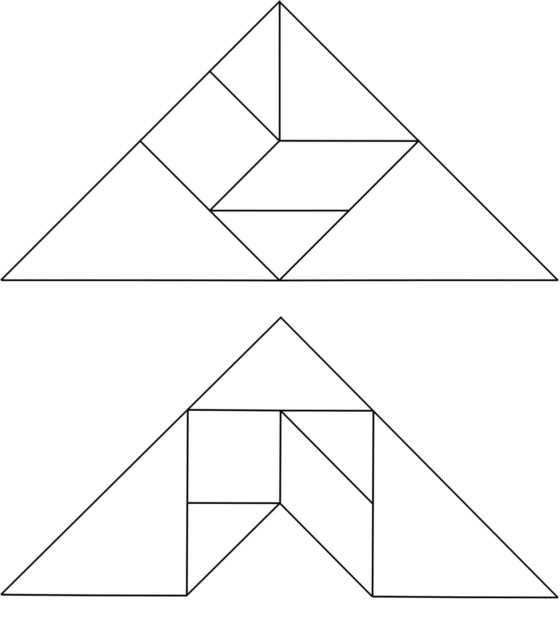
Antes de entrar en el teorema sobre el Tangram referido al número de configuraciones convexas que existen, primero pensemos cuántos triángulos, polígonos de tres lados, se pueden construir con las piezas del Tangram. La respuesta es sencilla, únicamente el triángulo de la imagen anterior, que es un triángulo rectángulo isósceles (con ángulos de 45, 45 y 90 grados). El motivo es que los ángulos de las piezas del Tangram son 45, 90 y 135 grados, como la suma de los ángulos de un triángulo es 180 grados, la única opción posible es 45, 45 y 90 grados, es decir, el triángulo rectángulo anterior.
Observemos ahora que la solución anterior de la configuración triangular del Tangram no es la única, en contraposición a lo que ocurría con el cuadrado básico. Por ejemplo, otra posible solución es la que mostramos a continuación.
Si nos planteáramos qué ocurre con las figuras cuadriláteras, si es posible que existan figuras no convexas de cuatro lados, la respuesta es negativa. La única opción posible para los cuatro ángulos es tres ángulos de 45 grados y uno de 225 grados, el problema es que no se puede realizar esta figura con 16 triángulos rectángulos isósceles del tamaño de las piezas triangulares pequeñas del Tangram. Luego todos los cuadriláteros que se puedan construir serán convexos.
Pero vayamos al resultado importante respecto a las configuraciones convexas del Tangram, la existencia únicamente de 13 polígonos convexos realizados con las figuras del rompecabezas.
Teorema (F.T. Wang, Ch. Hsiung, 1942): Utilizando las piezas del Tangram se pueden formar exactamente trece polígonos convexos.
Los matemáticos chinos Fu Traing Wang y Chuan-Chih Hsiung, en su artículo publicado en The American Mathematical Monthly en 1942, demostraron primero algunos lemas (resultados técnicos previos) que tenían en cuenta fundamentalmente el carácter racional e irracional de los lados de los dieciséis triángulos rectángulos isósceles y que nos permiten entender mejor la situación, así como simplificar la demostración del resultado matemático.
Lema 1. El primer lema dice que, si utilizamos dieciséis triángulos rectángulos iguales para formar un polígono convexo, entonces un lado racional de un triángulo no puede apoyarse en un lado irracional de otro triángulo, como en la imagen siguiente.
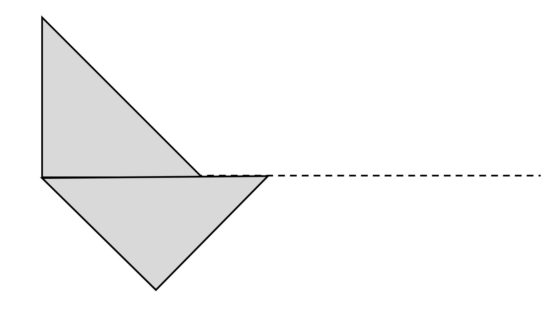
Si nos fijamos en la imagen de arriba, los dos triángulos apoyados uno en otro, racional frente a irracional, la figura es claramente no convexa con solo esas dos piezas. Si dibujamos la recta que extiende el lado compartido de los triángulos, podemos observar que:
1. No hay forma de que ninguna pieza atraviese esa línea;
2. Si en la parte superior colocamos triángulos con el lado racional apoyado en la recta, como el que está, y en la parte inferior colocamos triángulos con el lado irracional apoyado en la recta, no hay forma de que coincidan los vértices sobre la recta, ya que una cantidad racional, la suma de los lados de arriba, no puede ser igual a una cantidad irracional, la suma de los de abajo, por lo que siempre quedará una situación no convexa, similar a la de la imagen;
3. La única forma de igualar las longitudes de las piezas que se apoyan en la parte superior e inferior de la recta, es apoyando desde arriba un triángulo con su lado irracional y desde abajo un triángulo con el racional, como se muestra en la imagen.

Pero, en este caso, para romper la no convexidad de la figura formada hay que incluir más triángulos en las zonas con una estrella, lo que nos lleva a volver a poner necesariamente otro lado irracional sobre uno racional y volver a la misma situación inicial, luego de no convexidad.
Lema 2. Si se tiene en cuenta el primer lema, en particular, el argumento del punto 3, se tiene que, si utilizamos dieciséis triángulos rectángulos iguales para formar un polígono convexo, entonces los lados del polígono están formados por lados del mismo tipo (racionales o irracionales) de los triángulos. Además, se dice que un lado del polígono convexo es racional, o irracional, cuando está formado por lados racionales, o irracionales (respectivamente), de los triángulos. En general, los lados racionales e irracionales del polígono convexo alternan, pero si un ángulo del polígono es recto, los lados adyacentes son ambos racionales o irracionales.
Si miramos a la solución del Tangram con forma triangular, pero vista como formada por los dieciséis triángulos rectángulos isósceles del mismo tamaño, observamos que efectivamente se cumple este lema. Los dos lados adyacentes al ángulo recto son racionales, mientras que el otro, entre ellos, es irracional.
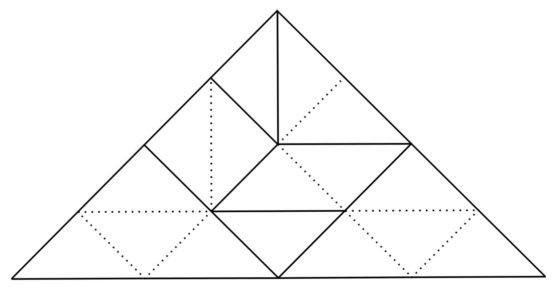
Lema 3. Este lema nos establece un número máximo de lados que puede tener un polígono convexo formado por dieciséis triángulos rectángulos isósceles del mismo tamaño. Por una parte, tiene en cuenta que la suma de los ángulos interiores de un polígono convexo de n lados es (n – 2) x 180 grados (este resultado se puede demostrar fácilmente tomando un punto interior del polígono convexo y dividiendo este en triángulos con uno de sus vértices ese punto interior, con solo tener en cuenta que la suma de los ángulos de un triángulo es 180 grados y que los ángulos alrededor del punto interior suman 360 grados) y, por otra parte, que en cada uno de los n vértices del polígono convexo la suma máxima que pueden alcanzar los ángulos que proporcionan los triángulos es 135 grados. Considerando ambas informaciones se tiene que la suma de los ángulos interiores del polígono convexo, (n – 2) x 180 grados, es menor o igual que n x 135 grados, de donde, n es menor o igual que 8.
En conclusión, no hay polígonos convexos de más de 8 lados que puedan ser formados con 16 triángulos rectángulos isósceles iguales.
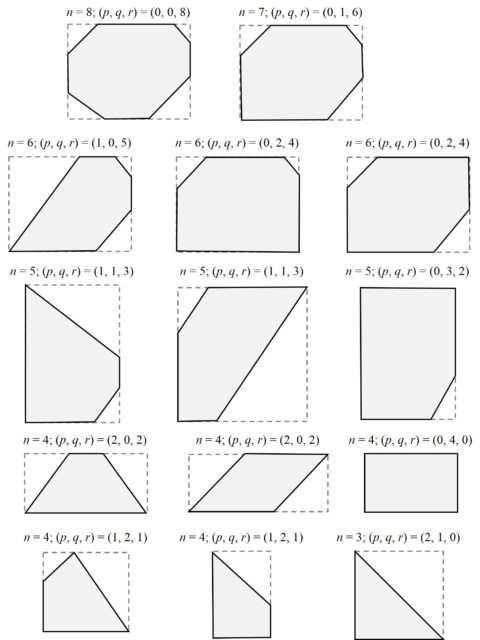
Lema 4. Teniendo en cuenta los lemas anteriores y que los ángulos del polígono convexo solo pueden tener los valores 45, 90 y 135 grados, se obtiene que, si utilizamos dieciséis triángulos rectángulos iguales para formar un polígono convexo, entonces este polígono está inscrito en un rectángulo con todos los lados racionales, o irracionales, del polígono apoyados en los lados del rectángulo.
Si consideramos que el polígono convexo tiene p ángulos de 45 grados, q de 90 grados y r de 135 grados, y que la suma de los ángulos del polígono convexo es (n – 2) x 180 grados, se tiene que 2p + q = 8 – n, luego como el polígono tiene como mucho 8 lados, entonces se tienen las siguientes posibilidades para los valores de (p, q, r):
Con los anteriores resultados, ya estamos en condiciones de demostrar este teorema sobre el Tangram.
Demostración del teorema. Para empezar, podemos asumir que el polígono convexo generado con los dieciséis triángulos rectángulos isósceles iguales es un octógono, que denotamos de la siguiente forma ABCDEFGH (sus vértices), ya que podemos considerar que los polígonos con menos lados son octógonos degenerados, en los que algunos lados tienen longitud cero, es decir, son solo vértices. Por otra parte, podemos suponer que el polígono está inscrito en un rectángulo PQRS tal que los lados racionales del polígono BC, DE, FG y HA son los que se apoyan en los lados del rectángulo.
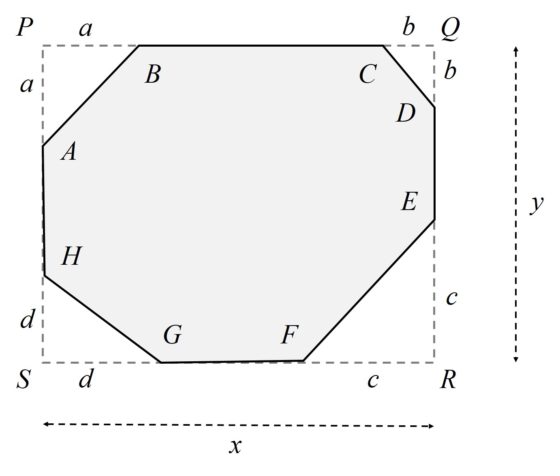
A continuación, llamamos a, b, c y d al número de lados irracionales de los triángulos rectángulos isósceles que forman los lados irracionales del octógono AB, CD, EF y GH, respectivamente. Si seguimos con la convención de que los lados racionales de los dieciséis triángulos rectángulos isósceles iguales miden 1 (por el teorema de Pitágoras, los irracionales miden raíz de 2), entonces resulta que los números naturales a, b, c y d (que podrían valer 0 en el caso de un octógono degenerado) son las longitudes de los catetos de los triángulos rectángulos APB, CQD, ERF y GSH, cuyas hipotenusas son los lados irracionales del octógono, como puede observarse en la anterior imagen. El siguiente diagrama nos muestra la justificación de lo anterior.
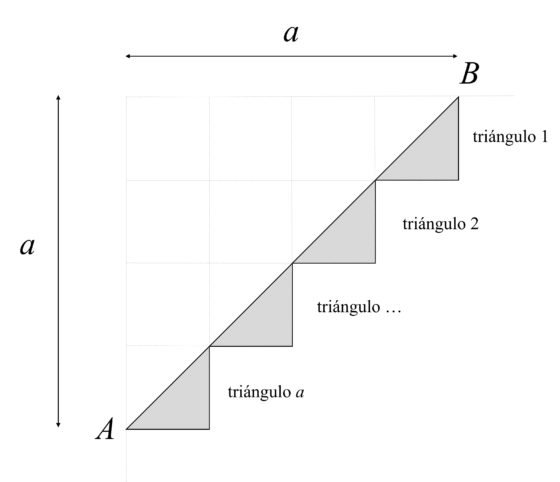
Y llamamos x e y a las longitudes de los lados del rectángulo en el que está inscrito el octógono, como se indica en la imagen de más arriba. Ahora, por un simple razonamiento de áreas en el diagrama del octógono inscrito en el rectángulo, tenemos que los números naturales a, b, c, d, x, y (que pueden tomar también el valor 0) satisfacen la siguiente ecuación:
![]()
con las restricciones naturales siguientes
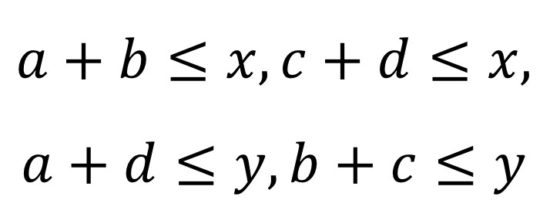
Por lo tanto, hemos reducido la demostración del resultado sobre las configuraciones convexas del Tangram a la búsqueda de soluciones enteras (no negativas) de la anterior ecuación, con sus restricciones y de las mismas (ya que estas se corresponden a disposiciones con los 16 triángulos rectángulos isósceles iguales) determinar cuáles son posibles mediante las piezas del Tangram.
En esta entrada nos vamos a saltar la parte de la demostración que consiste en buscar las soluciones enteras, no negativas, de la anterior ecuación. Para las personas que estén interesadas les remitimos al artículo original A theorem on the Tangram, de Wang y Hsiung, o al artículo Finding all convex tangrams, de T.G.J. Beelen, que se incluyen en la bibliografía. A continuación, mostramos una tabla con las soluciones para las incógnitas a, b, c, d, x, y, además, están marcadas con un asterisco aquellas que no se corresponden con configuraciones del Tangram.

De donde podemos construir los trece poliedros convexos posibles con las siete piezas del Tangram.
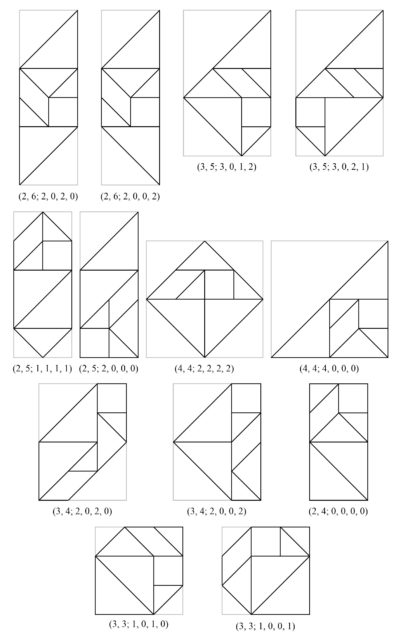
Por otra parte, las siete construcciones posibles con dieciséis triángulos rectángulos isósceles iguales, pero que no son realizables con las piezas del Tangram son las siguientes.

Vamos a terminar con un grabado basado en una de las trece construcciones poligonales convexas del Tangram, realizada por el artista italiano Francesco Moretti, de quien ya hablamos en la anterior entrada El arte contemporáneo que mira al Tangram.

Pero no hemos terminado del todo, aún nos queda la solución del reto que habíamos planteado.
Solución del reto: Para terminar, resolvamos la parte del reto de la configuración que es imposible de realizar. Esta es el cuadrado con un agujero cuadrado en el centro. Demostremos que no es posible realizarla con las siete piezas del Tangram. Si observamos bien la configuración, vemos que efectivamente la superficie de la misma está formada por 8 cuadrados, es decir, 16 triángulos rectángulos isósceles, como las 7 piezas del Tangram. Si vemos donde pueden ir colocadas las piezas triangulares grandes, resulta que solo pueden ir colocadas en dos esquinas opuestas de la configuración, como se muestra en la imagen de abajo. Además, la pieza cuadrada solo podrá ir en una de las dos esquinas libres.
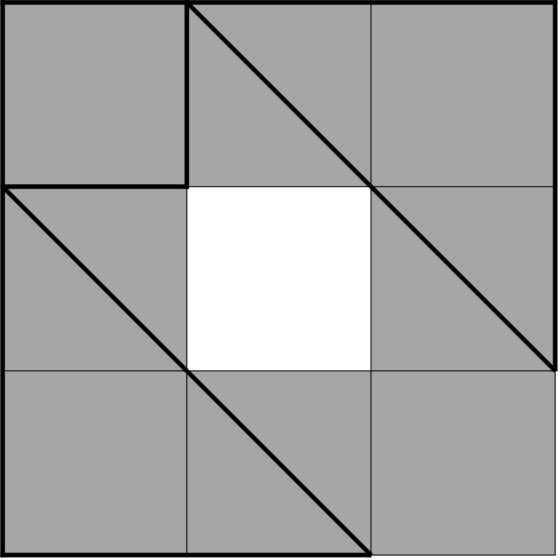
El problema es que la pieza romboide solo puede ir pegada a la única esquina que queda libre, pero entonces no hay sitio para poder colocar la pieza triangular mediana. En conclusión, es imposible realizar esta configuración.
Bibliografía
1.- Fu Traing Wang, Chuan-Chih Hsiung, A theorem on the Tangram, The American Mathematical Monthly, vol. 49, no. 9, pp. 596-599, 1942.
2.- Martin Gardner, Viajes en el tiempo y otras perplejidades matemáticas, RBA, 2010 (los dos artículos originales de Martin Gardner sobre el Tangram que aparecen en este libro fueron publicados originalmente en la columna Mathematical Games de la revista Scientific American en 1974)
3.- Paul Scott, Convex Tangrams
4.- T.G.J. Beelen, Finding all convex tangrams, CASA-report Vol. 1702, Technische Universiteit Eindhoven, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Ernesto Arellano González
Todas las demostraciones de diferentes teoremas me agradan y más cuando lo logro por mi mismo, ahora que presentan estas diferentes formas de usar Geometría más me agradan las matemáticas, lo malo que ya soy un poco grande de edad, pero no dejaré de seguir sus pasos y dejando semillas sembradas en mis estudiantes que no dejen nunca de estudiar. Gracias por compartir sus conocimientos.
Rosario Pérez
Muy enriquecedora e interesante aportación del Tangram
Un teorema sobre el Tangram | tangram | Scoop.it
[…] En la entrada del Cuaderno de Cultura Científica titulada El arte contemporáneo mira al Tangram estuvimos viendo como algunos artistas contemporáneos utilizaban el Tangram como un elemento fundamental en el desarrollo de algunas de sus obras de arte.En particular, pudimos observar que, entre las configuraciones posibles con las siete piezas de este rompecabezas geométrico, un grupo que llamaba especialmente la atención de estos artistas era la familia de configuraciones convexas, quizás por ser una familia muy matemática. En la entrada de hoy vamos a hablar precisamente de este tipo de configuraciones, en qué consisten y cuántas existen. […]