Trigonometría para piratas
El escarabajo de oro (1843) es un cuento de piratas escrito por el genial Edgar Allan Poe. El protagonista, William Legrand, encuentra un pergamino que contiene un criptograma que conduce al tesoro escondido por el pirata Kidd.
Pero no quiero hablar de la criptografía de El escarabajo de oro, sino de un problema de trigonometría relacionado con el cuento. Para ello, es necesario repasar un poco el argumento y ciertas medidas de las que Poe habla.
El mensaje escondido por el pirata, una vez traducido por Legrand, dice:
Un buen vaso en la hostería del obispo en la silla del diablo cuarenta y un grados y trece minutos nordeste cuatro de norte, principal rama séptimo vástago lado este solar desde el ojo izquierdo de la cabeza de muerto una línea recta desde el árbol a través de la bala cincuenta pies fuera.
Tras realizar diferentes investigaciones, Legrand descubre el lugar al que alude el mensaje. Obliga a su esclavo Júpiter a trepar a un tulipero hasta que llega a la séptima rama, al final de la cual encuentra una calavera clavada –la cabeza de muerto– y desde el ojo izquierdo suelta un objeto pesado –el escarabajo de oro–. En el lugar en el que cae, Legrand marca con ayuda de una estaca un punto de referencia, y en la dirección señalada por el tronco y la estaca recorre una distancia de 50 pies. ¡El tesoro tiene que estar allí debajo! Comienzan a cavar, trazando para ello un círculo de 4 pies de diámetro. Tras dos horas trabajando, no encuentran nada. El pobre Júpiter ha confundido la derecha con la izquierda, así que Legrand desplaza la estaca unas 2,5 pulgadas hacia el oeste –lo que estima que distan las dos órbitas de los ojos de la calavera–, y con este nuevo punto de referencia recorre 50 pies, vuelve a marcar un círculo un poco mayor que el primero y allí comienzan a cavar. Esta vez encuentran el tesoro. Os recomiendo que leáis la historia completa… es deliciosa.
El matemático Erik Talvila (University of Alberta, Canadá) sostiene en su artículo Trigonometry of the Gold-Bug [footnote]Erik Talvila, Trigonometry of the Gold-Bug, Mathematical Gazette 97, no. 538, 124-127, 2013. Puede verse el artículo en el repositorio arXiv: http://arxiv.org/pdf/1206.1761v1.pdf[/footnote], que mediante un simple argumento trigonométrico se comprueba que, de hecho, los dos hoyos excavados por Legrand y sus amigos se superponen parcialmente.
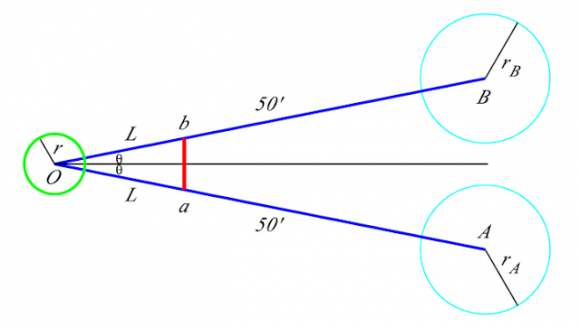
Talvila se basa en la siguiente figura que resume la situación anteriormente descrita:
Los puntos indicados en la figura son el centro del árbol O, el punto en el que cae el escarabajo de oro a través del ojo derecho de la calavera a, el punto en el que debería haber caído el escarabajo de oro a través del ojo izquierdo b, el primer hoyo A y el segundo B. Las distancias indicadas son el radio del tronco del árbol r, la distancia de cada ojo del cráneo al tronco de tulipero L, el radio del primer hoyo rA, y el radio del segundo rB. Las distancias se dan en pies –un pie equivale a 30,48 cm o a 12 pulgadas–. El ángulo AOB es de 2θ.
Como ya hemos comentado, los puntos a y b distan 2,5 pulgadas, es decir, 5/24 pies. La distancia entre a y A (y entre b y B) es de 50 pies, y el seno del ángulo θ es:
La distancia entre los centros de cada uno de los hoyos es entonces:
Para que los dos agujeros no se solapen, debe ser AB > rA + rB; reordenando los términos de esta inecuación, queda:
Según el cuento, rA mide 2 pies. Se dice que rB es un poco más grande, pero pongamos por simplificar que también mide 2 pies. Así, para que los dos hoyos cavados no se superpongan, debe ser
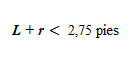
¿Es esto posible? Talvila comenta en el artículo que un tulipero de su campus –no especialmente viejo– mide unas 25 pulgadas de diámetro, es decir, unos 2,1 pies. Es decir, suponiendo que r = 1 pie, debería ser:
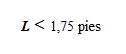
Pero, según describe Poe, Júpiter debe deslizarse hasta el final de la séptima rama para acceder a la calavera… seguro que recorre más de 3 pies –es decir, L > 3 pies– para alcanzarla. ¡Así que los hoyos deben superponerse parcialmente!
¡Poe –que seguro que sabía trigonometría– debería haber repasado sus cuentas!
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

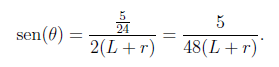
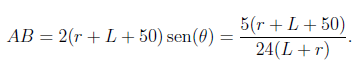
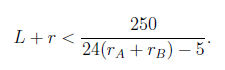
Trigonometría para piratas
[…] Trigonometría para piratas […]
Pitágoras
¡Qué excelente regurgitación!
‘Los bailarines’, un criptograma resuelto por Sherlock Holmes | :: ZTFNews.org
[…] deduciendo, pensando, comparando, etc.–, el detective averigua la clave; se trata –como en El escarabajo de oro de Edgar Allan Poe– de un simple cifrado por sustitución: los bailarines a los que alude el […]
Códigos secretos en la primera guerra mundial | Matemoción | Cuaderno de Cultura Científica
[…] Marta Macho, Trigonometría para piratas, Cuaderno de Cultura Científica, […]
Sherlock Holmes y la criptogafía | Economía Personal
[…] –exactamente de la misma manera en la que procede el protagonista de El escarabajo de oro de Edgar Allan Poe, ver [2]– comienza estudiando la frecuencia de aparición cada símbolo, y la […]
El cifrado de Gronsfeld en “La Jangada” — Cuaderno de Cultura Científica
[…] su defensa, intenta descifrar el contenido del mensaje por diferentes métodos. Jarríquez alude a El escarabajo de oro de Edgard Allan Poe como sistema en el que se basa para intentar encontrar la clave. Pero sus […]