Cualquier persona que viva en una ciudad medianamente grande sabe que la densidad de tráfico y el aparcamiento son dos problemas importantes, y que, en consecuencia, preocupan a su ayuntamiento. Por este motivo, se realizan estudios que analizan, tanto en el conjunto de la ciudad como en cada uno de sus barrios, el parque automovilístico, el uso que los ciudadanos hacen de sus vehículos, el número de plazas para aparcar (en vía pública o en edificios), la oferta de plazas de garaje en venta, los precios de las mismas, las necesidades existentes de nuevas plazas públicas de aparcamiento o la existencia de transporte público que una los diferentes barrios. El objetivo de estos estudios es que los miembros del consistorio tengan un mayor conocimiento de la realidad de su ciudad y tomen las medidas oportunas para dar solución a estos problemas, además el resultado de los estudios suele ser comunicado a los ciudadanos a través de los medios de comunicación.
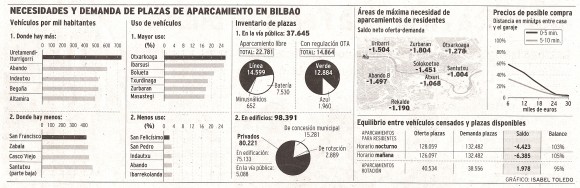
Así, el jueves 5 de marzo de 2009, mientras leía el periódico El Correo, cuya portada y parte de su interior estaba dedicado a la clasificación del Athletic para la final de la copa contra el Barcelona, me encontré con una noticia, a doble página, en la que se analizaban las necesidades y demanda de plazas de aparcamiento en Bilbao. Mis ojos rápidamente, tras leer el titular, se fueron al gráfico que la acompañaba (véase imagen).
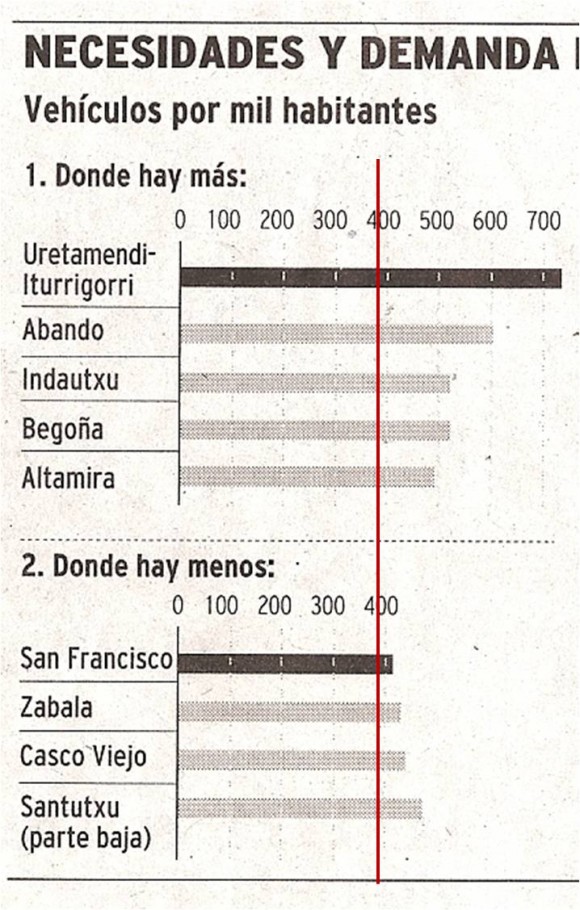
Tras un breve vistazo a la información contenida en el mismo me dispuse a leer el artículo. Nos informaban, por ejemplo, de que “…en Bilbao hay menos coches que en otras ciudades. En concreto 385 por cada mil habitantes, frente a los 415 del País Vasco y los 471 de la media española”. A continuación, se citaban los barrios con mayor, y menor, proporción de vehículos. Y ahí, volví a fijar mi atención en la parte de la noticia en la que se utilizaba un diagrama de barras (horizontales) para indicar la cantidad de coches por cada 1.000 habitantes de dichos barrios (que se muestra a continuación).
Cuál no sería mi sorpresa al comprobar que la proporción de vehículos por cada mil habitantes, tanto de los barrios donde había más coches como en los que había menos (y por lo tanto, de todos los barrios de Bilbao), estaba por encima de esos 385 vehículos por cada mil habitantes, que era la proporción del conjunto de todos los barrios, es decir, de todo Bilbao (en la imagen se ha añadido una barra roja que sitúa la proporción en todo Bilbao, claramente por debajo de las de los barrios).
El sentido común nos dice, como me dijo a mí entonces, que la proporción de vehículos por cada mil habitantes de toda la ciudad (es decir, la unión de todos sus barrios) tenía que estar “por el medio”, es decir, que estaría entre la proporción del barrio con menos vehículos por cada mil habitantes y la del barrio con más vehículos.
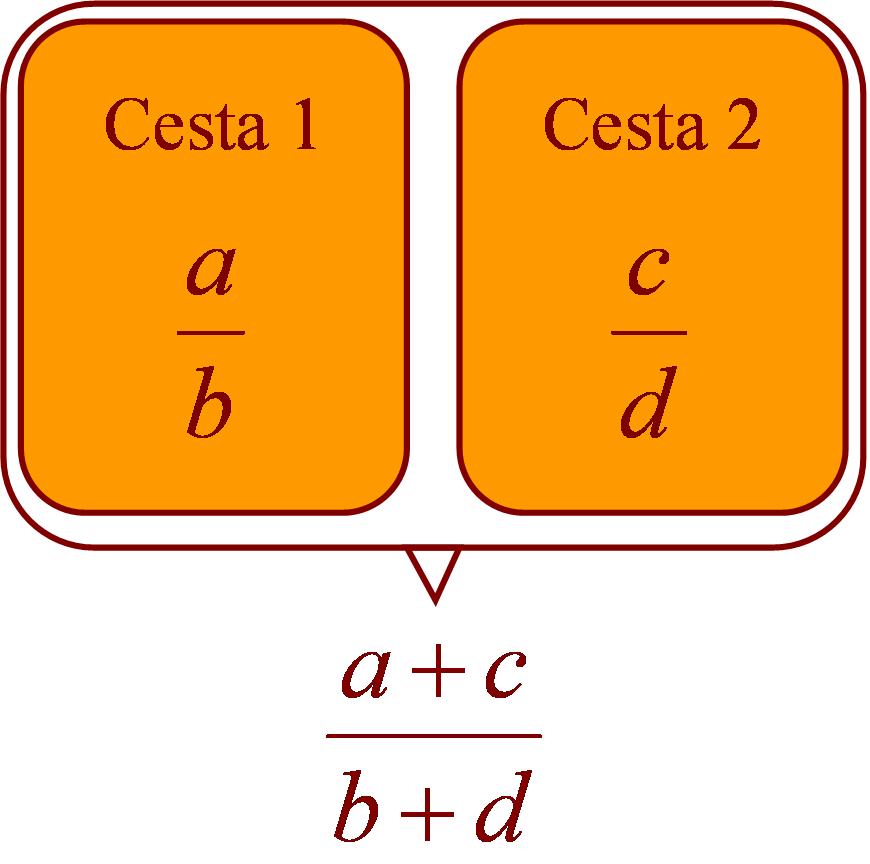
Ilustrémoslo con otro ejemplo. Imaginemos diez agricultores que recogen manzanas de sus huertos para luego venderlas a un mayorista, y que el porcentaje de manzanas rojas (en tantos por cierto) que ha recolectado cada uno de ellos es por ejemplo: 15%, 20%, 17%, 32%, 16%, 28%, 34%, 13%, 24% y 29%. Cuando se juntan todas las manzanas en el almacén del mayorista, el sentido común nos dice que el porcentaje de manzanas rojas dentro del total de manzanas seguro que será mayor que el 13% y menor que el 34%.
Volví a leer la noticia con cuidado y mirar el gráfico de la misma. No había lugar a dudas, parecía haber un error en la información de ese artículo. Pero… a pesar de lo que parecía indicar el sentido común, ¿podría estar yo equivocado? ¿sería posible un efecto similar a la paradoja de Simpson (de la que hablaré en otra ocasión) que va en contra de la intuición? No parecía que fuera el caso, pero para salir de dudas había que ir a las matemáticas que estaban detrás de esta cuestión.
Las matemáticas. Para simplificar el problema podemos pensarlo como si en la noticia hubiese únicamente dos barrios, es decir, únicamente dos proporciones. O si consideramos el ejemplo de las manzanas solo dos agricultores.
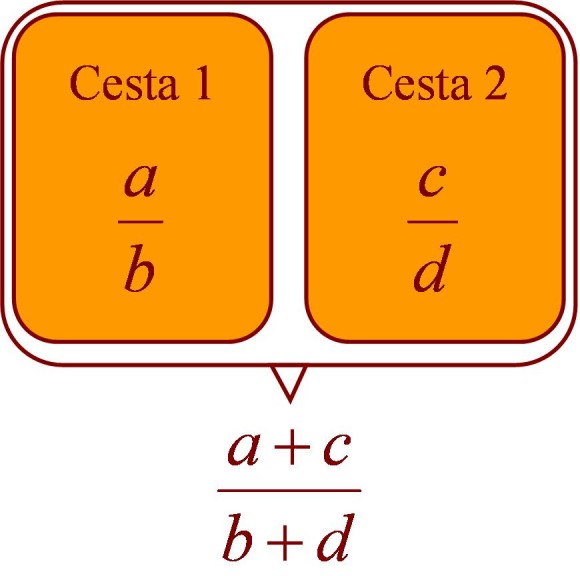
Sea ahora la proporción de manzanas rojas de cada uno de ellos (hay a manzanas rojas de un total de b manzanas) y
(hay c manzanas rojas de un total de d manzanas), respectivamente, entonces la proporción de manzanas rojas en el total de manzanas (uniendo ambas partidas) es
(hay a+c manzanas rojas de un total de b+d). Entonces, lo que parece decirnos la intuición es que la proporción del total debería estar entre la proporción más pequeña y la mayor.
Si ahora nos quedamos únicamente con la parte puramente matemática, el problema sería el siguiente. Dadas dos fracciones y
(siendo a, b, c, d números positivos), tales que
, entonces
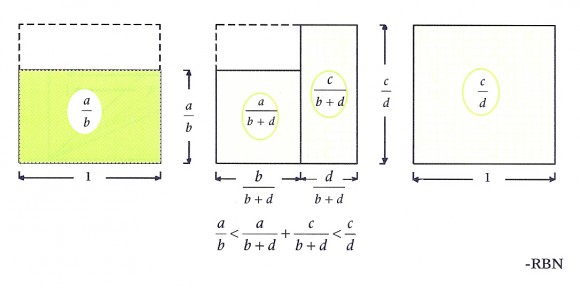
Esta propiedad se conoce como la “Regla de los Nombres Moyens” (que podríamos traducir como la regla de los números intermedios), y aparece en el libro “Le Triparty en la Science des Nombres” (1484), del matemático francés Nicolas Chuquet.
Demostremos esta propiedad matemática. La primera desigualdad es equivalente a la desigualdad
, que realizando las multiplicaciones y simplificando las partes iguales a ambos lados, es igual a la desigualdad
. Pero esta es precisamente la hipótesis inicial
. De forma similar se prueba la otra desigualdad.
En consecuencia, hemos demostrado (de forma sencilla) la regla de los números intermedios, por lo que nuestra intuición era efectivamente acertada. Más aún, esto deja claro que las proporciones de la noticia eran incorrectas, como ya sospechábamos.
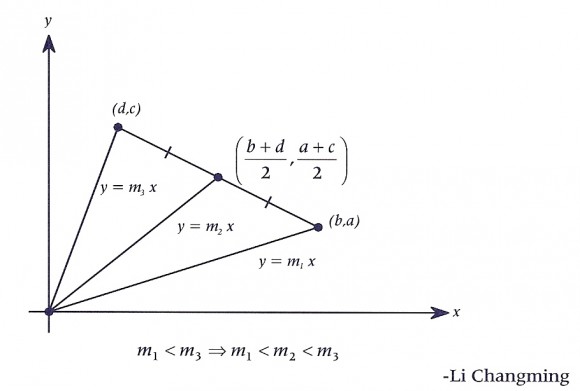
Pero no abandonemos aún en este artículo del Cuaderno de Cultura Científica la demostración de la “regla de los nombres moyens”, puesto que en el libro “Demostraciones sin palabras”, de Roger B. Nelsen, se muestran algunas interesantes demostraciones visuales de este resultado. Aquí os dejo un par de ellas para que las disfrutéis. La primera, de Li Changming, está basada en la pendiente de una recta, ya que dadas dos rectas (que pasan por el origen) e
, la primera está más inclinada que la segunda (“tiene más pendiente”) si
…
Mientras que la segunda, del propio Roger B. Nelsen, utiliza la comparación del área de diferentes rectángulos…
La información real. Una vez resuelta la cuestión desde una perspectiva matemática, me quedaba la cuestión de averiguar la información correcta sobre el parque automovilístico de Bilbao. Estuve buscando por Internet la proporción de coches por cada mil habitantes en la capital vizcaína, y sus barrios, pero no logré localizarla por ninguna parte. En lugar de dejar el tema así, puesto que las matemáticas ya me habían ayudado a saber que había un error, decidí acudir al posible origen de la información, al Ayuntamiento de Bilbao.
Me puse en contacto directamente con el Ayuntamiento de Bilbao y pedí hablar con la persona responsable de estos temas. Me atendió en persona (en el propio ayuntamiento) el subdirector del área de Intervenciones Estratégicas y Aparcamientos, Juan Carlos Acebes, quien no solo estuvo muy cordial, sino que me suministró toda la información que tenía sobre el tema. Un buen ejemplo de atención al ciudadano y de transparencia.
Efectivamente en Bilbao había 385 coches por cada mil habitantes, pero la información sobre los barrios que aparecía en la noticia no se correspondía con los informes del ayuntamiento.
Los datos de los barrios con una mayor proporción de coches eran correctos, salvo en el caso del barrio de Altamira, al que se le asignaba en la noticia un valor menor a 500:
Uretamendi-Iturrigorri, 742 coches por cada 1000 habitantes
Abando A, 609 coches por cada 1000 habitantes
Indautxu A, 527 coches por cada 1000 habitantes
Altamira, 527 coches por cada 1000 habitantes
Begoña, 525 coches por cada 1000 habitantes
Mientras que la información del diagrama de barras fallaba para los barrios con una menor proporción de coches, que eran:
San Francisco, 260 coches por cada 1000 habitantes
Zabala, 273 coches por cada 1000 habitantes
Casco Viejo, 276 coches por cada 1000 habitantes
Santutxu B, 298 coches por cada 1000 habitantes
Este pequeño error periodístico me permitió constatar una vez más que los problemas matemáticos y cotidianos son dos caras de una misma moneda, y que no solo es interesante, sino divertido, mirar ambas.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Bibliografía:
i) Claudi Alsina, Los misterios de la fracción prohibida, SUMA 56, p.39-42, 2007.
ii) Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.
iii) Li Changming, A Geometric Solution to a Problem of Minimization, Mathematics Teacher, vol. 81, no. 1, p. 63. 1988.
iv) Roger B. Nelsen, Proof without Words: Regle des Nombres Moyens, Mathematics Magazine, vol. 67, no. 1, p. 34, 1994.
Esta entrada participa en la edición4.1231056 del Carnaval deMatemáticas,cuyo anfitrión es el blog Scientia.
Resumen de la 4.1231056 edición del Carnaval de Matemáticas | SCIENTIA
[…] 55. La regla de los números intermedios y el parque automovilístico de Bilbao … en el Cuaderno de Cultura Científica. […]