Frank Harary (1921-2005) fue un prolífico matemático, ampliamente reconocido como uno de los ‘padres’ de la teoría moderna de grafos. Usó esta teoría matemática en otras disciplinas, incluyendo la física, la psicología, la sociología, e incluso la antropología.

En esta entrada, se da un ejemplo de utilización de la teoría de grafos para comprender y estructurar la intriga de la ópera bufa Così fan tutte ossia La scuola degli amanti –Así hacen todas o La escuela de los amantes– de Wolfgang Amadeus Mozart, con libreto de Lorenzo da Ponte.

Antes de empezar, ¿qué es un grafo? Un grafo es un conjunto de vértices y de aristas uniendo algunos de los primeros. Se llama dirigido, cuando se añade una orientación a las aristas.

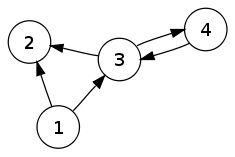
Harary propuso representar mediante esta herramienta la intriga de obras literarias, en particular las relaciones amorosas contenidas en ellas. Por ejemplo, en el grafo de debajo, quedaría representada una relación entre cuatro personas, en la que la primera quiere a la segunda y a la tercera –amor no correspondido–, la segunda no está enamorada de nadie, la tercera no se decide por la segunda o la cuarta, y la cuarta adora a la tercera –amor correspondido–:

De las muchas obras analizadas por Harary, os traigo su estudio “Cosi fan tutte”. A structural study [footnote]HARARY F. (1963). «COSI FAN TUTTE» – A STRUCTURAL STUDY, Psychological Reports, 13 (2) 466-466. DOI: 10.2466/pr0.1963.13.2.466[/footnote].

Così fan tutte es una obra de intercambios de parejas en el Nápoles del siglo XVIII. Sus personajes principales son: Fiordiligi –dama de Guglielmo–, Dorabella –dama de Ferrando y hermana de Fiordiligi–, Guglielmo –soldado enamorado de Fiordiligi–, Ferrando –soldado enamorado de Dorabella– y Don Alfonso –un viejo filósofo–.

Hay tres momentos destacados en la obra:

1. Ferrando y Guglielmo sostienen que sus damas les serán eternamente fieles. Don Alfonso apuesta que en un día es capaz de demostrar que se equivocan. Los dos soldados aceptan la apuesta: simularán que se marchan a la guerra y luego volverán disfrazados, intentando enamorar cada uno de ellos a la amada del otro.

2. Llegan los dos hombres, disfrazados y comienzan su juego de seducción. Dorabella y Fiordiligi piensan que un simple coqueteo es inofensivo.Guglielmo intenta cortejar a Dorabella, que no se resiste mucho. Al principio, Ferrando tiene menos éxito con Fiordiligi, pero ella acaba cayendo en sus brazos. Don Alfonso, ganador de la apuesta, pide a los soldados que perdonen a sus novias porque Così fan tutte.

3. Se finge una doble boda entre las hermanas y sus nuevos novios. Justo al terminar los falsos enlaces, una música militar anuncia el regreso de Ferrando y Guglielmo. Se descubre el engaño y todo se perdona.

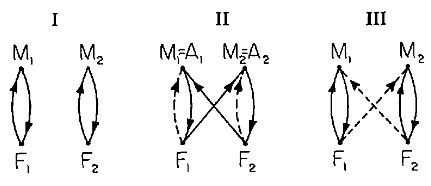
¿Cómo representar la estructura de esta obra usando teoría de grafos? ¿Cómo utilizar la teoría del equilibrio de Fritz Heider en el análisis de la estabilidad de las parejas de esta obra? En [1], Harary argumenta del siguiente modo: llamemos M₁ y M₂ a Ferrando y Guglielmo y F₁ y F₂ a Dorabella y Fiordiligi, respectivamente. Y denominemos A₁ y A₂ a Ferrando y Guglielmo disfrazados. Entonces, cada una de las escenas descritas arriba se pueden representar en forma de grafos por –en este caso, la línea continua significa amor y la discontinua la falta de él–:

Es decir, las escenas I y III son escenas equilibradas –las dos partes que constituyen la relación poseen el mismo carácter dinámico–y la II no lo es: este desequilibrio en la segunda etapa ‘del juego’ conduce a un equilibrio final, al tenderse siempre –según la teoría de Fritz Heider– a recuperar la armonía.

Así que ¡un buen final para la obra! –aunque no es el único equilibrado–.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Esta entrada participa en la VIII Edición del Carnaval de Humanidades, cuyo blog anfitrión es ::ZTFNews.