El problema de la vigilancia de la galería de arte es uno de esos problemas bonitos de las matemáticas. Se puede enunciar de forma sencilla, utilizando además elementos reales de la vida cotidiana. Todo el mundo puede analizar ejemplos concretos de “galerías de arte” que les permitirán entender mejor, con más profundidad, el problema. Tiene una demostración bella, con una parte visual muy atractiva y que puede entender cualquier persona. Los resultados matemáticos relacionados tienen aplicaciones reales. Y existen interesantes generalizaciones del problema, lo que hace que sea un problema vivo.

En 1973 el matemático norteamericano Victor Klee le propuso a su colega Václav Chvátal el conocido como problema de la galería de arte, que pertenece al área de las matemáticas que recibe el nombre de “geometría combinatoria”:
¿Cuál es el mínimo número de guardas, o cámaras de vigilancia, que se necesitan para vigilar una galería de arte?
En primer lugar, expliquemos los datos del problema matemático. ¿Qué es una galería de arte, una cámara de vigilancia o vigilar en este problema?
i) Por una galería de arte se entiende un polígono simple del plano (el problema es bidimensional) formado por n lados, es decir, la galería de arte está rodeada de una cadena cerrada de paredes (segmentos en el plano) que no se intersecan entre sí. Un cuadrado, un octógono o una estrella de seis puntas son ejemplos de polígonos simples del plano, así como los dos siguientes.
ii) La vigilancia de la galería la llevan a cabo o guardas “estáticos” (es decir, guardas que tienen un sitio fijo y no se pueden mover del mismo) o cámaras de vigilancia que cubren cualquier dirección (es decir, 360º), y que están dentro de la galería.
iii) Los lugares vigilados de la galería son trivialmente aquellos puntos de la galería que son visibles por una cámara, o vigilante, es decir, aquellos puntos del interior de la galería poligonal que se pueden conectar mediante un segmento con el punto en el que está la vigilancia.
Veamos algunos ejemplos sencillos de galerías de arte con 3, 4, 5 y 6 lados/paredes (o equivalentemente, vértices)…
Como puede observarse, en los polígonos (galerías de arte) con 5, o menos, vértices, solo es necesario un vigilante, mientras que en los dos ejemplos que tienen 6 vértices hemos necesitado dos.
Un par de resultados sencillos para el problema de la vigilancia de la galería de arte.
A. Cota superior. El número de cámaras mínimo que se necesita para vigilar toda la galería de arte es menor, o igual, que el número de vértices del polígono, ya que si pusiésemos una cámara en cada vértice se vigilaría completamente la galería. De hecho, son demasiadas cámaras como puede comprobarse en todos los ejemplos anteriores.
B. Si es polígono que delimita la galería de arte es convexo (eso en matemáticas quiere decir que dados dos puntos cualesquiera del interior del polígono, el segmento que los une sigue estando dentro del polígono, o intuitivamente, que el polígono no tiene “entrantes”), entonces bastaría una única cámara de vigilancia, que podría colocarse en cualquier lugar de la galería.
Pero regresemos al problema de la vigilancia de la galería de arte. Poco después de que Victor Klee lo formulase, en 1975, Václav Chvátal publicó la solución al mismo (que suele también conocerse como el Teorema del vigilante) en la revista Journal of Combinatory Theory. La solución constaba de dos partes.
A. Teorema: Para vigilar una galería de arte poligonal de n vértices son suficientes n/3 cámaras (para ser exactos el número suficiente de cámaras es└n/3┘, el mayor entero que es menor o igual que n/3).
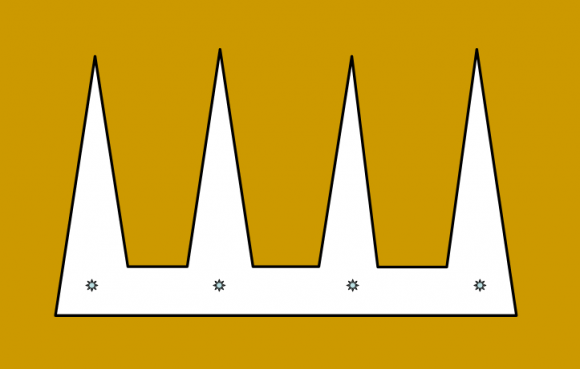
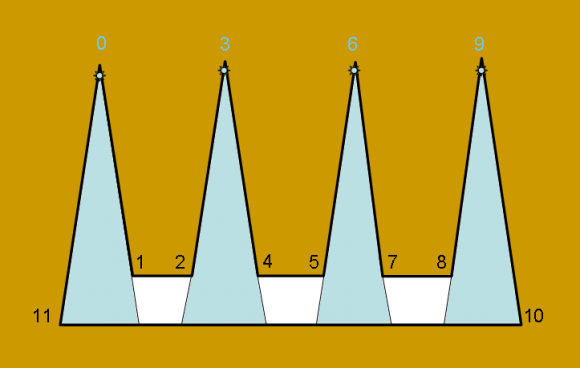
B. Ejemplo: Además, Chvátal construyó un ejemplo para el cual└n/3┘cámaras no solo eran suficientes, sino que además eran necesarias, la galería poligonal peineta.
Por ejemplo, si la peineta tiene cuatro púas (como en la imagen), la galería de arte tiene 12 lados, y el teorema del vigilante dice que son suficientes└12/3┘= 4 cámaras. Pero en este caso también son necesarias, ya que no se podría vigilar con únicamente tres cámaras. Este ejemplo pone de manifiesto que la cota superior, del teorema de Chvátal, de cámaras suficientes para vigilar cualquier galería poligonal, es la mejor cota que se puede obtener (es decir, la más pequeña posible).
El ejemplo de la galería peineta también nos sirve para ver que la táctica de poner una cámara cada tres vértices no sería válida.
Tres años más tarde, en 1978, el matemático Steve Fisk realizaría una bella demostración, mucho más sencilla y breve (ocupaba únicamente una página), de este resultado. Según M. Aigner y G. M. Ziegler, autores de El libro de las demostraciones, esta prueba es merecedora de formar parte de EL LIBRO. El matemático húngaro Paul Erdös (1913-1996) solía hablar de EL LIBRO en el que Dios había escrito las demostraciones perfectas, y más bellas, de todos los teoremas. Veamos los tres pasos de esta demostración:
1. Triangulación. La galería poligonal se puede triangular (es decir, dividir el polígono en triángulos), mediante n-3 diagonales. Por lo tanto, los vértices de la triangulación son los mismos que los del polígono.
Demostración (quien lo desee puede saltarse esta prueba): Vamos a demostrar el resultado por inducción sobre el número n de vértices del polígono. Para n = 3, es trivial puesto que ya es un triángulo. Por lo tanto, vamos a probarlo para n > 3, suponiendo que se verifica para polígonos con un número menor de vértices. Para ello bastará dividir el polígono inicial, mediante una diagonal, en dos polígonos más pequeños (con r y s vértices, tal que r + s = n + 2), puesto que sobre estos existirán, por la hipótesis inductiva, triangulaciones (con r-3 y s-3 diagonales), que juntas constituyen la triangulación del polígono original (con (r-3)+(s-3)+1 = n-3 diagonales).
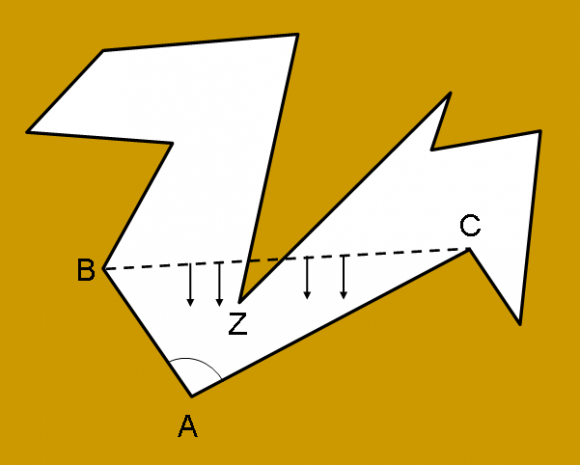
Puesto que la suma de los ángulos interiores de un polígono de n lados es igual a (n-2)180º, existe al menos un vértice –de hecho, al menos tres- cuyo ángulo interior es menor que 180º, que llamaremos A. Denotamos por B y C los vértices adyacentes. Si el segmento BC está contenido en el polígono, entonces separamos el polígono en el triángulo ABC y el polígono restante con n-1 vértices. Por otra parte, si el segmento BC no está contenido en el polígono, entonces el triángulo ABC contendrá otros vértices del polígono.
A continuación, deslizamos el segmento BC hacia A hasta llegar al último vértice Z dentro de ABC. Entonces, AZ estará dentro del polígono y será la diagonal que divida el polígono en los dos más pequeños.
2. Coloración. Se pueden colorear los vértices de la triangulación con tres colores de forma que no haya dos vértices adyacentes con el mismo color (cada vértice de los triángulos que forman la triangulación tendrá un color distinto).
Demostración (quien lo desee puede saltarse esta prueba): De nuevo, vamos a proceder por inducción. Para n = 3 es evidente. Para n > 3, vamos a tomar una diagonal AB de la triangulación, que dividirá al polígono en otros dos más pequeños, que están triangulados y contienen ambos a AB. Por la hipótesis inductiva, se pueden colorear estos dos polígonos triangulados más pequeños, de forma además que A tenga el mismo color en ambas coloraciones, y lo mismo para B. Combinando ambas se concluye.
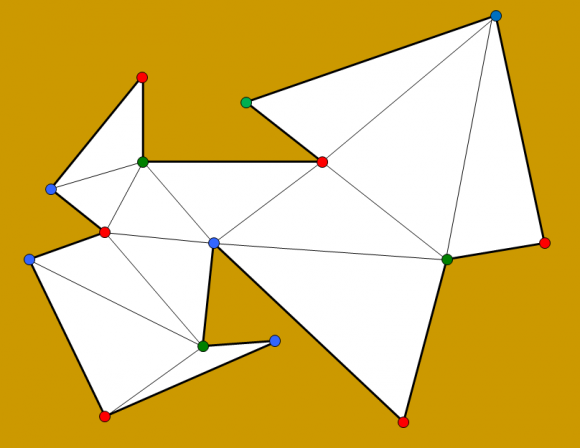
3. Colocación de las cámaras. Teniendo en cuenta que hay n vértices, existe por lo menos un color que colorea como mucho└n/3┘ vértices (puede ser exactamente└n/3┘ vértices o incluso menos, como se muestra en los siguientes ejemplos). Esos vértices son los elegidos para colocar las cámaras. Además, como cada triángulo tiene un vértice de cada color, todos los triángulos son vigilados por cualquiera de los colores, en particular el elegido.
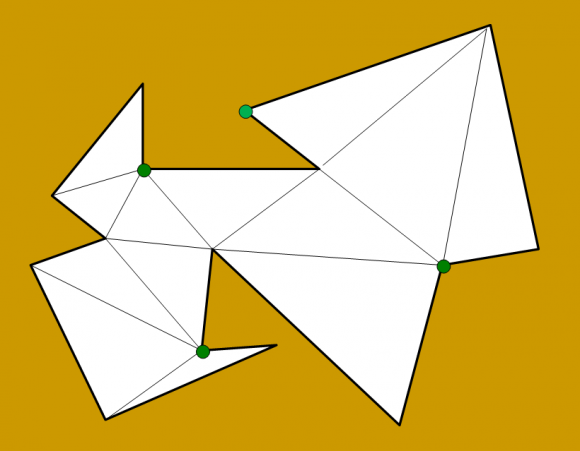
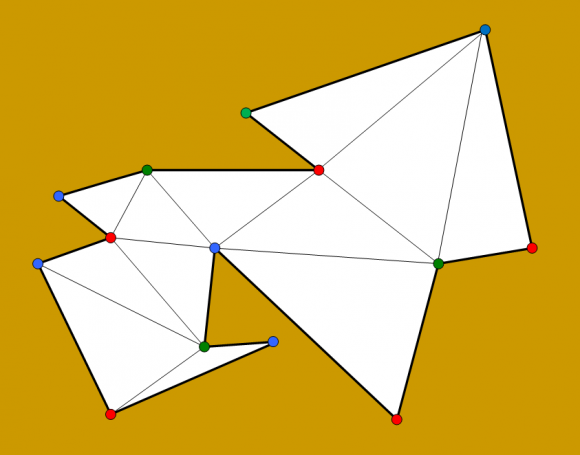
El teorema de la galería de arte (Chvátal-Fisk) nos da la mejor cota superior (es decir, la mas pequeña) del número de cámaras que son suficientes para vigilar una galería de arte, e incluso en qué vértices colocarlas, pero no nos dice cuál es el número mínimo de cámaras que se necesitan para cada galería en concreto. Por ejemplo, en la galería poligonal que estamos utilizando en esta entrada del Cuaderno de Cultura Científica, y en la que hemos dejado cuatro cámaras (correspondientes a los vértices verdes) se podría suprimir incluso una de esas cámaras, y quedarnos solamente con tres. Se ha demostrado que el problema de calcular el número mínimo de cámaras para vigilar una galería de arte (lo suficientemente sofisticada) es un problema computacional de tipo NP fuerte, es decir, no existe un algoritmo eficiente que lo resuelva.
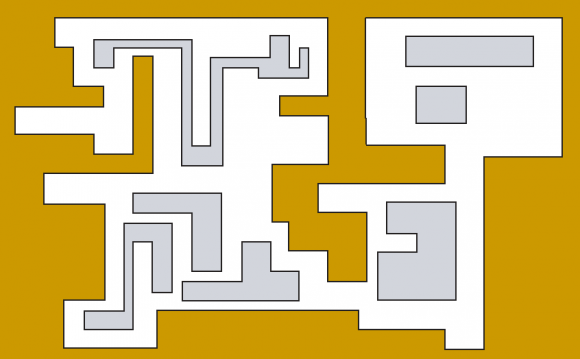
Puesto que la cota dada por Chvátal no se puede mejorar en general, una opción es el estudio de familias concretas de galerías de arte, como por ejemplo, las galerías rectilíneas (u ortogonales), que son aquellas galerías cuyas paredes (los lados del polígono) son paralelas o perpendiculares entre sí.
En 1983, los matemáticos Kahn, Klawe y Kleitman demostraron que las “galerías de arte tradicionales” necesitan menos vigilantes, en concreto demostraron que para galerías ortogonales con n vértices son suficientes└n/4┘cámaras (que es una cota más pequeña que en el caso general). Así mismo, probaron que esa era la mejor cota superior que se podía obtener, puesto que existen galerías para las que se necesitan exactamente└n/4┘ cámaras, como por ejemplo, en la galería de la imagen anterior. También estudiaron el caso de las galerías rectangulares con n salas rectangulares (el caso más clásico), para las cuales son suficientes ┌n/2┐ (es decir, el menor entero mayor o igual a n/2), ya que un guarda situado en el paso entre dos salas las vigila a ambas.
Existen muchas generalizaciones del problema de la vigilancia de la galería de arte. Mencionaremos brevemente cuatro…
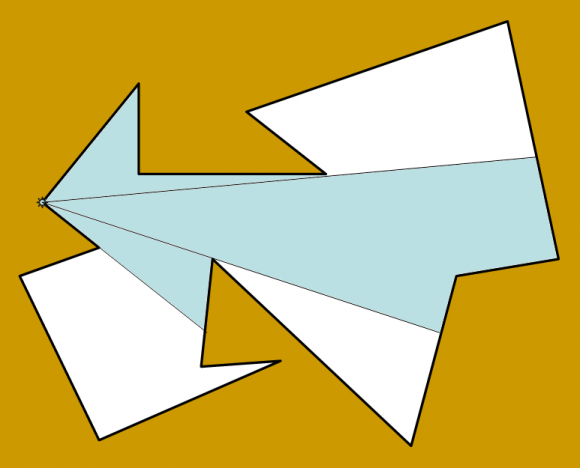
1. Vigilantes móviles. Una variante del problema es cuando el vigilante está colocado en una pared del museo y puede moverse a lo largo de la misma, y en consecuencia, puede vigilar todo aquello visible desde algún punto de esa pared. ¿Cuántos “guardas de pared” hacen falta para vigilar una galería de arte? El matemático Godfried Toussaint construyó un ejemplo en el que eran necesarios└n/4┘guardas de pared (véase la imagen) y conjeturó que, salvo para algunos poco polígonos,└n/4┘ guardas de pared serían suficientes.
2. Galerías con “agujeros”. Otra de las generalizaciones que se están estudiando es el caso de las galerías de arte con “agujeros”, es decir, con zonas interiores que impiden la visibilidad de los guardas (paredes, habitaciones interiores, etc). Se han obtenido muchos resultados para galerías con “agujeros”, ya sean de formas poligonales generales, ortogonales o vigiladas con guardas de pared (para más información véase el artículo sobre recientes resultados en problemas de galerías de arte de T. Shermer, o la conferencia de Hemanshu Kaul).
3. La ruta del vigilante. Otro problema estudiado es el de la determinación de la ruta cerrada que deberá seguir un vigilante, en su ronda nocturna, para que siendo de mínima longitud pueda vigilar toda la galería de arte.
4. La vigilancia vigilada. Si los ladrones de una galería de arte neutralizan una cámara, o a un vigilante, podrán trabajar en su zona de vigilancia. Por ese motivo se han planteado el mismo problema de la vigilancia de la galería de arte, pero de forma que cada vigilante sea vigilado a su vez por alguno de los otros vigilantes.

Y existen muchas otras generalizaciones, la vigilancia del exterior de una fortaleza, la vigilancia de una prisión (exterior e interior), que los vigilantes solo tengan una visión de 180º, que las paredes de la galería sean curvas, el problema tridimensional de la galería de arte o problemas de iluminación, con o sin espejos.
Pero no me gustaría terminar sin mencionar que el interés del teorema de la galería de arte, y resultados relacionados, no es tan solo por su belleza matemática, sino también por sus aplicaciones en ámbitos como la robótica, la vigilancia, las redes de sensores, la planificación de movimientos, el diseño por ordenador, la captura de modelos digitales, el reconocimiento de patrones, o la arquitectura (asistida por ordenadores), como se menciona en algunas de las referencias de la bibliografía.
Bibliografía
1.- Václav Chvatal, A Combinatorial Theorem in Plane Geometry, Journal of Computorial Theory (B) 18, pp 39-41, 1975.
2.- Steve Fisk, A Short Proof of Chvatal’s Watchman Theorem, Journal of Combinatorial Theory, Series B 24, pp 374, 1978.
3.- Martin Aigner, Günter M. Ziegler, El libro de las demostraciones, Nivola, 2005.
4.- J. O’Rourke, Art Gallery Theorems and Algorithms, Oxford University Press, London, New York, 1987.
5.- Joseph Malkevitch, Diagonals (parts I, II), Feature Column (AMS)
6.- J. Kahn, M. Klawe, and D. Kleitman, Traditional Galleries Require Fewer Watchmen, SIAM J. Alg. Disc. Meth., Vol 4, No. 2, pp 194-206, 1983.
7. T. Shermer Recent Results in Art Galleries, Proceedings of the IEEE, vol. 80, 9, pp. 1384-1399, 1992.
8. Hemanshu Kaul, The art galley problem (conferencia)
9. Gregorio Hernández Peñalver, Iluminación y vigilancia en las Galerías de Arte, UPM.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Esta entrada participó en la Edición 4.1231056256 del Carnaval de Matemáticas., cuyo blog anfitrión fue Cuentos Cuánticos resultando elegida mejor post del carnaval.










Joserra Marcaida
Buenísimo el artículo, enhorabuena!!
Raúl Ibáñez
Querido Joserra, muchas gracias.
Un abrazo, Raúl.
Anxo
He encontrado este (interesante) artículo a través de Meneame, y me ha sorprendido un párrafo:
Anxo
El párrafo que quería comentar (me he liado con las etiquetas) es: «Por ejemplo, en la galería poligonal que estamos utilizando en esta entrada del Cuaderno de Cultura Científica, y en la que hemos dejado cuatro cámaras (correspondientes a los vértices verdes) se podría suprimir incluso una de esas cámaras, y quedarnos solamente con tres»»
Raúl Ibáñez
Querido Anxo,
Muchas gracias por tus comentarios. Efectivamente, en ese ejemplo que menciono tan solo se necesitarían dos cámaras para vigilar la galería de arte completamente. Para que fueran tres, por ejemplo se tendría que tener un diseño con el saliente de arriba a la izquierda más inclinado hacia la derecha.
Muchísimas gracias, 🙂
Un abrazo, R.
Josep
Muy interesante. Muchas gracias.
Raúl Ibáñez
Querido Josep, muchas gracias.
Un abrazo, R.
Alexander
Definitivamente, este es de esos articulos que como matemático sientas orgullo y que esta carrera ha valido la pena. Por otro lado, si la demostración ha sido merecedora de formar parte de EL LIBRO es porque definovamente Dios es matemático, o al menos el mejor de los geometras. Excelente articulo, me ha gustado.
Raúl Ibáñez
Muchas gracias Alexander,
Me alegro mucho de que te haya gustado.
Gracias, 🙂
Un fuerte abrazo, Raúl.
Carnaval de Matemáticas. Edición 4.1231056256–El resumen | Cuentos Cuánticos
[…] Teorema de la galería de Arte […]
Cómo sorprenderte con un problema que parece simple: Solución al acertijo de los gatos y los rincones | Cifras y Teclas
[…] de Arte, de mi colega Gregorio Hernández Peñalver. También es muy recomendable la entrada Teorema de la galería de arte de Raúl Ibáñez. Ya en inglés, puedes consultar el libro Art Gallery and Illumination Problems, […]
Jofeye
Precioso, e ¡inspirador!
Enhorabuena por esta entrada, Raul
El teorema de la galería de arte: Daniel G. Andújar en el museo. – Culturaca
[…] de la galería de arte», Cuaderno de cultura científica (24/1/2014), descarga sin paginación (https://culturacientifica.com/2014/01/29/teorema-de-la-galeria-de-arte; acceso, […]
Una bella demostración del LIBRO – Cuaderno de Cultura Científica
[…] En la sección Matemoción del Cuaderno de Cultura Científica ya incluimos hace un tiempo una de esas elegantes demostraciones que pertenecen a El Libro de las demostraciones, una hermosa prueba del conocido como Teorema de la galería de arte. […]
El problema de la plantación de árboles en filas – Cuaderno de Cultura Científica
[…] A. Teorema de la galería de arte […]
David
Enhorabuena por estos artículos, a algunos nos rejuvenece las neuronas, y nos recuerda la belleza, potencia y utilidad de las mates. Observación: En los ejemplos del principio, en el polígono de 6 vértices (abajo a la derecha) es suficiente con una. No contradice nada, solo que queda un poco «mal» en ese contexto, o habría que explicar mas cosas, como que, entiendo yo, que en la introducción se quiere hablar de cámaras en los vértices.
Omar Arturo Alvarez Zaleta
Muy bueno, interesante el problema de geometría y su relación con la combinatoria .
Excelente publicación.