Existen dos matemáticos por los que siento cierta admiración y de los que hemos hablado en varias ocasiones en la sección Matemoción del Cuaderno de Cultura Científica, son los ingleses Arthur Cayley (1821-1895) y James J. Sylvester (1814-1897), que además tuvieron una profunda relación científica y de amistad.

Sobre el primero acabo de terminar una biografía, “Cayley, el origen del álgebra moderna” para la colección Genios de las matemáticas de la editorial RBA, con cuya escritura he aprendido y disfrutado mucho. Sin embargo, en esta entrada no vamos a hablar de Arthur Cayley, sino de su colega y amigo James J. Sylvester, y de un problema que formuló en 1893, en la revista Educational Times.
Problema 11851: Demostrar que no es posible colocar cualquier número finito de puntos (en el plano) de forma que cada recta que pase por dos de ellos también pase por un tercero, salvo que todos los puntos estén contenidos en la misma recta.
Este problema, conocido en ocasiones como el problema de la línea de Sylvester o simplemente el problema de Sylvester, estaba relacionado con un problema más general, que suele recibir diferentes nombres, entre ellos, el problema de la plantación de árboles en filas, el problema del huerto o el problema de los puntos y las líneas, sobre el que estuvo trabajando Sylvester desde la década de 1860 hasta su muerte. En su versión general el problema se puede plantear así.
Problema: ¿Cómo pueden distribuirse n puntos en el plano (o quizás, n árboles en un huerto) formando filas, cada una de las cuales contiene exactamente k puntos (respectivamente, árboles), con el objetivo de obtener el mayor número de filas posibles? ¿Y cuál ese mayor número de filas posibles para cada n y k?
Sylvester había trabajado en la versión clásica en la cual las filas estaban formadas por tres árboles, es decir, el caso k = 3, como podemos observar en los problemas que planteó en Educational Times, en los años 1867 y 1886. Por ejemplo, en el problema 2473 (1867), que podéis ver en la imagen de abajo, planteó dos cuestiones: i) ¿Cómo plantar 81 árboles para que formen 800 filas con 3 árboles en cada fila?; ii) ¿Cómo plantar 10 árboles para que formen 10 filas con 3 árboles en cada fila?

Pero este era un problema que interesaba a más personas. Por ejemplo, como se menciona al final del problema 2473, el actuario inglés Wesley Woolhouse (1809-1893), editor de la famosa revista de matemática recreativa The Lady’s and Gentleman’s Diary, había publicado en la revista de problemas matemáticos The Mathematician que 15 puntos (árboles) podían ser colocados formando 26 filas, con 3 puntos (árboles) en cada fila.
Aunque la primera publicación en la que se mencionan problemas de plantación de árboles en filas fue el libro Rational Amusement for Winter Evenings (1821), de John Jackson, en el que se dedica todo un “capítulo” precisamente a estos problemas, “árboles plantados en filas”.

Pero volvamos al problema de la línea de Sylvester (problema 11851 de Educational Times). Ni Sylvester, ni sus contemporáneos, consiguieron demostrar que no es posible colocar cualquier número finito de puntos en el plano de forma que cada recta que pase por dos de ellos también pase por un tercero, salvo que todos los puntos estén contenidos en la misma recta.
Cuarenta años después de la formulación del problema en Educational Times, aunque sin ser consciente de la existencia del mismo, el matemático húngaro Paul Erdös (1913-1996) conjeturó que el resultado era cierto, y lo publicó después en forma de problema en la revista American Mathematical Monthly (1943), formulado de la siguiente forma.
Problema de la línea de Sylvester (versión Erdös): Demostrar que si un conjunto finito de puntos del plano no están todos sobre la misma recta, entonces existe una recta con exactamente dos de los puntos.
La solución llegó rápidamente. En 1944 se publicaron dos demostraciones en la revista American Mathematical Monthly. Una de ellas, la del colega y amigo de Erdös, el matemático húngaro Tibor Grünwald, que posteriormente se cambiaría el nombre a Tibor Gallai, (1912-1992). Aunque no fue la primera en publicarse, parece ser que era previa a la publicación del enunciado del problema en la revista por parte de Erdös. La otra prueba era del matemático Robert Steinberg (1922-2014), por aquel entonces estudiante en la Universidad de Toronto (Canada). De esos años debía de ser también la demostración del matemático estadounidense Leroy M. Kelly (1914-2002), que es la que vamos a mostrar en esta entrada.
La demostración de Leroy M. Kelly del problema de Sylvester aparece recogida en El Libro de las demostraciones (Nivola, 2005), de los matemáticos Martin Aigner y Günter M. Ziegler, y de la que escriben que puede considerarse “simplemente la mejor”.
Recordemos que el matemático Paul Erdös solía hablar de EL LIBRO en el que Dios había escrito las demostraciones más bellas de entre todos los teoremas. Esta idea llevó a los matemáticos Martin Aigner y Günter M. Ziegler a escribir El libro de las demostraciones (Proofs from the BOOK) con el objetivo de incluir algunas de esas bellas demostraciones de las que hablaba Paul Erdös.
Dos entradas del Cuaderno de Cultura Científica en la que se recogen otras demostraciones de El libro de las demostraciones son:
A. Teorema de la galería de arte
B. Una bella demostración del Libro
Pero vayamos con la demostración de Kelly del problema de la línea de Sylvester. Es decir, vamos a demostrar que si un conjunto finito de puntos del plano no están todos sobre la misma recta, entonces existe una recta con exactamente dos de los puntos.
Demostración: Llamemos Ω al conjunto finito de los puntos del plano dados y Σ al conjunto de todas las rectas que pasan por al menos dos puntos de Ω. A continuación, consideramos todos los pares (P, r), donde P es un punto de Ω que no está en la recta r, de Σ, y todas las distancias de los puntos P a las rectas r, d(P, r), de todos esos pares. Y consideramos el par (Q, s) que nos da la distancia más pequeña de todas ellas. Ahora, llamemos R a la proyección ortogonal de Q sobre s, es decir, al punto de s más cercano a Q.
Vamos a demostrar que la recta s es la que verifica el resultado, es decir, que tiene exactamente dos puntos de Ω.
Supongamos que no es así y que la recta s tiene al menos tres puntos de Ω. Entonces existirán dos puntos P1 y P2 que están en el mismo lado de la recta s respecto de R y supongamos que P1 es el que está más cerca de R (como se muestra en la imagen), incluido el caso en el que P1 sea el propio R.
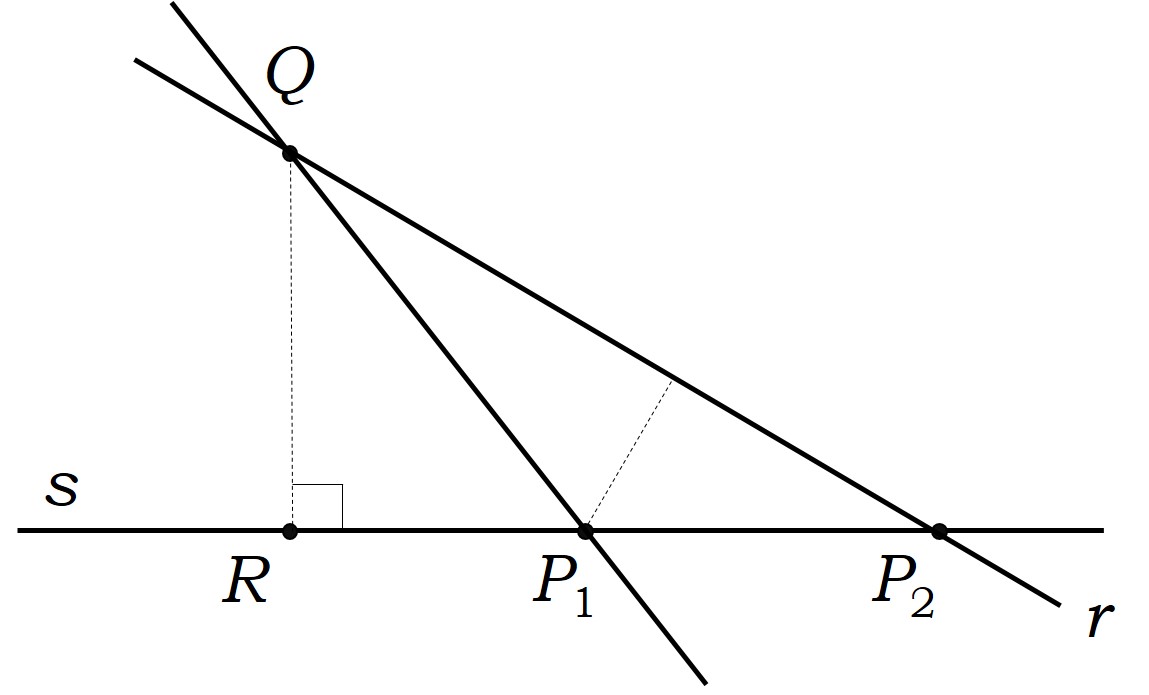
En tal caso, vamos a demostrar que la distancia del punto P1 a la recta r (que es la recta de Σ que pasa por Q y P2) es menor que la distancia de Q a s. Fijémonos en el triángulo QP1P2. Podemos afirmar que:
1. d(P1, P2) < d(Q, P2), ya que el ángulo que tiene como vértice P1 es obtuso (o recto);
2. calculando el área del triángulo desde dos puntos de vista distintos, obtenemos que
![]()
En consecuencia, de 1. y 2. se deduce que d(Q, s) = d(Q, R) > d(P1, r), como habíamos afirmado.
Que la distancia del punto P1, que pertenece a Ω, a la recta r, que pertenece a Σ, sea menor que la distancia de Q a s, es una contradicción con respecto a la elección del par (Q, s). En consecuencia, en la recta s no puede haber nada más que un punto de Ω a cada lado del punto R, es decir, hay dos puntos de Ω en total, como queríamos demostrar. QED
En una siguiente entrega de la sección Matemoción del Cuaderno de Cultura Científica abordaremos la historia de la solución del problema de la plantación de árboles en filas.
Pero vamos a terminar esta entrada con un par de problemas de ingenio del experto inglés en matemática recreativa Henry E. Dudeney (1857-1930). En sus libros, en particular, en Amusements in mathematics (1917), que fue publicado en castellano en tres partes, con el nombre conjunto de Diversiones Matemáticas (El acertijo del mandarín, Los gatos del hechicero y El misterio del muelle), también incluyó problemas de plantaciones de árboles en fila, que él llamó problemas de puntos y líneas.
En Diversiones matemáticas menciona un rompecabezas de este tipo atribuido al matemático inglés Sir Isaac Newton (1643-1727).
Rompecabezas de Newton: plantar 9 árboles de forma que formen 10 filas con 3 árboles en cada fila.
Y el segundo problema de este estilo, que incluimos aquí, lo planteó Dudeney como un problema militar, con una narrativa del problema no muy acertada en mi opinión. Es el problema Turcos y rusos (problema 213 de Amusement in Mathematics), que trasladamos aquí en la versión más simplificada de N. J. A. Sloane, que se recoge en el libro Viajes en el tiempo y otras perplejidades matemáticas, de Martin Gardner.
Turcos y rusos (versión de N. J. A. Sloane): Durante una batalla de la Primera Guerra Mundial, 11 soldados turcos fueron rodeados por 16 soldados rusos. Cada ruso disparó una vez y cada bala pasó exactamente por la cabeza de tres turcos. ¿Cómo estaban colocados los soldados turcos?

Bibliografía
1.- Miodrag S. Petkovic, Famous puzzles of Great Mathematicians, AMS, 2009.
2.- James J. Sylvester, Problem 2473, Mathematical Questions from Educational Times 8, 1867, 106-107.
3.- James J. Sylvester, Problem 2572, Mathematical Questions from Educational Times 45, 1886, 133-134.
4.- James J. Sylvester, Problem 3019, Mathematical Questions from Educational Times 45, 1886, 134.
5.- James J. Sylvester, Problem 11851, Mathematical Questions from Educational Times 59, 1893, 98-99.
6.- John Jackson, Rational Amusement for Winter Evenings, Longman, Hurst, Rees, Orme and Brown, 1821.
7.- H. S. M.Coxeter, A Problem of Collinear Points, The American Mathematical Monthly, Vol. 55, No. 1, 1948, 26-28.
8.- L. M. Kelly, W. O. J. Moser, On the Number of ordinary lines determined by n points, Canad. J. Math. 10, 1958, 210-219.
9.- Martin Aigner, Günter M. Ziegler, El libro de las demostraciones, Nivola, 2005.
10.- Jiri Herman, Radan Kucera, Jaromir Simsa, Counting and Configurations, Canadian Mathematical Society, Springer, 2003.
11.- Henry E. Dudeney, El misterio del muelle (Diversiones matemáticas III), Biblioteca Desafíos Matemáticos, RBA, 2008.
12.- Martin Gardner, Viajes en el tiempo y otras perplejidades matemáticas, Biblioteca Desafíos Matemáticos, RBA, 2007.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Hitos en la red #187 | Enlace Recomendado | Naukas
[…] El problema de la plantación de árboles en filas […]
El problema de la plantación de árboles en filas (2) – Cuaderno de Cultura Científica
[…] anterior entrada en el Cuaderno de Cultura Científica, El problema de la plantación de árboles en filas, terminaba con dos problemas de ingenio propuestos por el experto inglés en matemática recreativa […]