Casi todos los domingos del invierno de 1933, un pequeño grupo de estudiantes se reunía en algún lugar (un parque o un café) de Budapest para hablar de matemáticas. El especial grupo al que me refiero estaba formado, entre otras personas, por Paul Erdős (1913-1996), Esther Klein (1910-2005), Márta Svéd (¿1910?-2005), George Szekeres (1911-2005) y Pál Turán (1910-1976).

En una de estas reuniones, Esther propuso el siguiente problema:

Dados cinco puntos en el plano en posición general, demostrar que cuatro de ellos forman un cuadrilátero convexo.

Tras dejar al resto del grupo un tiempo para reflexionar sobre el problema, Esther explicó a sus colegas la demostración que ella había pensado.

En 1935 Erdős y Szekeres publicaron un artículo en el que se generalizaba el resultado de Esther (ver [1]); es uno de los trabajos fundamentales de la geometría combinatoria. Paul Erdős denominó el problema original como “El problema del final feliz” porque Esther y George se casaron en 1937… ¿tras conocerse mejor gracias a este enunciado?

Empecemos por aclarar los conceptos involucrados en la proposición de Esther. Que varios puntos del plano estén en posición general significa que no existe ningún subconjunto formado por tres de ellos que sean colineales. Un cuadrilátero es convexo si todos sus ángulos interiores son menores que 180 grados.

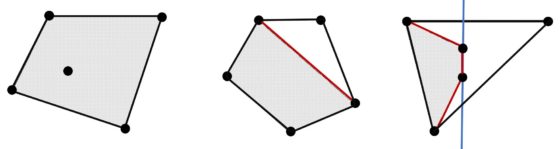
La solución de Esther se basaba en que existen tres formas diferentes en las que un polígono convexo encierra cinco puntos. Dicho de otra manera, dados cinco puntos en posición general, su envolvente convexa puede ser uno de los tres polígonos siguientes:

1. puede ser un cuadrilátero cuyos vértices son cuatro de los puntos del conjunto inicial y que deja en su interior el punto restante. En este caso, la solución ya es inmediata;

2. la envolvente convexa puede ser un pentágono cuyos vértices son los cinco puntos dados. Entonces cuatro de esos puntos pueden conectarse para formar un cuadrilátero convexo;

3. finalmente, si la envolvente es un triángulo, los dos puntos que quedan dentro de la figura definen una recta que divide el triángulo en dos partes. En una de ellas hay dos puntos y en la otra uno de los del conjunto de cinco puntos inicial. Estos dos puntos y los interiores forman automáticamente un cuadrilátero convexo.

Como hemos comentado antes, Erdős y Szekeres publicaron en 1935 (ver [1]) una generalización del problema planteado por Esther Klein. El artículo comenzaba del siguiente modo:

El problema que nos ocupa ha sido sugerido por la señorita Esther Klein en relación con la siguiente proposición.

A partir de cinco puntos del plano de los cuales no hay tres en una misma línea recta, siempre es posible seleccionar cuatro puntos que determinan un cuadrilátero convexo.

[…] La señorita Klein sugirió el siguiente problema más general. Dado un entero positivo n, ¿es posible encontrar un número N(n) tal que de cualquier conjunto que contenga al menos N(n) puntos sea posible seleccionar n puntos que formen un polígono convexo?

Hay dos preguntas particulares: (1) ¿existe el número N(n) correspondiente a n? (2) Si es así, ¿cómo se determina el menor N(n) en función de n? (denotamos el menor N por N₀(n)).

En [1] los autores demostraban que el número N(n) existe (para n mayor que 2) y conjeturaban que

basándose en algún caso particular demostrado por otros autores. De hecho, es obvio que N₀(3)=3, Esther Klein demostró que N₀(4)=5 y en [1] se afirma que E Makai probó que N₀(5)=9, aunque no existe evidencia escrita de ello. Años más tarde Szekeres y Lindsay Peters (ver [2]) demostraron con ayuda de un ordenador que N₀(6)=17, reafirmando la conjetura.

Y, de momento nadie ha sido capaz de confirmar o refutar la conjetura. Pero la propuesta se ha reformulado proponiendo la alternativa siguiente (ver, por ejemplo, [4]):

donde la O mayúscula se refiere a la notación de Landau. Confiemos en que pronto se conocerá más sobre esta interesante acotación.

Por cierto, la historia de amor (el “final feliz” entre sus dos colegas, como lo denominaría Erdös) de Esther y George fue larga e incluso poética en su despedida: ambos fallecieron el 28 de agosto de 2005, con una hora de diferencia. Ella tenía 95 años, él 94… y ambos número de Erdös igual a 1.

Referencias

[1] Paul Erdös and George Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935), 463-470.

[2] George Szekeres and Lindsay Peters, Computer solution to the 17-point Erdös-Szekeres problem, ANZIAM J. 48 (2006), 151-164

[3] Pierre-Alain Cherix, Shaula Fiorelli Vilmart, Pierre de la harpe, Polygones convexes : le problème de la fin heureuse, Images des Mathématiques, CNRS, 2014

[4] Sara Freyland, The Happy Ending Problem and its connection to Ramsey theory, Report Uppsala University, 2019

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.