En mi anterior entrada del Cuaderno de Cultura Científica, Las dos culturas de las matemáticas: construir teorías o resolver problemas, estuvimos hablando precisamente de eso, de lo que se conoce como las dos culturas de las matemáticas, construir teorías o resolver problemas.
Dentro del grupo de personas que hacen matemáticas “cuyo objetivo central es resolver problemas” se citaba al matemático húngaro Paul Erdös (1913-1996), considerado “el príncipe de los que resuelven problemas y el monarca absoluto de quienes saben proponer problemas”.

Este brillante y extravagante matemático, en la introducción del artículo Some of My Favourite Problems and Results (Algunos de mis problemas y resultados favoritos), escribe lo siguiente.
Los problemas han sido siempre una parte fundamental de mi vida matemática. Un problema bien elegido puede aislar una dificultad esencial en un área particular de las matemáticas, de forma que el mismo sirva de marca que hay que superar para que se produzca el progreso de esa área. Un problema de apariencia inocente a menudo no da ninguna pista de su verdadera naturaleza. Puede ser como un “malvavisco”, que sirve de delicioso bocado de cardenal proporcionando unos instantes de efímero placer. O puede ser como una “bellota”, que necesite agudos y profundos nuevos conocimientos a partir de los cuales pueda crecer un poderoso roble.
Leyendo estos días sobre algunos de los problemas que planteó y resolvió Paul Erdös, descubrí en el libro Mathematical Diamonds, del matemático canadiense Ross Honsberger (1929-2016), un curioso problema, con una sorprendente y hermosa demostración, que me ha parecido interesante comentaros en esta entrada del Cuaderno de Cultura Científica. Espero que disfrutéis de este problema “malvavisco”, tanto como yo disfruté cuando lo leí.
En la década de 1940, el matemático Paul Erdös estaba estudiando y planteando problemas relacionados con diferentes propiedades y estructuras de conjuntos de puntos del plano. Así, por ejemplo, en 1943 planteó en la revista American Mathematical Monthly el problema “Demostrar que, si un conjunto finito de puntos del plano no están todos sobre la misma recta, entonces existe una recta con exactamente dos de esos puntos”. Sin ser consciente de ello, Erdös reformuló el problema de la línea de Sylvester, que en su momento comentamos en la entrada El problema de la plantación de árboles en filas.
Pero vayamos al problema que nos interesa hoy. En el año 1945, Erdös planteó lo siguiente.
Problema (Paul Erdös): Si dado un conjunto infinito de puntos del plano, las distancias entre ellos son todas números enteros (podemos entender naturales), entonces todos los puntos están en una misma línea recta.
Claramente, si tomamos una recta cualquiera del plano podemos considerar una colección infinita de puntos tal que la distancia entre cualquier par de puntos sea un número natural, sin más que partir de un punto inicial e ir tomando hacia izquierda y derecha los puntos que están a una distancia unidad del inmediatamente anterior (como los puntos rojos que están sobre la recta roja del plano en la siguiente imagen). Lo sorprendente de la afirmación de Erdös en el enunciado del problema es que esa es la única forma de obtener una colección infinita de puntos tal que las distancias entre cualesquiera dos de ellos es siempre un número natural.

La demostración del problema es sencilla, sorprendente e ingeniosa, yo diría más, es una bella demostración. El argumento de la misma se centra en una curva de la familia de curvas cónicas, la hipérbola.
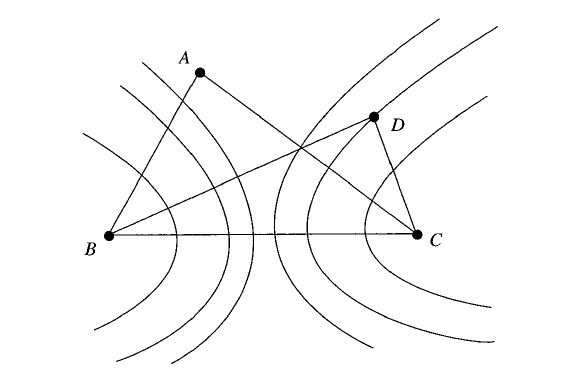
El argumento de la demostración de Erdös es por “reducción al absurdo”. Supongamos que el resultado no fuese cierto, es decir, que existe un conjunto infinito de puntos del plano S, tal que la distancia entre cualesquiera dos de ellos es un número natural y que existen tres puntos A, B y C, del conjunto S, que no son colineales, no están en la misma recta. En ese caso, esos tres puntos determinan un triángulo del plano. Denotemos por a, b y c las longitudes de los lados del mismo, opuestas a los vértices A, B y C, respectivamente, que sabemos, por hipótesis, que son números naturales.
Ahora, consideremos otro punto cualquiera D del conjunto S (recordemos que este conjunto tiene infinitos puntos). Teniendo en cuenta que las distancias de D a los tres puntos A, B y C son también enteras, por estar todos en S, el matemático húngaro demostró que solamente puede haber un número finito de puntos del plano candidatos a ser D. En conclusión, S no puede ser infinito. Veámoslo.
El punto D no es uno de los vértices del triángulo, que son los puntos A, B y C, por lo que como mucho puede estar en una de las rectas que contienen a los lados del triángulo, AB, AC y BC. Es decir, podemos afirmar que existen (al menos) dos rectas, de las tres que contienen los vértices del triángulo, en los cuales no está el punto D. Supongamos que esas rectas, en las que no está el punto D, son las que contienen a los lados AC y BC.
Las distancias del punto D a los puntos B y C son números naturales, ya que los tres están en S, por lo tanto, la diferencia entre ellas |BD – CD| es también un número natural o cero. Como el punto D no está en la recta de BC, la desigualdad triangular (“la suma de las longitudes de dos lados cualesquiera de un triángulo es siempre mayor que la longitud del otro lado”) nos dice que |BD – CD| < BC = a.
Juntando todo lo anterior, tenemos que |BD – CD| = k, donde k es uno de los números enteros 0, 1, 2, …, a – 1. Por lo tanto, D es un punto que pertenece a la hipérbola con focos B y C, y tal que la diferencia de la distancia de sus puntos a los focos es k. Es decir, D está en una de las a hipérbolas que forman la familia de hipérbolas de focos B y C, y diferencias constantes k = 0, 1, 2, …, a – 1.
Antes de continuar, recordemos brevemente la propiedad métrica, que estamos mencionando, de las hipérbolas. En general, todas las curvas cónicas se pueden caracterizar mediante una propiedad métrica. Por ejemplo, la circunferencia está formada por los puntos del plano que equidistan, es decir, que están a la misma distancia, de un punto fijo, el centro de la misma.
En el caso de la hipérbola, existen dos puntos destacados, los focos (F1 y F2 en la siguiente imagen), y cada hipérbola está caracterizada por estar formada por los puntos P del plano tales que la diferencia de las distancias a los focos |PF1 – PF2| es una constante k, para cada hipérbola. Luego, dados dos focos F1 y F2, para cada constante k se obtiene una hipérbola como la de la siguiente imagen (con dos ramas). Para k = 0 se obtendría una hipérbola degenerada, que es la recta mediatriz del segmento F1F2, es decir, los puntos que están a la misma distancia de cada uno de los focos.
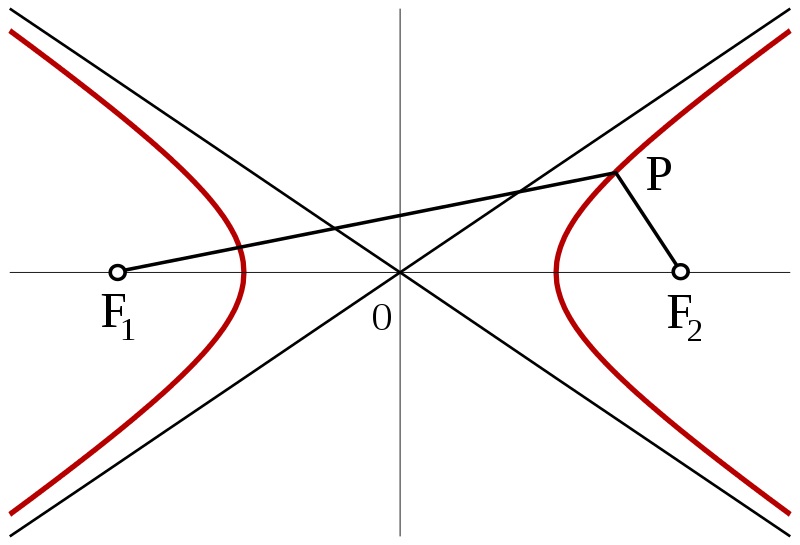
Regresemos a la demostración. Hemos probado que como el punto D no está en la recta de BC, D está en alguna de las a (que es un número natural) hipérbolas que forman la familia de hipérbolas de focos B y C, y diferencias constantes k = 0, 1, 2, …, a – 1. De la misma forma, tendrá que ser cierto que, como el punto D no está en la recta que contiene a AC, D está en alguna de las b (que también es un número natural) hipérbolas que forman la familia de hipérbolas de focos A y C, y diferencias constantes m = 0, 1, 2, …, b – 1.
Como dos hipérbolas cualesquiera se intersecarán, como mucho, en 4 puntos distintos, entonces las a hipérbolas de la primera familia y las b hipérbolas de la segunda, se intersecarán a lo sumo en 4ab puntos del plano. Es decir, solo existe un número finito de posibles puntos del plano, (como mucho) 4ab, candidatos a ser D. Esto nos lleva a una contradicción con el hecho de que S es un conjunto infinito, y D es un punto del conjunto, también infinito, S – {A, B, C}, ya que hemos probado que solo hay un número finito de posibles puntos D. Por lo tanto, cualesquiera tres puntos A, B y C, de S, deberán estar alineados, luego los puntos de S están sobre la misma recta.
Q.E.D. (Quod erat demonstrandum)

Pero, como suele ocurrir en matemáticas, no nos paramos aquí. Una vez demostrado el problema de Erdös (Si dado un conjunto infinito de puntos del plano, las distancias entre ellos son todas números enteros, entonces todos los puntos están en una misma línea recta), podemos preguntarnos qué ocurre con un número finito de puntos. ¿Será posible disponer de un número finito n de puntos, para cualquier n, de forma que las distancias entre cualesquiera dos puntos sean números enteros y no estén todos en una recta?
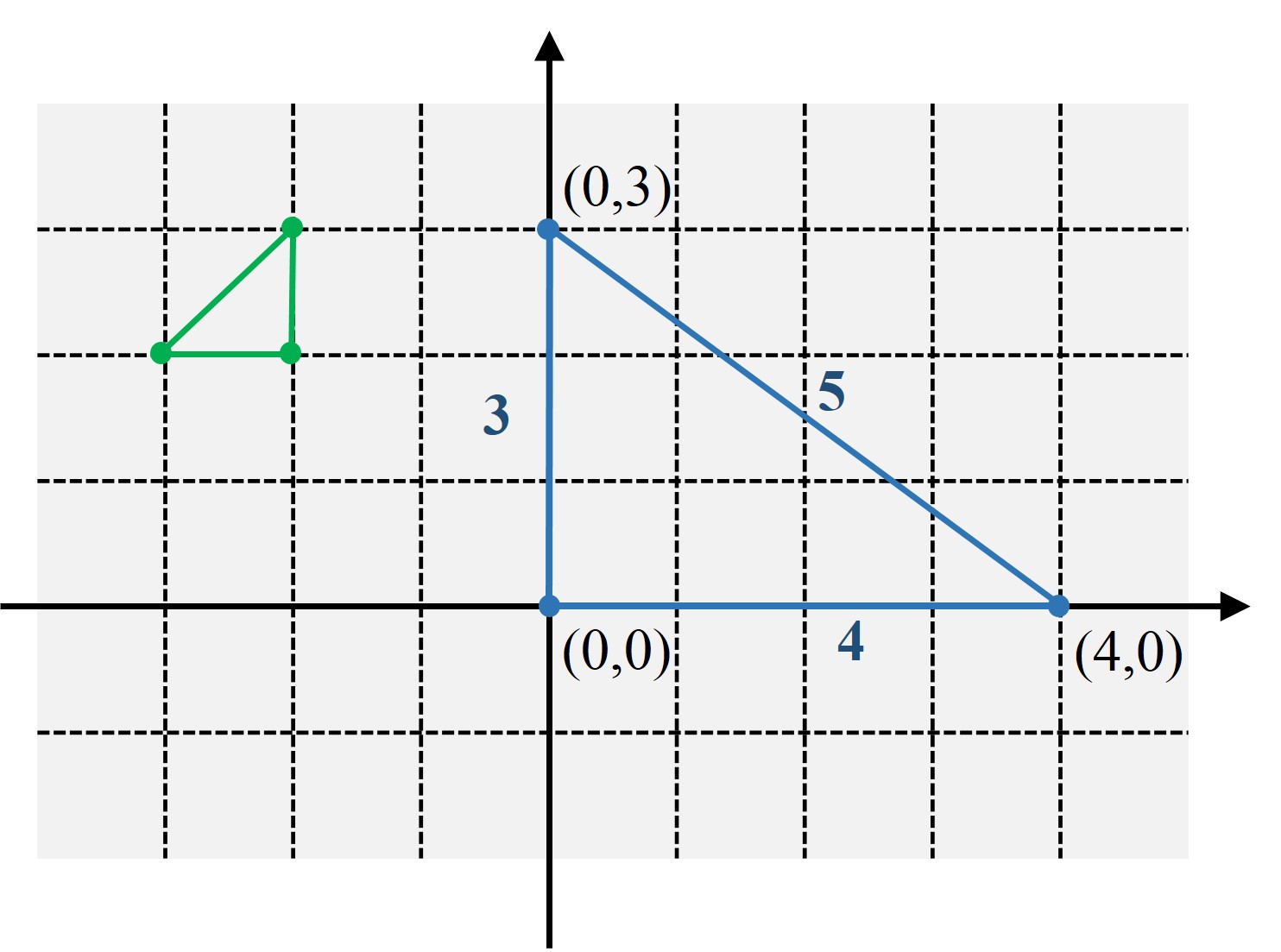
Empecemos planteando el problema para tres puntos. Si consideramos tres vértices de un cuadrado de lado 1, estos no nos valdrán ya que mientras que los lados sí son distancias enteras, en concreto, 1, no lo es la diagonal, cuyo valor es la raíz de 2, sencillamente por el teorema de Pitágoras. Pero este resultado de la geometría clásica nos da una idea para construir un triángulo cuyos tres lados sí sean números enteros. Tomemos una terna pitagórica cualquiera (a, b, c), es decir, a2 + b2 = c2, y construyamos el triángulo rectángulo que tiene por lados esa terna. Por ejemplo, en el plano coordenado los puntos (0, a), (0, 0) y (b, 0). En la imagen siguiente hemos dibujado (en azul) el correspondiente a la terna (3, 4, 5).
Precisamente, el matemático David Silverman, en 1963, utilizó las ternas pitagóricas irreducibles para demostrar que podía construirse un conjunto cualquiera de puntos del plano con distancias enteras entre ellos y que no fuesen colineales. Para empezar, recordemos que una terna pitagórica (a, b, c), es decir, a2 + b2 = c2, se dice que es irreducible si los tres números a, b y c no tienen, dos a dos, divisores comunes. Por ejemplo, la terna (3, 4, 5) es irreducible, pero no (6, 8, 10).
Sean m ternas pitagóricas irreducibles distintas, (ai, bi, ci), para i = 1, 2, …, m. Tomamos el producto P = a1 x a2 x … x am, David Silverman consideró los m + 1 puntos del plano coordenado siguientes:
(0, P) y ((bi / ai) P, 0), para i = 1, 2, …, m.
Como ai divide a P, cada uno de los puntos anteriores tienen coordenadas enteras, el primero está en el eje de ordenadas (eje y) y los demás en el eje de abscisas (eje x). Y, además, los puntos que están en el eje x distan entre ellos un número entero. Para concluir faltaría ver que la distancia entre el punto (0, P) y cualquiera de los otros ((bi / ai) P, 0) es entera. Esa distancia es
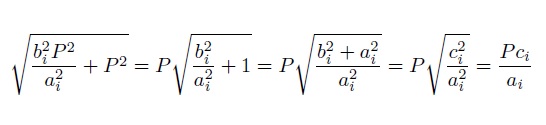
que claramente es entera, ya que ai divide a P.
Además, por ser los triples pitagóricos irreducibles cada punto ((bi / ai) P, 0) es distinto a los demás. Supongamos que existen i y j tales que ((bi / ai) P, 0) = ((bj / aj) P, 0), entonces bi / ai = bj / aj. Luego ai x bj = aj x bi. Como ai y bi no tienen divisores comunes, entonces ai divide a aj y como aj y bj no tienen divisores comunes, entonces aj divide a ai. En conclusión, ai = aj, y de forma equivalente se prueba que bi = bj, lo que implicaría que son el mismo triple pitagórico, lo cual no es cierto.
Por lo tanto, (0,0), (0, P) y ((bi / ai) P, 0), para i = 1, 2, …, m, son m + 2 puntos del plano, no colineales, y que distan entre ellos un número entero.
Efectivamente, el anterior es un ejemplo de un número finito de puntos no colineales que distan entre sí distancias enteras. Sin embargo, podríamos decir que dejan de ser colineales por la mínima ya que todos están en la misma recta, el eje x, salvo el punto (0, P).
En el libro Combinatorial Geometry in the plane, de Hugo Hadwiger y Hans Debrunner se obtiene un resultado más general. Se demuestra que, para cada n, existe un conjunto finito de n puntos del plano, de forma que las distancias entre cualesquiera dos puntos son números enteros y no solo no están todos en una misma recta, sino que, además, no hay tres puntos que sean colineales. Pero esa demostración la dejamos solo para las personas que estén interesadas en ir un poco más allá. Se puede leer en cualquiera de los libros mencionados, Mathematical Diamonds y Combinatorial Geometry in the plane.

Bibliografía
1.- William Timothy Gowers, Las dos culturas de las matemáticas, La GACETA de la RSME, vol. 7.2, pag. 371–386, 2004 (publicado originalmente como The Two Cultures of Mathematics, en Mathematics: Frontiers and Perspectives, V.I. Arnold, M. Atiyah, P. Lax y B. Mazur (eds.), AMS, 1999).
2.- Raúl Ibáñez, La cultura científica o la misteriosa identidad del señor Gauss, CIC-Network, n. 8, pag. 14-17, 2010. (versión online en el Cuaderno de Cultura Científica)
3.- Paul Erdös, Some of My Favourite Problems and Results, perteneciente al libro The Mathematics of Paul Erdös I, editado por Ronald L. Graham y Jaroslav Nesetril, Springer-Verlag, 1997.
4.- Ross Honsberger, Mathematical Diamonds, MAA, 2003.
5.- Hugo Hadwiger, Hans Debrunner, Combinatorial Geometry in the Plane, Dover, 1964.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Javier
Este resultado no deja de sorprenderme (vaya por delante que no tengo conocimientos avanzados de matemáticas). Si lo he entendido bien, viene a decir que no podemos construir un conjunto infinito de puntos sobre el plano de forma que se encuentren a distancia entera dos a dos. Sin embargo, podemos construir un conjunto de estas características con n puntos (es decir un número finito), pero con n tan grande como queramos.
No sé, pero a un nivel intuitivo no puedo evitar percibirlo como una contradicción. Una paradoja.
Raúl Ibáñez
Querido Javier,
Lo has entendido perfectamente. A mi me parece un resultado curioso, y además con una hermosa y sencilla demostración. Efectivamente para un conjunto n de puntos, tan grande como queramos, se pueden obtener con distancias enteras, pero el resultado no es cierto para infinitos puntos (salvo la recta). El salto entre un número finito de puntos, por grande que sea, e infinitos puntos es bestial, y este resultado es una muestra más.
Un abrazo, Raúl.
Felo
Creo que el problema está mal formulado. Si condideras el subanillo de C Z(i) = { a+bi: a,b enteros }, biyectable trivialmente con un subconjunto del plano, tienes un claro contraejemplo
Felo
Creo que debes especificar más hipótesis. Tomando el subconjunto del plano K = {(a,b): a,b enteros } ( biyectable con los enteros gaussianos ) tenemos un claro contraejemplo de tu enunciado
Ramazotti
Tu observación es incorrecta, puesto que si bien (1,0) y (0,1) pertenecen a K, d((1,0),(0,1)) =√2 que no pertenece a Z. Saludos!
El negro es un color matemático — Cuaderno de Cultura Científica
[…] leerse las entradas Las dos culturas de las matemáticas: construir teorías o resolver problemas, Un dulce problema de Paul Erdös o El problema del final feliz), o la enseñanza de las matemáticas en un instituto de secundaria y […]