Mi anterior entrada en el Cuaderno de Cultura Científica, El problema de la plantación de árboles en filas, terminaba con dos problemas de ingenio propuestos por el experto inglés en matemática recreativa Henry E. Dudeney (1857-1930), en su libro Amusements in mathematics –Diversiones matemáticas- (1917). Uno de ellos era el conocido como Rompecabezas de Newton.
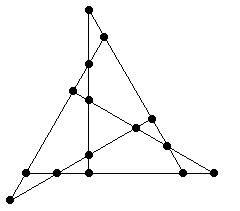
Rompecabezas de Newton: plantar 9 árboles de forma que formen 10 filas con 3 árboles en cada fila.
Os animo a quienes estáis leyendo esta entrada a que intentéis resolver el rompecabezas de Newton, antes de mirar la solución que mostraré más adelante.

Este problema de ingenio está relacionado con la familia de problemas de ingenio llamados de plantación de árboles en filas o problemas de puntos y líneas. La formulación general de estos problemas es la siguiente.
Problema: ¿Cómo pueden distribuirse n puntos en el plano (o quizás, n árboles en un huerto) formando filas, cada una de las cuales contiene exactamente k puntos (respectivamente, árboles), con el objetivo de obtener el mayor número de filas posibles? ¿Y cuál ese mayor número de filas posibles para cada n y k, que denotamos r(n,k)?
El matemático inglés James J. Sylvester (1814-1897) estuvo trabajando en este problema, para el caso clásico de filas formadas por tres árboles, es decir, el caso k = 3, desde la década de 1860 hasta su muerte. El problema de la línea de Sylvester del que hablamos en la anterior entrada formaba parte de esta investigación.
El problema general de determinar la mayor número de filas r(n, k) para n puntos y k puntos por fila no se ha resuelto todavía. Se ha obtenido la solución para algunos casos particulares y también algunas cotas inferiores para r(n, k). Por ejemplo, el propio Sylvester demostró la siguiente cota inferior:
![]()
x
es el número entero más grande que es menor o igual que x, por ejemplo,
5,2
= 5; ó
–3,2
= – 4.
Cuando k = 2 el problema es trivial, ya que cada par de puntos de los n dados forman una recta, luego el máximo número de rectas posibles es el número combinatorio “n sobre 2”, es decir, las formas de elegir dos objetos de un conjunto de n,
![]()
Para el caso clásico de filas de tres árboles, k = 3, la cuestión se complica ya mucho. Como comentaba Martin Gardner en su artículo Problemas de plantación de árboles, del libro Viajes en el tiempo y otras perplejidades matemáticas, este problema está relacionado con diferentes teorías matemáticas, como teoría del diseño, triples de Kirkman-Steiner, geometrías finitas, funciones elípticas de Weierstrass, curvas cúbicas, planos proyectivos, códigos de corrección de errores y muchas otras.
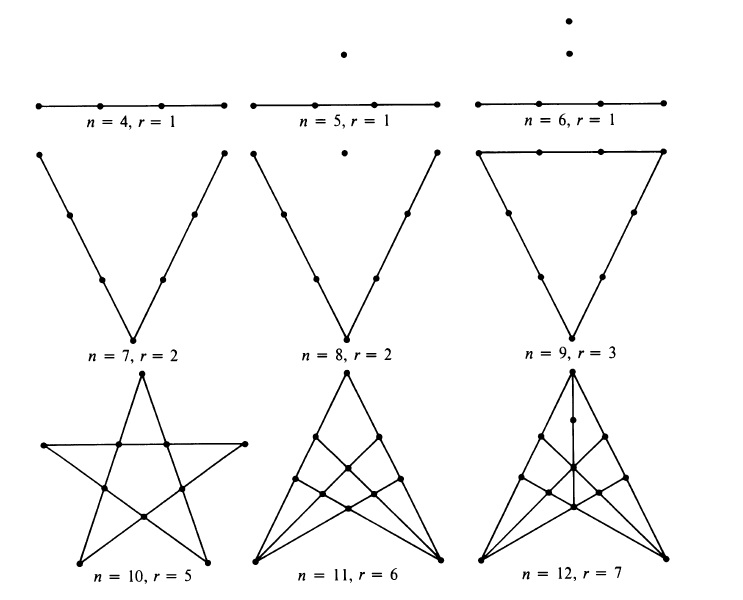
En la siguiente imagen vemos soluciones para un número bajo de puntos, es decir, distribuciones maximales de puntos (resp. árboles) en filas de tres puntos (resp. árboles) para una cantidad de puntos entre 3 y 10, muchos de los cuales aparecen en libros clásicos de problemas de ingenio.

En concreto, el diagrama para el caso de 9 puntos (abajo a la izquierda) es la solución al rompecabezas de Newton.
El diagrama que resuelve el caso de once puntos, es decir, la distribución maximal de 11 puntos, que permite obtener 16 rectas, es la solución del otro problema de ingenio de Henry E. Dudeney (1857-1930), de su libro Amusements in mathematics –Diversiones matemáticas-, que propusimos en la anterior entrada del Cuaderno de Cultura Científica, El problema de la plantación de árboles en filas.
Turcos y rusos (versión de N. J. A. Sloane): Durante una batalla de la Primera Guerra Mundial, 11 soldados turcos fueron rodeados por 16 soldados rusos. Cada ruso disparó una vez y cada bala pasó exactamente por la cabeza de tres turcos. ¿Cómo estaban colocados los soldados turcos?
Es el siguiente diagrama:

El ingeniero Robert H. Macmillan (1921-2015) que era un apasionado de la matemática recreativa, y colaborador habitual de la revista The mathematical Gazette anunció en esta revista en 1946 que se podía obtener una distribución de 12 puntos que permitía obtener 19 rectas. Después Stefan A. Burr, Branko Grunbaum, N. J. A. Sloane, en su artículo The Orchand Problem –el problema del huerto- (1974) demostraron que 19 era maximal, es decir, r(12, 3) = 19. A continuación mostramos la distribución maximal que aparece en el artículo de Burr, Grunbaum y Sloane. Esta distribución simétrica se ha realizado sobre el plano proyectivo, es decir, con puntos del infinito, de hecho, tres de los puntos están en el infinito y una de las rectas es la recta del infinito. Esta solución se puede trasladar al plano normal (euclídeo), pero no es tan sencilla de visualizar, por eso mostramos aquí la del plano proyectivo.
Aprovechemos para recordar que el plano proyectivo es una estructura geométrica que extiende el concepto de plano euclídeo ordinario. En el plano euclídeo dos rectas se intersecan en un punto o son paralelas. El plano proyectivo puede pensarse como el plano euclídeo al que se le añaden “puntos del infinito”, donde se intersecan las rectas paralelas. Por lo tanto, en el plano proyectivo cualesquiera dos rectas se cortan y lo hacen en un único punto. Además, todos los puntos del infinito forman la “recta del infinito”.
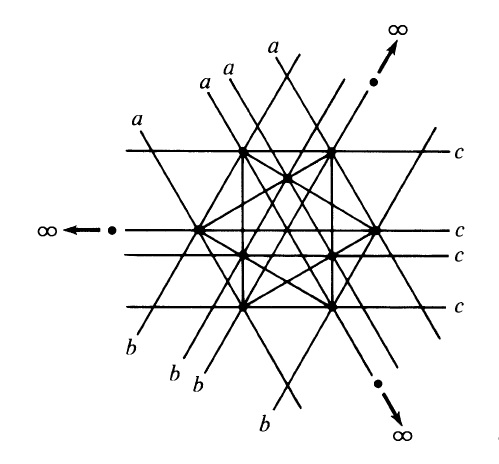
Stefan A. Burr, Branko Grunbaum, N. J. A. Sloane también obtuvieron en su artículo una nueva cota inferior para r(n, k), en concreto:
![]()
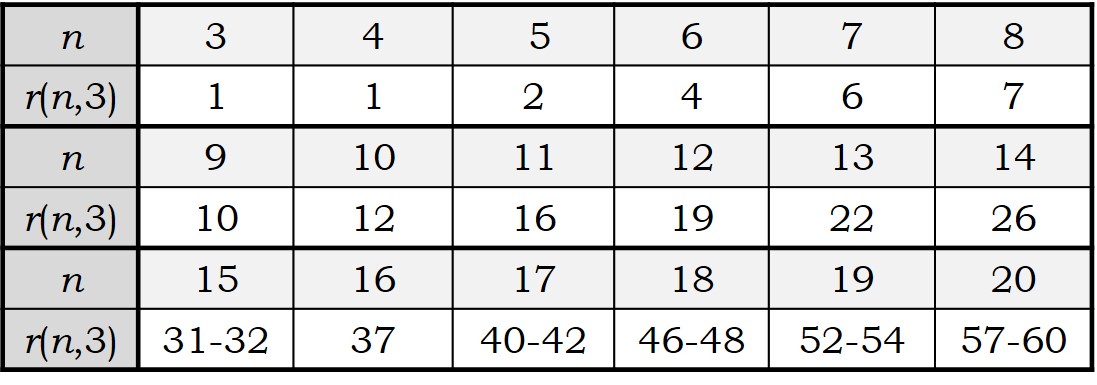
Así, por ejemplo, para las siguientes cantidades de puntos n = 13, 14, 15 y 16, se sabe que la cantidad de rectas, con tres puntos, maximal es mayor, o igual, que 22, 26, 31 y 35, respectivamente.
Recientemente, los matemáticos inglés Ben Green y australiano Terence Tao, han demostrado que la cota inferior para r(n, k) de Burr, Grunbaum y Sloane es también una cota superior, para valores suficientemente grandes de n, y por lo tanto, es el valor exacto de r(n, k), para dichos valores suficientemente grandes de n.
Los números r(n, 3) forman una sucesión de números enteros que aparece en la Enciclopedia On-line de Sucesiones de Números Enteros (The On-Line Encyclopedia of Integer Sequences) como la sucesión A003035.
Los valores que se conocen de r(n, k), para n menor o igual que 20 son los siguientes:
Si aumentamos el número de puntos (o árboles) por línea a cuatro, k = 4, el problema de la plantación de árboles por filas, que ya era complicado para el caso clásico de 3 puntos por fila, se complica más aún.
En la actualidad se ha conseguido calcular el valor de r(n, 4) para n entre 4 y 20.
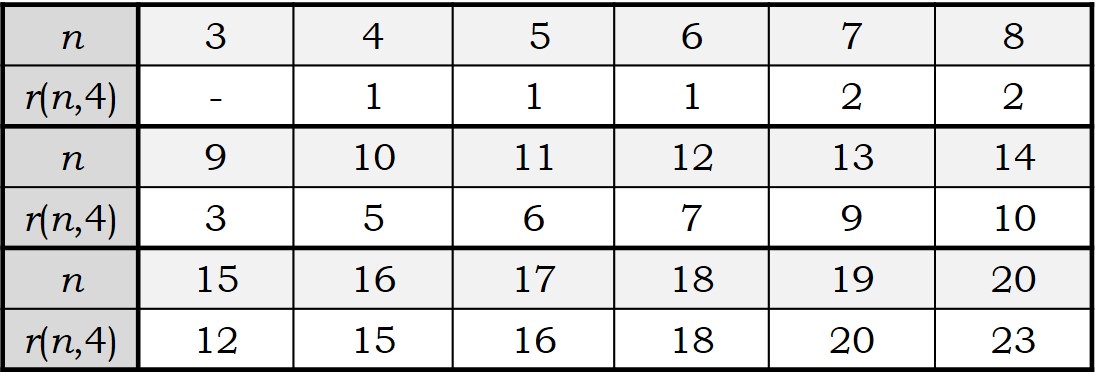
La sucesión de números r(n, 4) es la sucesión A006065 [https://oeis.org/A006065] en la Enciclopedia On-line de Sucesiones de Números Enteros (The On-Line Encyclopedia of Integer Sequences).
Los diseños maximales para valores bajos de n pueden verse en la siguiente ilustración del artículo de Martin Gardner, Problemas de plantación de árboles.
Este tipo de cuestiones han sido utilizadas por muchos expertos en matemática recreativa, como el mencionado Dudeney o el americano Sam Loyd (1841-1911), para crear problemas de ingenio. Por ejemplo, la solución óptima para 16 árboles (n = 16) fue utilizada por Dudeney en el “acertijo del Labrador” de su libro Los acertijos de Canterbury (RBA, 2007).
El acertijo del Labrador: El labrador, de quien Chaucer señaló, “Un verdadero trabajador y muy bueno era él, que vivía en paz y caridad perfectas”, se quejó de que los acertijos no eran para mentes simples como la de él, pero mostraría a los buenos peregrinos, si así lo deseaban, uno sobre el que había escuchado discutir a ciertas personas inteligentes de su vecindario: “El señor de la mansión en la región de Sussex de la que provengo tiene una plantación de dieciséis buenos robles, y están dispuestos de tal forma que hacen doce filas con cuatro árboles cada una. Una vez un hombre de gran sabiduría que iba de paso por esa zona, dijo que los dieciséis árboles podían haber sido plantados de manera que formaran quince filas rectas con cuatro árboles en cada una de ellas. ¿Podéis demostrarme cómo esto puede ser? Muchos han dudado de que sea posible de realizar.” La ilustración muestra una de las varias maneras de formar las doce filas. ¿Cómo podemos formar quince?
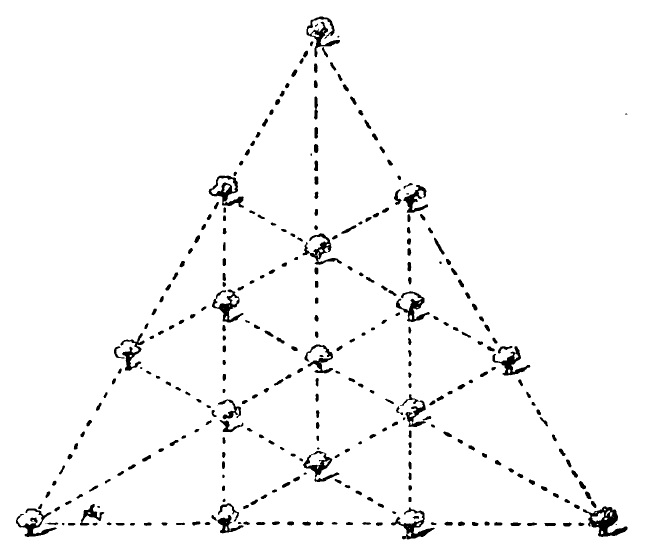
La solución a este acertijo es precisamente el diseño maximal de 16 puntos, con el que se forman 15 líneas rectas, con cuatro puntos en cada recta, que es un diseño simétrico hermoso y sugerente. Por lo tanto, r(16, 4) = 15.
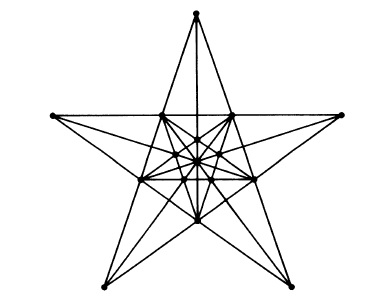
Mucho más difícil aún es el problema para líneas que contengan 5 árboles, es decir, k = 5. En la actualidad se conocen los valores de r(n, 5), para n entre 5 y 20, en concreto, los valores son 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 6, 6, 7, 9, 10 y 11. Para los primeros n (hasta 13) las estructuras maximales son triviales, una recta de cinco puntos, dos rectas de cinco puntos con un vértice común o un triángulo.
La solución maximal para n = 15 es la siguiente.
Como Martin Gardner comenta, la solución maximal simétrica para 16 puntos, formando filas con 4 puntos, que hemos visto arriba, recuerda a la estructura de flor de la Hoya carnosa o flor de cera, que se muestra en la siguiente imagen.

Bibliografía
1.- Miodrag S. Petkovic, Famous puzzles of Great Mathematicians, AMS, 2009.
2.- John Jackson, Rational Amusement for Winter Evenings, Longman, Hurst, Rees, Orme and Brown, 1821.
3.- Henry E. Dudeney, El misterio del muelle (Diversiones matemáticas III), Biblioteca Desafíos Matemáticos, RBA, 2008.
4.- Martin Gardner, Viajes en el tiempo y otras perplejidades matemáticas, Biblioteca Desafíos Matemáticos, RBA, 2007.
5.- Orchard-Planting Problem, Wolfram MathWorld.
6.- Stefan A. Burr, Branko Grunbaum, N. J. A. Sloane, The Orchand Problem, Geometriae Dedicata 2 (4), 1974, pp. 397-424.
7.- Ben Green, Terence Tao, On sets defining few ordinary lines, Discrete and Computational Geometry 50 (2), 2013, pp. 409–468.
8.- 3.- Henry E. Dudeney, Los acertijos de Canterbury, Biblioteca Desafíos Matemáticos, RBA, 2007.
9.- Tree Planting Problems, de Erich Friedman.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
