Preparando la charla “Jugando con las matemáticas” para el curso de verano de la UPV-EHU “Cultura con M de matemáticas”, me he encontrado con un curioso juego comercial llamado Vee-21, desarrollado por la empresa norteamericana de juegos de ingenio Kandon Enterprises, y que está relacionado con uno de los temas que me apasionan y sobre el que he hablado en esta conferencia, los poliominós.

Los poliominós fueron introducidos por el matemático e ingeniero norteamericano Solomon W. Golomb en una conferencia en el Harvard Mathematics Club en 1953, y en su posterior artículo “Checkers Boards and Polyominoes” publicado en la revista American Mathematical Monthtly. Pero serían descubiertos para el público general por el gran divulgador de las matemáticas Martin Gardner (1914-2010), en su columna de juegos matemáticos de Scientific American (1957). Al introducir los poliominós, Golomb abrió un fructífero campo para las matemáticas, las ciencias de la computación y la creación de juegos. Están relacionados con conceptos matemáticos como las teselaciones (o embaldosados), los patrones geométricos, los empaquetamientos o la medida (área), y de ellos han surgido infinidad de juegos de ingenio comerciales como el Katamino (el juego de los pentominoes), el Tetris, el Blokus, el Top-This, e infinidad de puzzles geométricos.

Un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro. Si unimos dos cuadrados se obtiene un dominó, si se juntan tres cuadrados se construye un triominó, o trominó, con cuatro cuadrados se tiene un tetraminó, con cinco un pentominó, y así se puede continuar para cualquier número de cuadrados.

Como vemos en la anterior imagen solo existen dos triominós, el I-triomino (por tener forma de I, o de palo) y el L-triominó (también llamado V-triominó, por su forma de L o V).

Pero volvamos al motivo que ha dado lugar a esta entrada, el juego Vee-21 (la V viene de los V-triominós y el 21 es la cantidad de fichas con forma de V-triominós). Como se muestra en la siguiente imagen, el juego consiste en un tablero 8 x 8, junto con 21 fichas de tres colores distintos (7 fichas de cada color), que son L-triominós, y una ficha negra cuadrada (de tamaño unidad, 1×1).

Este juego surge a partir de una demostración matemática. Norton Starr, profesor de matemáticas y ciencias de la computación del Amherst College de Massachusetts, fue quien sugirió a la empresa Kandon la realización de un juego basado en la demostración inductiva del problema del embaldosado por L-triominós de un tablero “deficiente” de 2ⁿ x 2ⁿ cuadrados (se elimina un cuadrado del tablero), que estaba enseñando a sus estudiantes en su curso de Matemáticas Discretas.

El problema de ingenio original que se plantearon los matemáticos, consistía en coger un tablero 8 x 8, del que se “quitaba” uno de los cuadrados, y ver si se podía recubrir con piezas con forma de L-triominó, exactamente 21 piezas (puesto que 64 – 1 = 3 x 21). En la siguiente imagen vemos un tablero 8 x 8 al que se le ha eliminado un cuadrado, pintado de blanco, y una de las fichas de L-triominó con las que hay que cubrir este tablero deficiente.

Pero en el juego Vee-21 los L-triominós tienen además color, tres colores distintos y 7 fichas de cada color. Y las reglas del juego se derivan además de otro resultado matemático, el teorema de los cuatro colores. Este resultado dice que “bastan cuatro colores para colorear un mapa geopolítico plano, sin que dos países con frontera común tengan el mismo color” (para más información, el artículo de Marta Macho ¿Cuatro colores son suficientes?).

Por lo tanto, las reglas del Vee-21, que son una combinación del problema del embaldosado de un tablero deficiente con L-triominós y el teorema de los cuatro colores, son las siguientes. En primer lugar, se coloca la pieza cuadrada unidad de color negro o blanco, dependiendo de la versión, en uno de los cuadrados del tablero 8 x 8 del juego, y entonces el reto consiste en colocar las 21 fichas con forma de L-triominó de manera que cubran completamente el tablero deficiente que ha quedado (es decir, teselar el tablero deficiente con los L-triominós), pero con una condición extra, que las fichas del mismo color no se puedan tocar entre sí, salvo quizás por los vértices, como en el teorema de los cuatro colores.

La empresa Kandon Enterprises ha completado el juego Vee-21 con una serie de retos, puzzles y diseños geométricos para realizar en este tablero con los 21 triominós de colores y el cuadrado unidad.

Pero vayamos al problema matemático del embaldosado de tableros deficientes y a la demostración por inducción dada por Solomon W. Golomb para el caso particular de las potencias de 2.

El ajedrez es un juego que ha apasionado desde siempre a los matemáticos, que se han planteado interesantes problemas relacionados con el mismo, como el problema de las rutas de un caballo sobre el tablero de ajedrez, al que dedicaron su tiempo grandes matemáticos como el francés Abraham de Moivre (1667-1754) o el suizo Leonhard Euler (1707-1783), a este último también le interesó el problema de calcular el número de formas de colocar ocho torres en un tablero, o el problema de las ocho reinas que interesaría al “príncipe de las matemáticas”, Carl Friedrich Gauss (1777-1855).

Pero también se plantearon otra serie de problemas de ingenio sobre un tablero de ajedrez, en particular relacionados con la teselación del mismo mediante diferentes poliominós. El más sencillo es el clásico problema de recubrir con fichas “dominó” (es decir, formadas con dos cuadrados) un tablero de ajedrez “mutilado”, del que se han eliminado dos cuadrados, como los que se muestran en la siguiente imagen.

El siguiente paso sería el embaldosado del tablero de ajedrez mediante triominós. Así, Solomon W. Golomb se planteó el problema de cubrir un tablero de ajedrez deficiente, es decir, al que se había eliminado un cuadrado cualquiera, mediante 21 L-triominós. Aunque como suele ser habitual en matemáticas, Golomb se planteó el problema de forma más general. Consideró cualquier tablero de tamaño m x m, es decir, de m cuadrados de lado, al que le quitó un cuadrado, quedándole m²-1 cuadrados, y le llamó un “tablero deficiente” si m²-1 era divisible por 3. Luego los lados de esos tableros deficientes eran los elementos de la sucesión 2, 4, 5, 7, 8, 10, 11, 13, 14,… y el problema quedó planteado así.

Problema: ¿Qué tableros deficientes pueden ser recubiertos con L-triominós?

El propio Golomb ofreció una demostración por inducción para tableros deficientes de lado 2ⁿ, que es un bonito ejemplo para ilustrar este tipo de demostraciones.

Pero expliquemos a las personas que no estén familiarizadas con el concepto de “demostración por inducción” que significa esta expresión. Imaginemos que deseamos demostrar una propiedad o proposición que depende de un parámetro n. La demostración por inducción se divide en dos partes:

i) la demostración de la propiedad para el primer número natural para el que se verifica, normalmente n = 0 ó 1;

ii) demostrar que si la propiedad se satisface para un número k-1, se verificará para el número k;

Entonces, por inducción, la propiedad se satisface para todo número n.

Al igual que hizo Solomon W. Golomb, a continuación demostremos la propiedad “todo tablero deficiente de lado 2ⁿ se puede embaldosar con L-triominós”.

Antes de nada, deberíamos plantearnos la cuestión de si los tableros de lado 2ⁿ son deficientes, es decir, si 2ⁿ-1 es múltiplo de 3. Este es un pequeño reto que dejo para las personas que están leyendo esta entrada del Cuaderno de Cultura Científica.

– Paso 1. La propiedad se cumple para n = 1. Claramente, un tablero 2 x 2 al que se le quita un cuadrado puede ser cubierto con un único L-triominó.

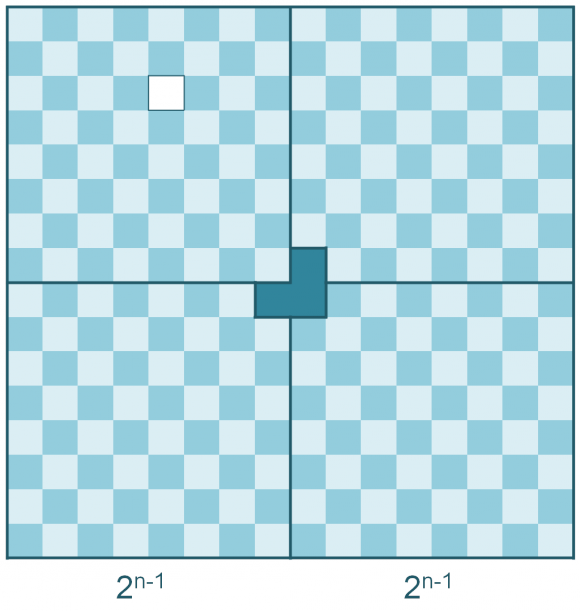
– Paso 2. Supongamos que la propiedad se cumple para n-1, es decir, para los tableros deficientes de lado 2^n-1 y demostremos que entonces se cumplirá también para cualquier tablero deficiente de lado 2ⁿ. Para ello vamos a utilizar la técnica del “divide y vencerás”.

Para empezar, se divide el tablero 2ⁿ x 2ⁿ en cuatro tableros de medida 2^n-1 x 2^n-1, como se muestra en la imagen. Como el tablero original 2ⁿ x 2ⁿ es deficiente, el cuadrado blanco (el eliminado) quedará en uno de los cuatro cuadrados menores 2^n-1 x 2^n-1, que será deficiente también, y además, si colocamos un L-triominó en el centro del tablero, como se muestra en la imagen, entonces los otros tres tableros 2^n-1 x 2^n-1 también serán deficientes. Como, por hipótesis, la propiedad se cumple para n-1, estos cuatro tableros deficientes 2^n-1 x 2^n-1 se pueden embaldosar con L-triominós, y por tanto, el tablero deficiente original, de lado 2ⁿ, también.

En consecuencia, la propiedad “todo tablero deficiente de lado 2ⁿ se puede embaldosar con L-triominós” se cumple para todos los números n.

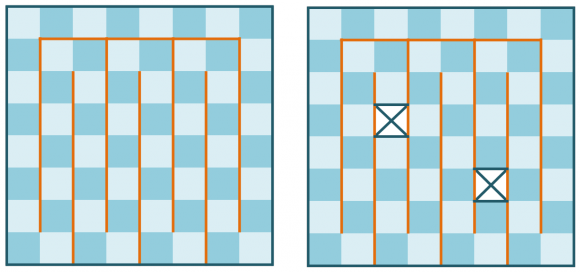
Volviendo al problema de teselar un tablero deficiente de lado m, ¿tendrá solución para m = 5? La respuesta es negativa, ya que solo podrá ser recubierto mediante L-triominós, dependiendo de cuál sea el cuadrado eliminado del tablero. Por ejemplo, si el cuadrado eliminado es el central, como se muestra en la siguiente imagen, el tablero deficiente puede ser cubierto por rectángulos de dimensión 2 x 3, pero cada uno de estos se construye con dos triominós, en consecuencia, la respuesta es afirmativa en este caso. Sin embargo, si se quita el cuadrado que está en la segunda fila y la tercera columna, como se muestra en la siguiente imagen, el tablero resultante no puede ser cubierto por L-triominós. La explicación es sencilla. Para cubrir el cuadrado con el número 3, habría que poner un L-triominó como el que se muestra en la imagen y que ocupa los cuadrados 3-4-8 (respectivamente, uno simétrico, que ocupe los cuadrados 2-3-7), pero en ese caso ningún L-triominó podría cubrir el cuadrado 9 (respectivamente, el cuadrado 1).

¿Qué ocurre para m = 7? En este caso, la respuesta es afirmativa. Martin Gardner en su artículo “L-tromino Tiling of Mutilated Chessboards” (2009) reproduce la demostración que Golomb le envió personalmente, pero que no está publicada. Esta demostración se basa en los tres diagramas de la imagen siguiente, que embaldosan los tableros deficientes de lado 7 mediante rectángulos 2 x 3 (que trivialmente pueden cubrirse con dos L-triominós) y solitarios L-triominós, junto con un cuadrado 2 x 2, que es el que contiene al cuadrado eliminado. Estos diagramas recorren, por simetría, todas las posibilidades.

Gardner nos plantea buscar embaldosados que maximicen el número de losetas rectangulares 2 x 3, en los casos derivados del tercer diagrama.

El argumento por inducción de Golomb empezando en tableros deficientes de lado 7 nos llevaría a demostrar que todos los tableros deficientes de lado 2ⁿ7, por ejemplo, aquellos de lado 14 o 28, se pueden embaldosar mediante L-triominós.

¿Qué ocurre para el tablero deficiente de lado 10? En este caso, no se puede utilizar el argumento inductivo mediante la duplicación del tablero deficiente de lado 5, puesto que precisamente para este no se satisface la propiedad. Sin embargo, se puede demostrar mediante otro tipo de razonamiento, como nos muestra Gardner en su artículo de 2009.

De nuevo el argumento inductivo nos llevaría a resolver el problema para tableros deficientes de lados igual a 20, 30, 40, etc. Y así podríamos seguir encontrando casos particulares, o familias, de tableros deficientes que pueden ser teselados con L-triominós, sin embargo, la cuestión del embaldosado de tableros deficientes mediante L-triominós fue resuelta completamente en el año 1986 por I. P. Chu y R. Johnsonbaugh en su artículo “Tiling deficient boards with trominoes” (1986).

Teorema (I. P. Chu, R. Johnsonbaugh): Todo tablero deficiente m x m se puede recubrir con L-triominós, salvo para m = 5.

Pero Chu y Johnsonbaugh no solo resolvieron el problema de los tableros (cuadrados) deficientes, sino que en su siguiente artículo “Tiling boards with trominoes” (1985-86) resolvieron tanto el caso de los tableros rectangulares, como el de los tableros rectangulares deficientes.

Teorema (I. P. Chu, R. Johnsonbaugh): Un rectángulo m x n, con 2 ≤ m ≤ n y para el que 3 divide a mn, puede ser embaldosado con L-triominós excepto para rectángulos 3 x (2k+1), para k ≥ 1.

Teorema (I. P. Chu, R. Johnsonbaugh): Un rectángulo deficiente m x n (3 debe dividir a mn-1), con 2 ≤ m ≤ n, puede ser embaldosado con L-triominós si se satisface: i) si m = 2, entonces n = 2; ii) m  5.

Este es un tópico en el que se sigue investigando hoy en día, pero no es nuestra intención mostrar aquí el camino que ha seguido dicha investigación.

Pero regresemos a la cuestión del embaldosado mediante L-triominós de colores que aparece en el juego Vee-21. Como vimos más arriba, pudimos resolver el problema 1 utilizando los L-triominós de colores del Vee-21 sin que las fichas de color azul, rojo y verde se tocaran entre sí, salvo por los vértices. Una cuestión que nos podríamos plantear es si dado un embaldosado en el que no hemos tenido en cuenta los colores de las losetas con forma de L-triominó, se podrían colorear a posteriori para que cumplieran la condición de que las fichas del mismo color no se toquen entre sí, con la excepción de los vértices. Por ejemplo, dado el embaldosado concreto que hemos obtenido mediante el método de inducción del tablero deficiente del problema 1, ¿se podrán colorear los L-triominós (7 de cada uno de los tres colores) para que satisfagan la condición sobre el color? La respuesta es que no. Demostrémoslo.

En la página de la empresa Kandon han planteado otra cuestión más relacionada con los colores, el problema de los tres colores: ¿será posible embaldosar el tablero 8 x 8 con las 21 piezas con forma de L-triominó y el cuadrado unidad blanco (o negro), de forma que las piezas del mismo color no estén en contacto ni siquiera por los vértices? En 2004 recibieron una respuesta del Profesor Andris Cibulis y su estudiante, Marina Klimova, de la University of Latvia, en la que probaban que la separación total, de los tres colores, es imposible. Además, Kandon ha planteado a los visitantes de la página que encontrasen soluciones en las que uno de los colores sí puede estar en contacto por los vértices, pero los otros dos no. Aquí os dejo tres de las siete respuestas que les han enviado (para más información, página de Kandon sobre el problema de los tres colores).

Para terminar esta entrada del Cuaderno de Cultura Científica, vamos a resolver los problemas 2 y 3 planteados más arriba. El problema 2 es un clásico. La respuesta es que no se pueden cubrir los 62 cuadrados de un tablero de ajedrez al que se le han quitado dos cuadrados de esquinas opuestas, con 31 “dominós”. El motivo es que cada “domino” cubre un cuadrado blanco y uno negro, luego los 31 dominós cubrirán tantos cuadrados blancos como negros, sin embargo, un tablero de ajedrez al que se le han quitado dos esquinas opuestas tiene más cuadrados de un color que del otro (si se han quitado las esquinas blancas quedarán 30 cuadrados blancos y 32 negros, y en el caso de las esquinas negras al revés).

Respecto al problema 3, de nuevo Martin Gardner nos enseñó en su libro “El ahorcamiento inesperado y otros entretenimientos matemáticos” una preciosa demostración de Ralph Gomory de que este problema sí tiene solución, independientemente de cuáles sean los dos cuadrados quitados (podemos suponer, por lo anteriormente comentado, que uno es blanco y el otro negro). La demostración se basa en el trazado del camino cerrado sobre el tablero de ajedrez que aparece en la siguiente imagen, que claramente está formado por una sucesión de cuadrados alternativamente blancos y negros. Luego si se eliminan dos cuadrados de distintos colores de ese camino, que es lo que hacemos en nuestro problema al eliminar dos cuadrados de colores distintos del tablero, entonces cada uno de los dos caminos que unen los dos cuadrados eliminados está formado por un número par de cuadrados de colores alternos, luego se pueden recubrir con dominós.

Bibliografía

1.- Norton Starr, The Tromino Puzzle (Tiling a Deficient Checkerboard with L-Trominoes).

2.- Kandon Enterprises

3.- Solomon W. Golomb, Polyominoes, Princeton University Press, 1994.

4.- Marta Macho, ¿Cuatro colores son suficientes?, Un paseo por la geometría, UPV-EHU, 2005; versión on-line en divulgamat

5.- George E. Martin, Polyominoes, a guide to puzzles and problems in tiling, The Mathematical Association of America, 1996.

6.- Martin Gardner, L-tromino Tiling of Mutilated Chessboards, The College Mathematics Journal 40, n. 3, 2009, p. 162-168.

7.- I. P. Chu, R. Johnsonbaugh, Tiling deficient boards with trominoes, Mathematics Magazine 59, 1986, p. 34-40.

8.- I. P. Chu, R. Johnsonbaugh, Tiling boards with trominoes, J. Rec. Math. 18, 1985–86, p. 188–193.

9.- Kandon Enterprises, el problema de los tres colores

10.- Martin Gardner, El ahorcamiento inesperado y otros entretenimientos matemáticos, Alianza editorial, 1969.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Esta anotación participa en la XI Edición del Carnaval de Humanidades cuyo blog anfitrión es SCIENTIA