Para celebrar que esta es mi entrada número doscientos en la sección Matemoción del Cuaderno de Cultura Científica, voy a recurrir a un clásico de la divulgación de las matemáticas, la leyenda del origen del ajedrez.
La relación entre ajedrez y matemáticas ha sido siempre muy fructífera. Problemas clásicos como el recorrido del caballo sobre el tablero de ajedrez o el problema de las ocho reinas, entre otros, fueron estudiados por grandes matemáticos como Carl F. Gauss, Leonhard Euler, Abraham de Moivre o Adrien-Marie Legendre. Así mismo, muchos matemáticos recreativos como Lewis Carroll, W. W. Rouse Ball, Henry E. Dudeney, Sam Loyd, Édouard Lucas, Raymond Smullyan o Martin Gardner, se apasionaron con este juego, incluso fueron grandes jugadores, e inventaron interesantes rompecabezas matemáticos y juegos de ingenio sobre el tablero de ajedrez.
Realmente, se desconoce cuál es el origen del ajedrez. Sabemos que fue introducido en Europa por los árabes, que lo habían aprendido de los persas, pero a ellos les pudo llegar tanto de la India, como de China. Su origen, tan remoto en el tiempo, ha propiciado que existan muchas leyendas, una de ellas relacionada con las matemáticas.
En esta, se atribuye su invención al brahmán hindú Sissa ben Dahir, que presentó el juego al rey Shirham de la India. Este, en agradecimiento, quiso premiar al brahmán y le pidió que fuese él mismo quien escogiera la recompensa por tan maravillosa invención. El brahmán solicitó que se le pagase en trigo. Un grano de trigo en pago por la primera casilla del tablero de ajedrez, dos granos por la segunda casilla, 4 por la tercera, 8 por la cuarta, … y así sucesivamente, doblando en cada casilla la cantidad de trigo de la casilla anterior. Al monarca le sorprendió la modestia de semejante petición, por lo que dio orden a sus ministros de que le fuera inmediatamente pagada esa cantidad de trigo.
Días más tarde, el rey enfadado al enterarse de que el brahmán aún no había sido pagado, mandó llamar a sus ministros. Estos le informaron de que había un problema… ¡¡El rey no tenía tal cantidad de trigo!!

La cuestión es entonces la siguiente:
¿Cuánto trigo había solicitado exactamente el brahmán?
Veámoslo. Serían, en la primera casilla 1, en la segunda el doble 2, en la tercera el doble 22 = 4, es decir, es la suma de las potencias de 2, desde la potencia 0 (2 elevado a 0 es 1) hasta la 63 (hay 64 casillas y hemos empezado por 20), es decir,
1 + 2 + 22 + 23 + … + 263 (granos de trigo).
Como se observa, la suma de una progresión geométrica, de factor de progresión 2. En matemáticas tenemos una sencilla fórmula para calcular esta suma, que nos dice que esta suma es igual a
264 – 1 = 18.446.744.073.709.551.615,
es decir, más de 18 trillones de granos de trigo.
Pero la cuestión es saber si dicha cantidad de trigo es realmente grande o no, y en caso de serlo, cuánto de grande puede ser.
Si tomamos como cierta la estimación de que hay 15 millones de granos de trigo por metro cúbico, la cantidad solicitada por el brahmán equivale aproximadamente a un billón 230 mil millones (1.230.000.000.000) de metros cúbicos. Si tuviésemos que almacenarla en un silo, este podría tener, por ejemplo, uno de los siguientes tamaños:
i) un silo con una base que fuese igual a la superficie de todo el territorio histórico del País Vasco (que incluye las siete provincias o herrialdes, a saber, Bizkaia, Gipuzkoa, Araba y Navarra, en España, y Lapurdi, Zuberoa y la Baja Navarra, en Francia), que es de 20.664 km2, y que tendría ¡¡¡una altura de casi 60 metros!!!;
ii) o un silo que tuviera una base con la superficie de toda la Península Ibérica (580.000 km2) y que tendría una altura de más de 2 metros; en conclusión, un silo enorme.

Pero sigamos pensando un poco en el trigo que el rey Shirham tenía que entregar al brahmán y preguntémonos:
¿Había alguna posibilidad de que el rey pudiese conseguir tal cantidad de trigo?
Según la base de datos (FAOSTAT) de la FAO, es decir, la Organización de las Naciones Unidas para la Alimentación y la Agricultura, la producción mundial de trigo en 2017 (último año con datos recogidos) fue de 771.718.589 toneladas de trigo. Luego, para poder calcular las toneladas que tenía que pagar el rey Shirham, necesitamos saber cuánto pesa el trigo. Ese dato nos lo da lo que se conoce como peso específico, la cantidad de kilos por hectolitro (0,1 metros cúbicos), del trigo. Aunque existen variaciones (en función de los tipos de trigo y otros factores), podríamos fijar una cantidad aproximada de 800 kilos de trigo por metro cúbico. Por lo tanto, los, más o menos, un billón 230 mil millones (1.230.000.000.000) de metros cúbicos, pesarían del orden de 984 mil millones (984.000.000.000) de toneladas.
Por lo tanto, si la producción de 2017 era de unos 780 millones de toneladas, se necesitarían unos 1.250 años de producción de trigo (del tamaño de la producción de 2017) en todo el mundo para pagar la deuda.
Pero está claro que la producción en aquel tiempo era muchísimo menor. Si tomamos como referencia la producción mundial de trigo en el siglo XIX, que era menor que 100 millones de toneladas, pero en cualquier caso mucho mayor que en la época de la leyenda, se necesitarían, como mínimo, unos 10.000 años con toda la producción mundial para cubrir la demanda de Sissa ben Dahir. Si tenemos en cuenta que el ser humano empezó a cultivar el trigo, más o menos, hacia el 9.500 a.c., y que entonces la producción era mínima, es posible que toda la producción de trigo de la historia no fuese suficiente para pagar el precio de la invención del ajedrez.

Sorprendente, ¿no? Pero démosle una vuelta de tuerca más a la historia:
¿Cuánto tiempo tardaría uno de los sirvientes del rey Shirham en contar la deuda de granos de trigo (suponiendo claro que los tuviese y que contase a una velocidad de un grano por segundo)?
El tiempo que se tarda es de nuevo más de 18 trillones de segundos. Teniendo en cuenta que hay 31.557.600 segundos en un año, nuestra cantidad es más de 584 mil millones de años. Los físicos que estudian el origen del universo (el Big Bang) estiman que este se produjo hace 15 mil millones de años y que, según la teoría vigente sobre la evolución del universo, puede que este dure todavía entre 10 y 15 mil millones de años… luego realmente no existe el tiempo para poder contar directamente, una sola persona, esa cantidad de granos de trigo… Bueno, toda la población mundial actual, unos 7.800 millones de personas, tardaríamos del orden de 75 años entre todos.

Como decíamos al principio de esta entrada, existen muchos problemas matemáticos y juegos de ingenio que tienen como base el ajedrez, ya sea solo el tablero, o también las piezas del juego. Para terminar esta entrada me gustaría recordar unos pocos de estos juegos para que puedan divertirse “jugando” las personas que así lo deseen.
Problema 1: Dado un tablero de ajedrez, 8 x 8, del que eliminamos dos casillas opuestas de las esquinas (por ejemplo, pongamos en ellas dos peones), ¿es posible recubrir este tablero con fichas de dominó (suponiendo que estas fichas tienen el tamaño de dos casillas)?
Este problema es un clásico que aparece en muchos libros de pasatiempos matemáticos. Es interesante como ejemplo de problema que no tiene solución y hay que buscar un razonamiento que explique el motivo por el cual no existe tal solución.
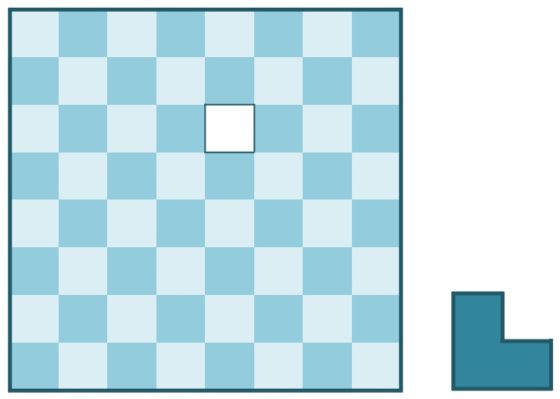
Problema 2: Si se consideran ahora triominós, que son fichas con tres casillas, pero en forma de L. No puede rellenarse el tablero 8 x 8 con estas fichas, puesto que 64 no es divisible por 3. Sin embargo, si eliminamos una casilla del tablero (por ejemplo, poniendo un peón), ¿será posible recubrir este tablero?
Este es un interesante problema sobre el que podéis leer en la entrada del Cuaderno de Cultura Científica titulada Embaldosando con L-triominós (un ejemplo de demostración por inducción).
Problema 3 (el recorrido del caballo): Utilizando la pieza del caballo, con su particular movimiento en el ajedrez, realizar un recorrido por todas las casillas del tablero, sin repetir casilla.
Este es un problema clásico. Puede leerse sobre el mismo en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos, así como en muchos otros textos. Y otro problema clásico y estudiado por grandes matemáticos es el siguiente.
Problema 4 (las ocho reinas en el tablero de ajedrez): Colocar ocho reinas en el tablero de ajedrez de manera que ninguna de las reinas se vea amenazada por las otras siete.
Puede leerse sobre este problema en el libro Recreaciones Matemáticas, de Édouard Lucas.


Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).
3.- Antonio J. Durán (idea), Vida de los números, textos de Antonio J. Durán, Georges Ifrah, Alberto Manguel, T ediciones, 2006.
4.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
5.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Víctor Callirgos
Gracias
Santiago Jose Tonsich
En Sudamérica, los indios guaraníes nombraron al colofón de las partidas, le sacaron el ¡jaque! y dejaron el MATE
Alejandro Melchor
Sí, todo ello es conocido por nosotros los ajedrecistas; el problema de las 8 Damas es relativamente fácil, con papel y lápiz; el de el caballo que pase por todas las casillas, es mas difícil y aunque te acerques a las 55 casillas, siempre te quedas sin espacio para las 8-10 restantes (!), y eso que hay varios cientos de soluciones posibles, y que con un cierto «orden» metodológico en el recorrido te acercas casi al final.
Joan R. Malonda
Esta leyenda del ajedrez la uso con mis alumnos de 10-12 años para ilustrarlos sobre el alcance de la notación científica, que comprende las potencias de diez.
Además les hago partícipes de la historia preguntándoles, antes de entrar en más detalles sobre la abrumadora cantidad de trigo necesario, si creían que la generosidad del rey había sido insultada por Sissa Ben Dahir, : «¿Vosotros habríais pedido al rey otra cosa? ¿Creéis que el brahmán se burlaba del rey, o que simplemente no deseaba más que un simple agradecimiento?» La respuesta mayoritaria es del estilo «el brahmán es tonto: ¡mira que pedir un puñado de trigo!». Ya los tengo donde yo quería.
Empezamos la demostración. Para ello iremos cambiando de unidad de medida según vayamos cubriendo las casillas de trigo. ¿Per qué unidades de medida les son familiares? Pues no necesariamente del S.I. Profesor y alumnos vamos declamando desde el principio algo así:
1ª: un grano de trigo
2ª: dos granos de trigo
3ª: cuatro granos de trigo
4ª: ocho granos de trigo, que pesan más o menos 1g.
5ª: 2g de trigo
6ª: 4g de trigo…
… (se sigue con los alumnos la serie en gramos)
13ª: 512g de trigo, es decir, más o menos medio kg de trigo
14ª: 1kg de trigo
15ª: 2kg de trigo
16ª: 4kg de trigo
… (se sigue con los alumnos la serie en kg)
24ª: 1024 kg, es decir, más o menos una Tm
25ª: dos toneladas de trigo…
…28ª: 16 Tm, es decir, un camión de trigo
29ª: dos caminones de trigo…
…34ª: 64 caminones de trigo, es decir, un tren
35ª: dos trenes de trigo…
…42ª: 256 trenes de trigo, es decir, un buque carguero transoceánico (ya os habréis percatado de que la terminología ayuda al asombro)
43ª: dos transoceánicos de trigo…
…50ª: 256 buques transoceánicos de trigo, es decir una producción anual de toda Europa
51ª: dos producciones anuales de trigo de toda Europa…
…54ª: la producción de todo el mundo de un año!
55ª: ¡¡la producción mundial de trigo de dos años!!
¡¡¡ Y aun vamos por 2 elevado a 54!! ¿Necesitaremos colonizar todo el
Sistema Solar para llegar a las 64 casillas?
Está claro que no he comprobado las equivalencias de los cambios de unidades, pero seguro que los valores estimados son más que verosímiles.
Esta actividad con los alumnos acaba repitiéndoles las pregunta inicial: «¿Quién era el más listillo de todos: el rey, el brahmán o vosotros?»
El tema de potencias y notación científica ha comenzado.
Ajedrez y matemáticas: el problema de Guarini — Cuaderno de Cultura Científica
[…] mi anterior entrada en el Cuaderno de Cultura Científica, A vueltas con el origen del ajedrez, mencionamos la fructífera relación que ha existido, y existe, entre las matemáticas y el […]
Ajedrez y matemáticas: el problema de Guarini
[…] mi anterior entrada en el Cuaderno de Cultura Científica, A vueltas con el origen del ajedrez, mencionamos la fructífera relación que ha existido, y existe, entre las matemáticas y el […]
Ajedrez y matemáticas: el problema de Guarini
[…] mi anterior entrada en el Cuaderno de Cultura Científica, A vueltas con el origen del ajedrez, mencionamos la fructífera relación que ha existido, y existe, entre las matemáticas y el […]
El problema del recorrido del caballo en el tablero de ajedrez — Cuaderno de Cultura Científica
[…] ya mencionamos en la entrada del Cuaderno de Cultura Científica titulada A vueltas con el origen del ajedrez, la relación entre ajedrez y matemáticas ha sido siempre muy […]