En mi anterior entrada en el Cuaderno de Cultura Científica, A vueltas con el origen del ajedrez, mencionamos la fructífera relación que ha existido, y existe, entre las matemáticas y el ajedrez.

Muchos rompecabezas matemáticos y juegos de ingenio tienen al tablero y las piezas del ajedrez como elementos principales. En esta entrada vamos a prestar atención a algunos problemas que utilizan la pieza del caballo, con su movimiento característico en forma de L, moviéndose en todo el tablero o en parte del mismo. Uno de los principales problemas de este tipo es “el recorrido del caballo en el tablero de ajedrez”, que interesó a grandes matemáticos como Abraham de Moivre, Pierre de Montmort, Leonhard Euler o Adrien-Marie Legendre, y sobre el que podéis leer, por ejemplo, en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos (RBA, 2015). Sin embargo, en esta entrada vamos a interesarnos por el problema de Guarini y otros relacionados.

El problema de Guarini pertenece a una familia de juegos solitarios que consisten en intercambiar la posición de dos grupos distintos de fichas, normalmente de diferente color, blancas y negras, ya sea mediante el desplazamiento de las mismas –como Todas cambian, La estrella de ocho puntas o el Kono de cinco– o permitiéndose además saltar sobre las fichas contrarias –como El salto de la rana o El puzzle dieciséis inglés (sobre los que se puede leer en el artículo El salto de la rana, y familia), aunque en este caso las fichas son los caballos blancos y negros del ajedrez.

Antes de adentrarnos en el problema de Guarini os propongo jugar a dos versiones de un solitario de esta familia de juegos de intercambio de fichas sobre cierto tablero, el sencillo juego Todas cambian. En ambas versiones se juega con tres fichas (aunque puede generalizarse a un número mayor) de cada color, blancas y negras, sobre los tableros y con las posiciones iniciales que se muestran en la imagen.

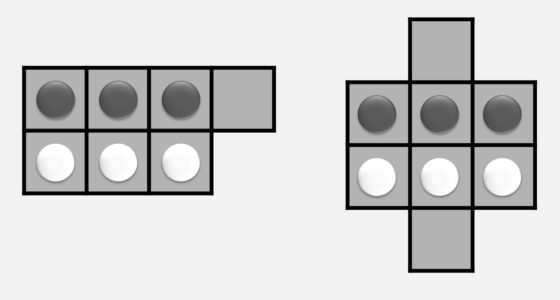
Las reglas del solitario Todas cambian son las siguientes:

i) las fichas se mueven de una en una, y cada una puede desplazarse a una posición adyacente que esté libre;

ii) cada desplazamiento puede ser realizado en horizontal (a izquierda o derecha), en vertical (hacia arriba o abajo) o en diagonal;

iii) el objetivo es intercambiar la posición de las fichas negras y blancas en el menor número de movimientos posible.

Estos son juegos ideales para pasar un buen rato, y su solución es lo que podríamos llamar una demostración constructiva. Sabemos que existe solución al reto porque la encontramos explícitamente, la construimos.

Por otra parte, el procedimiento para encontrar la solución es el básico método del ensayo y error, que consiste en realizar repetidos y variados intentos, en muchas ocasiones sin una regla aparente, hasta alcanzar el éxito. El problema de este procedimiento es que se trata de una búsqueda aleatoria, que no garantiza encontrar la solución, salvo que sea posible explorar todas las opciones, y aunque se encuentre la solución, no genera una técnica útil para utilizar con otros problemas, ni explica el motivo de la misma.

Antes de seguir leyendo, os animo a jugar a estos solitarios y a buscar vuestras soluciones a los mismos.

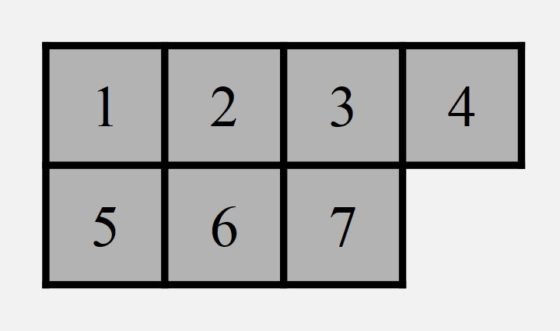
No es difícil de demostrar que la solución al primer juego puede alcanzarse en siete movimientos. Si numeramos los cuadrados de la primera fila como 1, 2, 3, 4 y de la segunda 5, 6, 7, y describimos cada movimiento como un par de números, la casilla origen de la ficha y la de llegada, entonces, la solución se puede expresar: (7,4), (2,7), (5,2), (1,5), (6,1), (3,6), (4,3). En realidad, no necesitamos tanta información, nos bastará con mencionar cuál es el hueco sin ficha, a partir del 4 inicial, esto es, 7 – 2 – 5 – 1 – 6 – 3 – 4.

En diez movimientos se pueden intercambiar las fichas en el segundo tablero, aunque si se añade la condición extra de mover las fichas blancas y negras alternativamente, entonces serán necesarios un mínimo de doce. Es aconsejable mantener un registro de los movimientos realizados para comprobar que la solución ha sido correcta y contar el número de pasos.

Pero vayamos ya al pasatiempo relacionado con el ajedrez, el problema de Guarini. Este juego nos sirve además para ilustrar un procedimiento muy útil en el trabajo matemático, como es cambiar el punto de vista. Si el problema que estamos intentando resolver es complejo o la técnica que estamos utilizando no parece la apropiada, transformar el problema original en otro más sencillo o para el que conozcamos algún procedimiento que permita resolverlo, puede ser una estrategia exitosa.

El Problema de Guarini, de intercambio de caballos en un tablero de ajedrez de tamaño 3 x 3, aparece como el problema 42 en un manuscrito de 1512 del impresor, tipógrafo y arquitecto italiano Paolo Guarini di Forli (1464-1520), y dice lo siguiente:

“Dos caballos blancos y dos caballos negros están colocados en las cuatro esquinas de un tablero cuadrado de nueve casillas; se pide hacer pasar, según las reglas, los caballos blancos al lugar que ocupan los caballos negros, e inversamente, sin salirse del cuadrado”.

Aunque es algo muy conocido, vamos a recordar primero cómo es el movimiento del caballo en el ajedrez. Esta pieza realiza un salto o movimiento en forma de L –dos casillas hacia delante y una a un lado– como los que se muestran en la siguiente imagen.

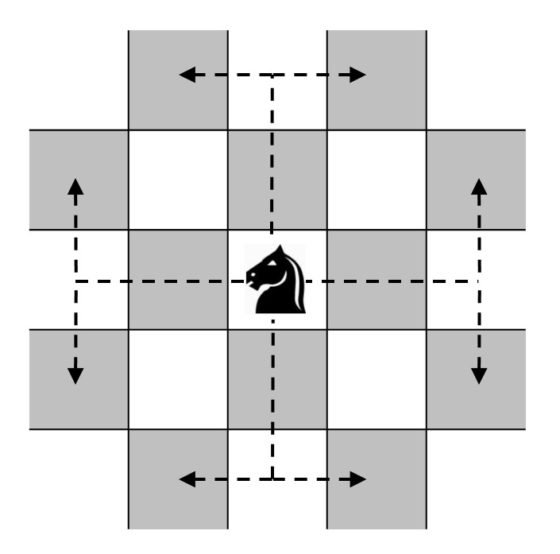
En la siguiente imagen se muestra el tablero del problema de Guarini y su posición inicial.

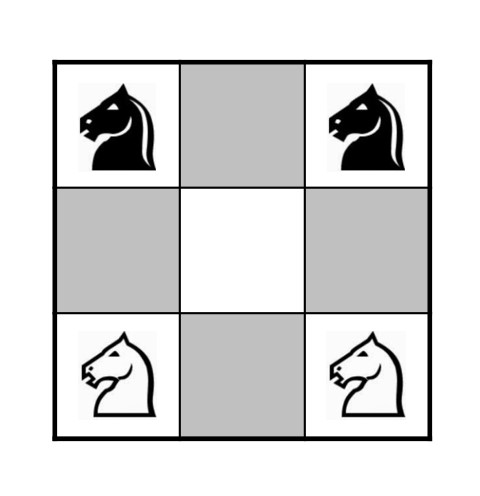
Este solitario ya aparecía en la recopilación de problemas de ajedrez y juegos de tablero del siglo XV, Civis Bononiae (Ciudadano de Bolonia), aunque realmente esa fue solo su primera aparición en Europa, puesto que había sido incluido, unos siglos antes, en el primer manuscrito árabe sobre ajedrez kitab ash-shatranj (hacia el año 840) del jugador y teórico árabe del shatranj, una forma antigua de ajedrez, al-Adli.

Un primer acercamiento al problema de resolver este desafío, consiste en transformarlo en el llamado Juego de la estrella de ocho puntas, que realmente no es más que el grafo asociado al Problema de Guarini.

La idea es representar mediante un esquema sencillo y útil los posibles movimientos del caballo en el tablero de ajedrez 3 x 3. Las casillas del tablero (que numeramos del 1 al 9 como en la imagen de abajo) se van a representar como puntos o círculos y los movimientos del caballo, de una casilla del tablero a otra, se representan mediante líneas que unen esos círculos (salvo el cuadrado central que es un punto aislado).

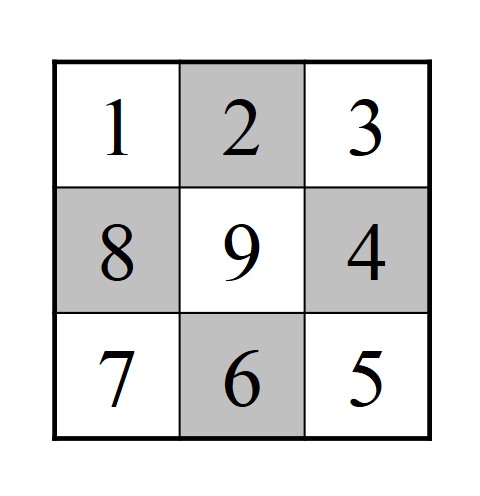
Así, se obtiene una estrella de ocho puntas y el Problema de Guarini de cambio de posición de caballos se transforma en el solitario que consiste en intercambiar la posición de las fichas blancas y negras (que son los dos caballos blancos y los dos negros), siendo los posibles movimientos de las fichas los desplazamientos a lo largo de las líneas de la estrella.

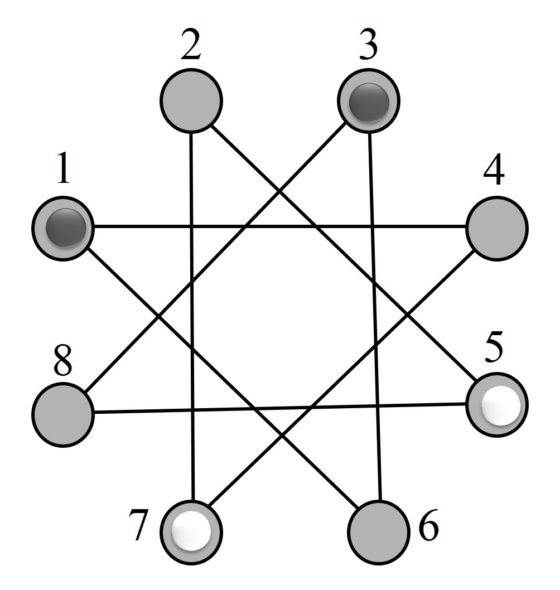
Esta presentación más moderna y sencilla del problema de Guarini, al igual que el problema original sobre el pequeño tablero de ajedrez, puede intentar solucionarse con el habitual método de ensayo y error. Sin embargo, antes de abalanzarnos sobre el mismo, podemos analizarlo un poco más y descubrir que realmente es un problema más simple de lo que aparenta, si se enfoca convenientemente.

Si nos fijamos en las líneas que unen los círculos, observaremos que realmente constituyen un ciclo circular cerrado. Por lo tanto, podemos desenrollar la estrella y transformarla en el circuito circular de la imagen, siendo la solución del solitario tan simple como desplazar las fichas en uno de los sentidos, por ejemplo, en el de las agujas del reloj.

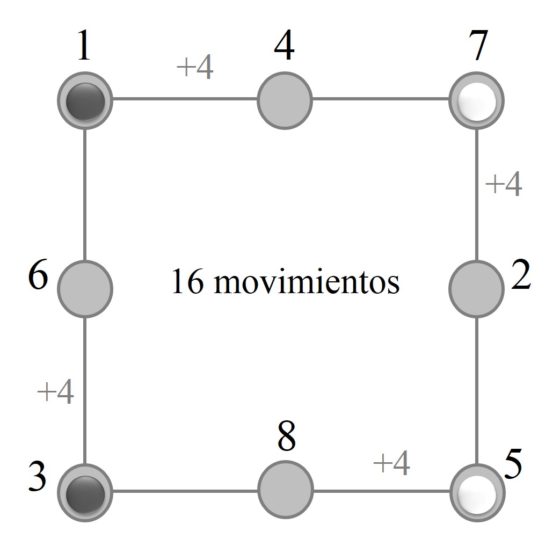
La solución consta de dieciséis movimientos, que consisten en desplazar cada una de las fichas cuatro posiciones en el sentido de las agujas del reloj. Esta solución llevada al problema de Guarini original describe en un cierto movimiento simétrico de los caballos alrededor del cuadrado central. El matemático recreativo británico Henry E. Dudeney (1857-1930) llamaba al anterior método de resolución, el “método de los botones y la cuerda”.

Relacionados con el problema de Guarini se han planteado otros problemas similares en los cuales se cambiaba el tamaño y forma del tablero de juego, y/o el número de caballos. La primera variante de este problema, para un tablero de tamaño 3 x 4, fue publicada en la revista Journal of Recreational Mathematics en 1974 (y posteriormente, en Scientific American en diciembre de 1978). El tablero y la posición inicial de la misma es la siguiente.

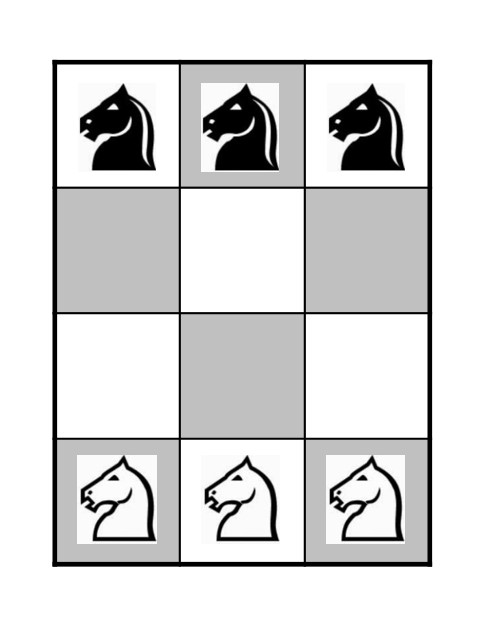
El método para resolverlo es de nuevo construir el grafo, de puntos y aristas, asociado al juego. Esta variante del problema de Guarini se transformaría en un problema de intercambio de fichas, tres blancas y tres negras, sobre la siguiente estructura estrellada.

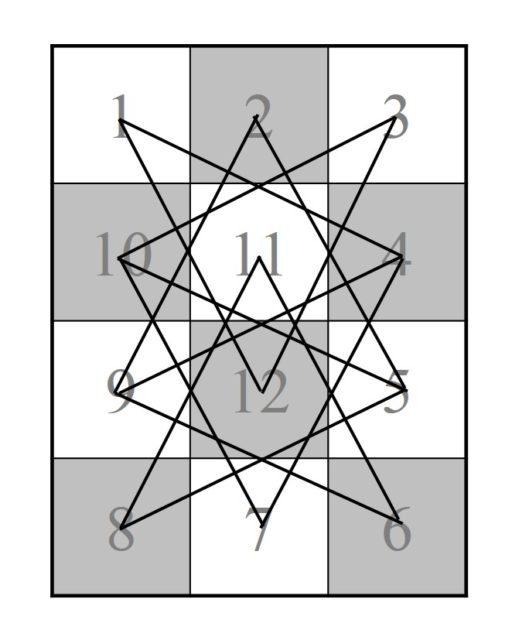
Aunque de nuevo debemos de deshacer el lío de las intersecciones de las aristas y simplificar el grafo, que ahora quedará de la siguiente forma.

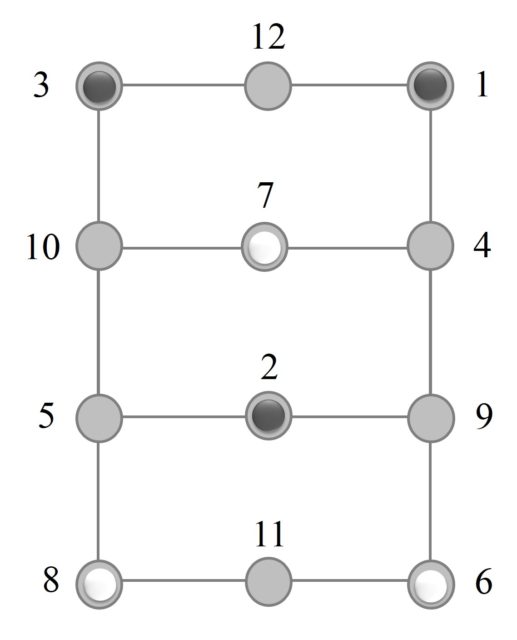
Ahora se pueden intercambiar las fichas blancas y negras en dieciséis movimientos. Para las fichas negras, la ficha de la casilla 1 va a la 6 (3 movimientos), de la 3 a la 7 (2 movimientos) y la de la 2 a la 8 (2 movimientos), en total serían 7 movimientos para las negras. Lo mismo para las blancas, otros 7 movimientos. El problema es que hay cruces entre las fichas blancas y negras, por lo que se necesitan dos movimientos más. En total dieciséis movimientos.

Para terminar con el contenido de esta entrada del Cuaderno de Cultura Científica os dejo planteadas otras dos variantes más.

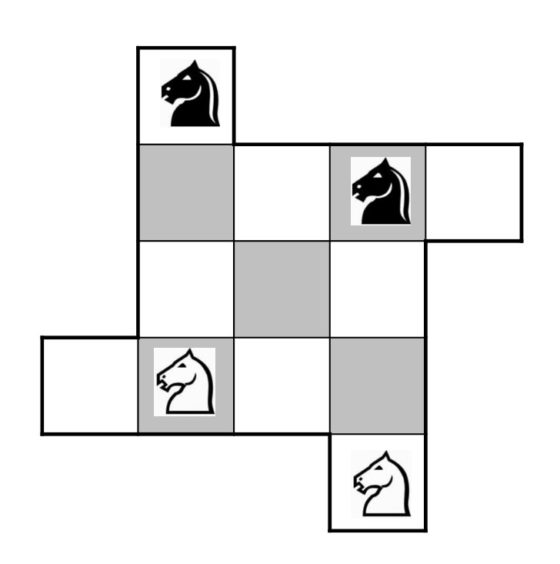
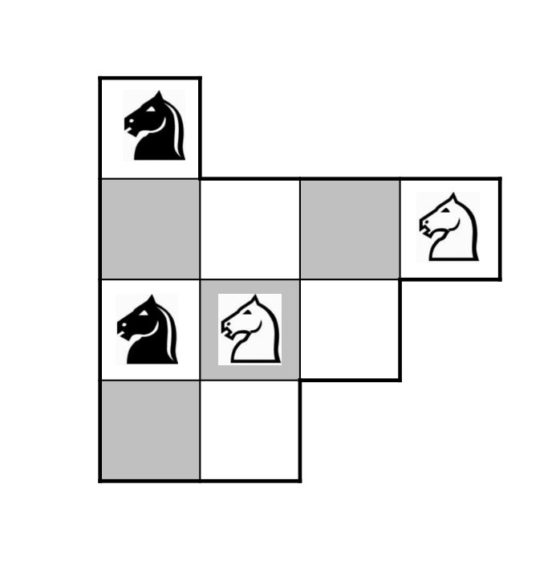
Las siguientes imágenes, que cierran esta entrada, son dos obras del artista británico Tom Hackney pertenecientes a sus series de obras geométricas que representan partidas de ajedrez del artista y ajedrecista francés Marcel Duchamp (1887-1968).

Bibliografía

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.

3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

4.- Ron Brown, The Use of the Knight’s Tour to Create Abstract, Leonardo, Vol. 25, No. 1, pp. 55 – 58, 1992.

5.- John J. Watkins, Across the board, The Mathematics of Chessboard Problems, Princeton University Press, 2004.

6.- Miodrag S. Petrovic, Mathematics and Chess, 110 Entertaining Problems and Solutions, Dover Publications, 1997.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica