Uno de mis libros preferidos de problemas y rompecabezas matemáticos es el libro Famous Puzzles of Great Mathematicians (Rompecabezas famosos de grandes matemáticos) del matemático Miodrag Petrovic. Uno de los problemas que aparecen en el apartado de aritmética es el siguiente problema del matemático indio del siglo IX Mahavira (o Mahaviracharya, es decir, “Mahavira el maestro”), que aparece en su libro Ganatasarasamgraha – Compendio de la esencia de las matemáticas–, del año 850:

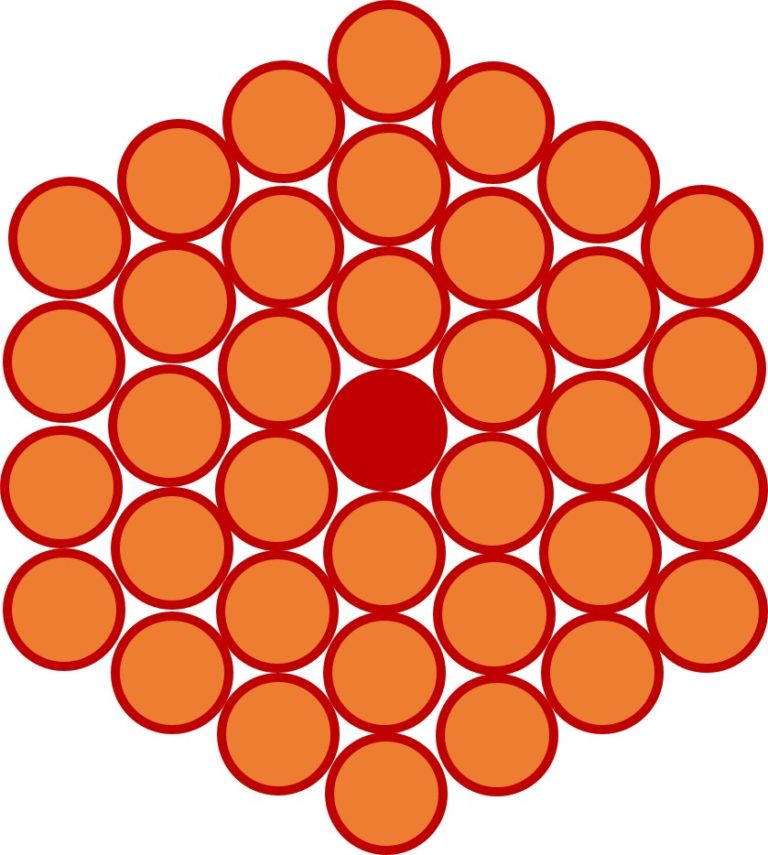
Problema: Las flechas, con forma de cilindros de sección circular, pueden ser empaquetadas formando un haz hexagonal. Si hay 18 flechas en la parte exterior del haz, determinar el número total de flechas que hay (en el haz) dentro del carcaj.

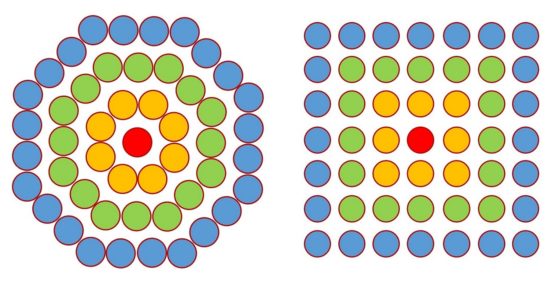
Este problema lo podemos resolver de una forma sencilla dibujando flechas (sus secciones circulares) formando una estructura hexagonal, como en la imagen siguiente. Podríamos proceder de forma ordenada. Primero 1 flecha en el centro, luego 6 alrededor formando un hexágono, después 12 en el siguiente hexágono alrededor del anterior, y finalmente 18 flechas en el hexágono exterior. Por lo tanto, la respuesta al problema es 1 + 6 + 12 + 18 = 37 flechas en total.

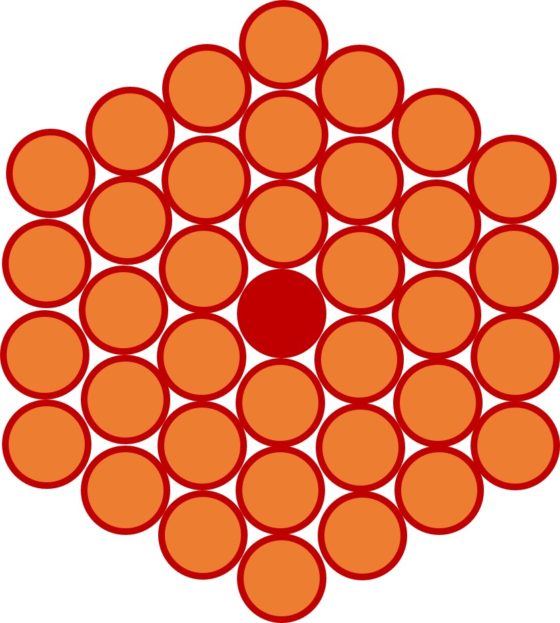
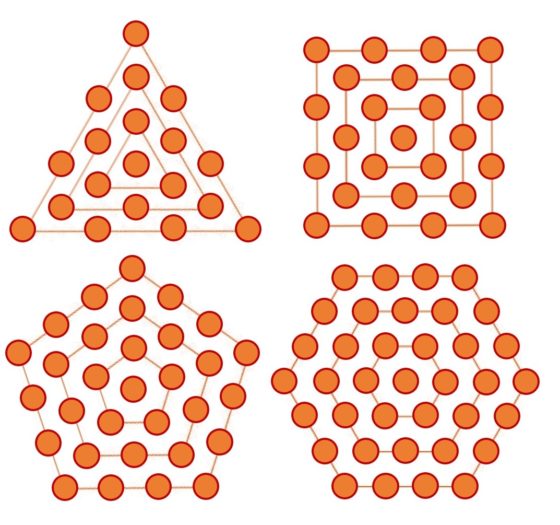
La solución de este problema está relacionada con los llamados números poligonales centrados. Como es bien conocido, los números poligonales (triangulares, cuadrados, pentagonales, hexagonales, etcétera) son aquellos números que se obtienen al representar el número como una disposición poligonal de puntos o piedras, como puede verse en la entrada El asesinato de Pitágoras, historia y matemáticas (y II). Sin embargo, existen otras disposiciones geométricas de puntos o piedras con forma poligonal, pero con un punto en el centro y los polígonos alrededor del mismo, son los números poligonales centrados (triangulares centrados, cuadrados centrados, pentagonales centrados, hexagonales centrados, etcétera).

Como puede verse en la siguiente imagen, los primeros números triangulares centrados son 1, 4, 10, 19, los cuadrados centrados son 1, 5, 13, 25, los pentagonales centrados 1, 6, 16, 31 y los hexagonales centrados, llamados por Martin Gardner números hex, 1, 7, 19, 37.

Si nos fijamos en la construcción de los números poligonales centrados, se ve rápidamente que se empieza por un punto, después se representa el polígono alrededor del punto y se van añadiendo polígonos cada vez más grandes. Por lo tanto, es fácil calcular el número de puntos que se necesitan para representar los polígonos centrados. En concreto, para un polígono de k lados, la fórmula para calcular los números poligonales centrados es:

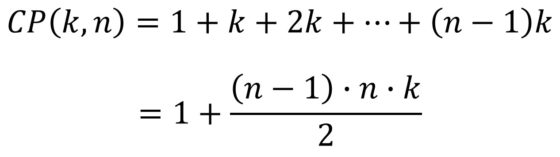
Pueden construirse fácilmente demostraciones sin palabras (véanse Matemáticas para ver y tocar y Más matemáticas para ver y tocar) de algunas primeras identidades de los números poligonales centrados.

Por ejemplo, se pueden relacionar los números cuadrados, pentagonales y hexagonales centrados con los números triangulares (los clásicos, no los centrados, sobre los que puede leerse en la entrada El asesinato de Pitágoras, historia y matemáticas (y II)): CC_n = 1 + 4T_{n – 1}, PC_n = 1 + 4T_{n – 1}, hex_n = 1 + 6T_{n – 1}, con la notación evidente.

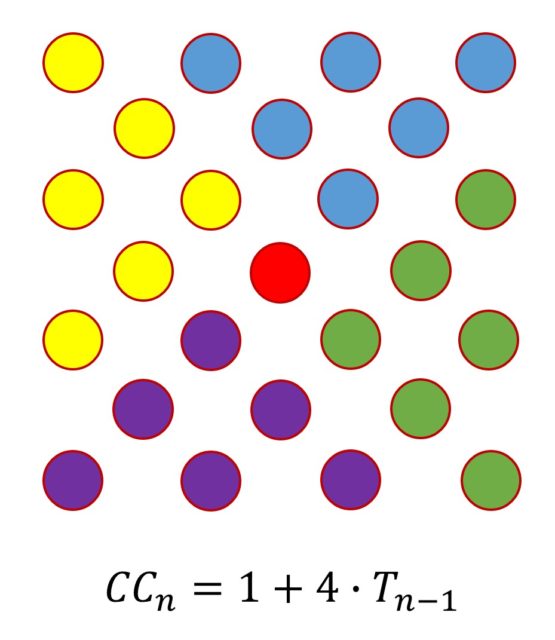
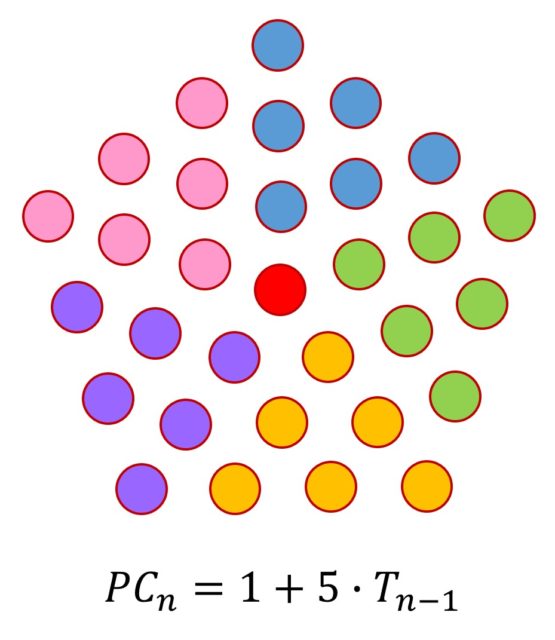
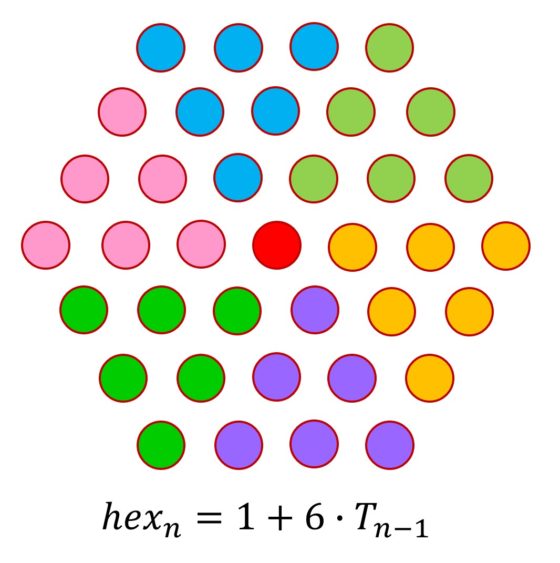
De hecho, esa es una identidad que se cumple para todos los números poligonales centrados, en concreto:

Pueden verse más identidades relacionadas con los números poligonales centrados. Para empezar, los números triangulares centrados (que forman la sucesión denominada A005448 en la Enciclopedia online de sucesiones de enteros, cuyos primeros veinte términos son 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, etcétera), pueden ser expresados como suma de tres números triangulares normales: TC_n = T_n + T_{n – 1} + T_{n – 2}, para n mayor o igual que 3.

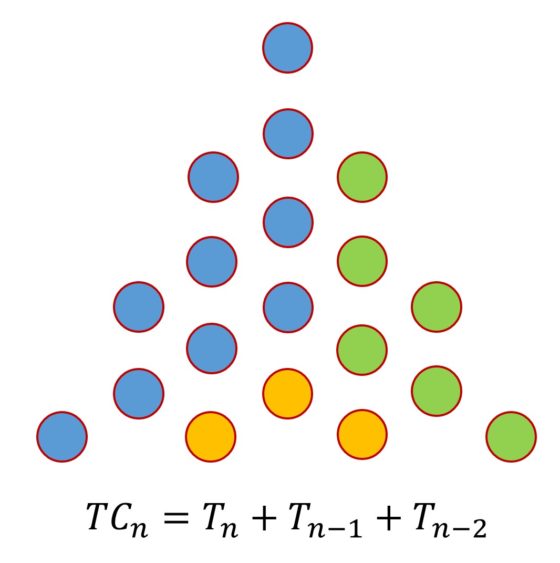
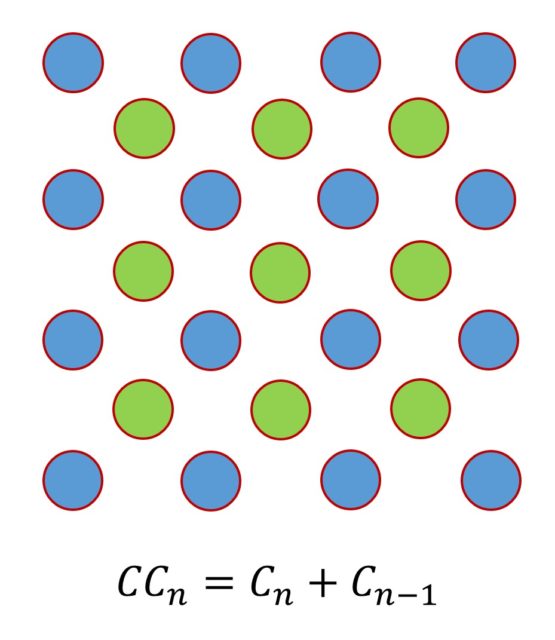
O los números cuadrados centrados (que forman la sucesión denominada A001844 en la Enciclopedia online de sucesiones de enteros, cuyos primeros veinte términos son 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, etcétera) pueden expresarse como suma de dos números cuadrados normales: CC_n = C_n + C_{n – 1}.

Los veinte primeros números pentagonales centrados, que es la sucesión A005891 en la Enciclopedia online de sucesiones de enteros son 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, etcétera. O la sucesión A003215 es la de los números hex, cuyos veinte primeros términos son 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, 1027, 1141, etcétera.

Pueden obtenerse también fórmulas para números poligonales centrados con una mayor cantidad de lados, por ejemplo, para los números octogonales centrados, se puede demostrar que son números cuadrados: OC_n = C_{2n – 1}.

Vamos a terminar esta entrada del Cuaderno de Cultura Científica con otro rompecabezas que aparece en el apartado de aritmética del libro Famous Puzzles of Great Mathematicians. Esta configuración mágica está contenida originalmente en el libro del matemático chino Yang Hui (aprox. 1238-1298) Xugu Zhaiqi Suanfa (Continuación de la tradición de extraños métodos de computación), de 1275.

Problema: Colocar los números del 1 al 33 en los pequeños círculos de la siguiente imagen, de forma que todos los números de las circunferencias concéntricas, incluido el centro, así como todos los números de los diámetros, sumen lo mismo.

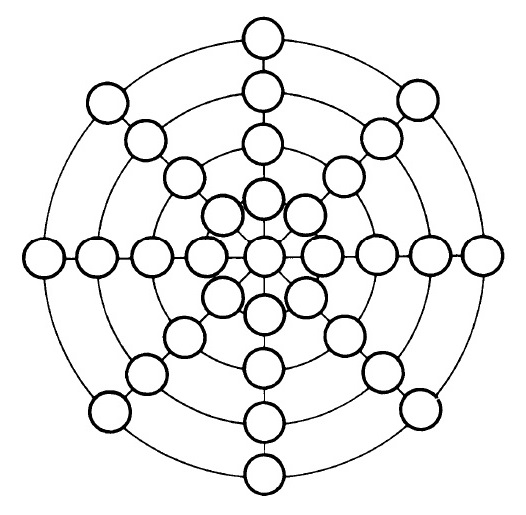
Este problema os lo dejo para quienes queráis enfrentaros al reto. ¡Que os divirtáis!

Bibliografía

1.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

2.- David Well, The Penguin Book of Curious and Interesting Puzzles, Penguin Books, 1992.

3.- John Conway, Richard K. Guy, The book of numbers, Springer-Verlag, 1996.

4.- Elena Deza, Michel Marie Deza, Figurative Numbers, World Scientific, 2012.

5.- Raúl Ibáñez, La gran familia de los números (título provisional), Catarata, 2020.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica