Teniendo en cuenta el interés que suscitó mi anterior entrada en el Cuaderno de Cultura Científica, Matemáticas para ver y tocar, me ha parecido interesante escribir una nueva entrada con más ejemplos de demostraciones visuales de fórmulas matemáticas sobre sumas de números.
Pero vamos a aprovechar esta entrada para realizar un mini homenaje a la persona que más ha hecho por la divulgación de las demostraciones gráficas, el matemático norteamericano Roger B. Nelsen, autor de la serie de libros Proofs without words (Demostraciones sin palabras), ya que él es el autor de todas las demostraciones para ver y tocar que vamos a mostrar en esta entrada.

En la anterior entrega vimos demostraciones para ver y tocar, haciendo uso de los pequeños cubos del material didáctico LiveCube, de las fórmulas para la suma de los primeros números naturales, de sus cuadrados o de los primeros números impares. En la presente entrada vamos a ver demostraciones gráficas de la fórmula que expresa el valor de la suma de los cuadrados de los números impares, del resultado matemático que dice de que todo cubo es suma de números impares consecutivos o de las sorprendentes sumas consecutivas de números consecutivos.
Empecemos con la fórmula de las sumas de los cuadrados de los números impares y la demostración sin palabras que realizó Roger B. Nelsen en 1994, publicada en College Mathematical Journal (vol. 25, no. 3, p. 246) y recogida en su segundo libro sobre Proofs without words. La fórmula dice…
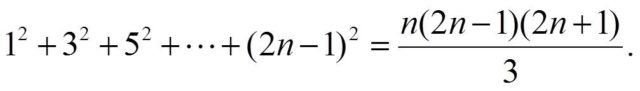
Para realizar esta demostración visual, a través del caso particular de n = 3, es decir, la suma de los cuadrados de los tres primeros números impares 1, 3 y 5 (en general, 12 + 32 + 52 + … + (2n – 1)2), empezamos precisamente con sencillas estructuras cuadradas con 12, 32 y 52 cubos (en general, estructuras cuadradas con hasta (2n – 1)2 cubos), cada una de las cuales son cortadas en dos partes como aparece en la imagen, en una parte verde y otra amarilla, para volverlas a unir de forma escalonada, de manera que generamos una nueva estructura de tipo piramidal (verde y amarilla en la imagen).

Una vez entendido este paso, debemos realizar tres copias de esta estructura, la verde y amarilla anterior, la roja que aparece en la imagen, que es igual a la anterior, y una azul que es esencialmente igual a las anteriores, salvo que está montada de forma simétrica, y es la imagen especular de la verde y amarilla, como se ve en la imagen.

Finalmente, se unen las tres estructuras, obteniéndose la nueva estructura que se muestra en la imagen.

Existen varias formas de contar los cubos que conforman esta estructura, que son tres veces nuestro objeto de deseo, la suma de los cuadrados de los primeros números impares, 12 + 32 + 52 + … + (2n – 1)2.
Una de las maneras, que no es la que nosotros vamos a realizar hoy aquí, sería hacer una copia de la estructura y colocarla, invertida, sobre la que ya tenemos, para formar un ortoedro, es decir, un prisma rectangular, con una base de 2n + 1 cubos de largo, 2n – 1 de ancho y 2n de alto. Luego, el número total de cubos del ortoedro es (2n + 1) (2n – 1)(2n) y el valor que nosotros buscamos la sexta parte de este, obteniéndose la fórmula.
Otra manera de contar el número de cubos de la estructura anterior es tener el cuenta que es (2n + 1) copias de la estructura que mostramos abajo, es decir, 1 + 2 + 3 + … + (2n – 1) cubos.

Luego en total, (2n + 1)(1 + 2 + 3 + … + (2n – 1)) cubos, de donde se deduce la fórmula para la suma de los cuadrados de los primeros números impares, 12 + 32 + 52 + … + (2n – 1)2.
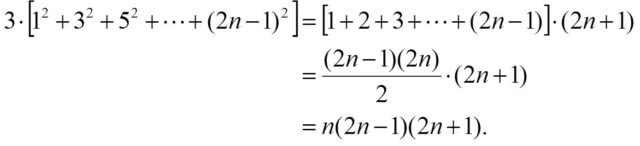
A continuación, vamos a mostrar una demostración sin palabras que Roger B. Nelsen realizó del siguiente resultado matemático: todo cubo es la suma de números impares consecutivos. Esta demostración apareció publicada en Mathematics Magazine (vol. 66, no. 5, 1993, p. 316) y se recoge en el primer volumen de Proofs without words.
Más aún, se demostrará que para un número cualquiera n, su cubo es igual a la siguiente suma de números impares consecutivos.
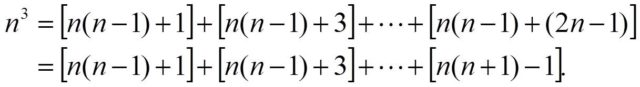
Veamos la demostración gráfica, ilustrando el caso particular de n = 5, que mostramos en las imágenes. Partimos de un cubo grande formado por 53 cubos (en general con n3 cubos), como el que aparece en la imagen.

Tomamos los cubos de la parte superior que aparecen en verde y los recolocamos encima de la estructura como aparece en la siguiente imagen.

Ahora dividimos la estructura resultante en secciones verticales, superficies planas con un grosor de un cubo, como aparecen en la imagen. Y contamos cuantos cubos hay en cada una de las secciones, la suma de todas ellas tiene que ser n3 (53 en el caso particular de la imagen).

En consecuencia, obtenemos la fórmula anterior, que nos expresa el cubo de cualquier número como suma de números impares consecutivos. Por ejemplo, para los 5 primeros números sería…
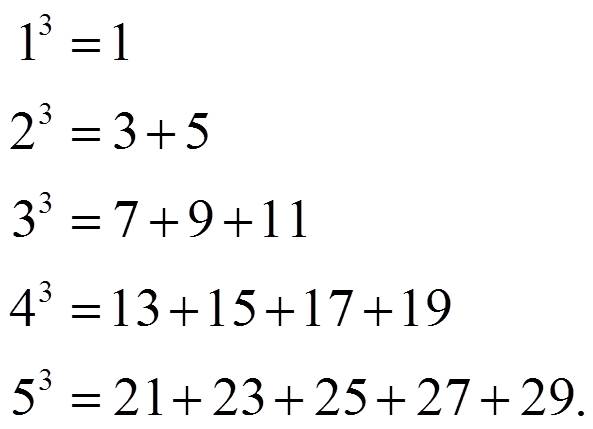
La última de las demostraciones tiene que ver con una de esas propiedades de los números que suele presentarse como mágica, una propiedad numérica expresada como sumas consecutivas de números consecutivos. Es una curiosa propiedad que llama la atención, como vemos en las siguientes sumas…
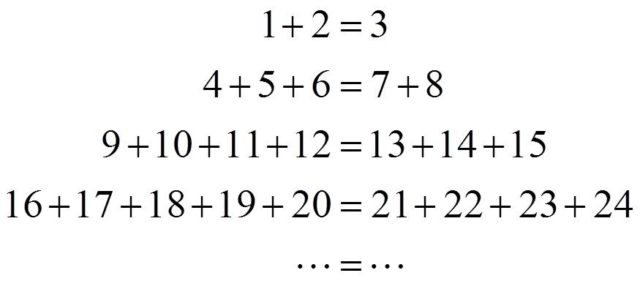
Y, de hecho, se puede generalizar en la siguiente fórmula.
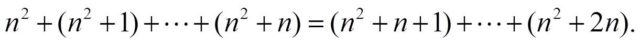
La siguiente demostración de esta curiosa propiedad se basa en la técnica del doble conteo, es decir, si contamos los elementos de un conjunto de dos formas distintas, el resultado debe ser el mismo. En realidad las fórmulas anteriores estaban basadas en gran medida en esta técnica.
El conjunto de partida para utilizar el conteo doble es el número de cubos de la siguiente estructura.

Para la primera forma de contar el número de cubos de esta estructura, con el objetivo de obtener la propiedad que estamos buscando, necesitamos separar la estructura en secciones verticales, cortando en la dirección que marcan los colores, como se ve en la siguiente imagen, generando secciones monocolor. Y así tenemos que la cantidad de cubos de la estructura es la suma de las cantidades de cada una de las secciones.

Para la segunda forma de contar los cubos se corta la estructura inicial en secciones verticales perpendiculares a las anteriores, quedando secciones bicolor. De nuevo, debemos calcular el número de cubos de cada sección, que podemos ver en la imagen.

Si tenemos en cuenta las dos cantidades obtenidas, que deben de ser iguales, se obtiene la fórmula deseada. Recordémosla…
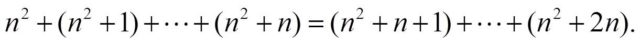
Esta demostración gráfica que aparece en el primero de los libros Proofs without words de Roger B. Nelsen, fue publicada por el mismo en Mathematics Magazine (vol. 63, no. 1, 1990, p. 25).

Bibliografía
1.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.
2.- Roger B. Nelsen, Proofs without words II, MAA, 2000.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Más matemáticas para ver y tocar …
[…] Teniendo en cuenta el interés que suscitó mi anterior entrada en el Cuaderno de Cultura Científica, Matemáticas para ver y tocar, me ha parecido interesante escribir una nueva entrada con más ejemplos de demostraciones… […]