¿Es áureo el Aston Martin de James Bond?
Esta semana, navegando por la red en busca de cierta información sobre el número de oro, acabé llegando a la página de Aston Martin, el coche del agente secreto 007, James Bond, desde que apareció por primera vez en la película “Goldfinger” (1964) hasta la que es la última entrega en la actualidad, “Skyfall” (2012). En esta página se afirma que la utilización de la razón áurea en los diseños de los coches Aston Martin es uno de los elementos que contribuye a su perfección,… “la razón áurea está en el corazón de cada Aston Martin”.

Si navegamos por la web de Aston Martin tres son los modelos en los que se indica explícitamente que se ha hecho uso de la divina proporción en su diseño, el modelo Rapide S (2013-2015), el nuevo modelo DB9 (2014) y el modelo V8 Vantage (2013).
Aunque quizás sea la razón áurea uno de los conceptos matemáticos más conocidos, vamos a empezar volviendo a recordar su definición (ya dedicamos una entrada de la sección Matemoción del Cuaderno de Cultura Científica a hablar de un par de proporciones, la raíz de dos y la razón áurea, en concreto aquella titulada “Visitad los museos, también en clave matemática”).
En esa entrada ya se comentaba que aunque parece ser que la proporción áurea fue estudiada por los pitagóricos, la primera definición aparece en el gran libro “Los Elementos” de Euclides (aprox. 325-265 a.c.). Y dice así:
“Se dice que un segmento está dividido en media y extrema razón cuando la longitud del segmento total es a la parte mayor, como la de esta parte mayor es a la menor”.
Si suponemos que la parte mayor del segmento tiene longitud 1 y el segmento x, entonces la parte menor es x – 1, de donde la condición para determinar el punto del segmento que lo divide en media y extrema razón es
y operando nos queda la ecuación de segundo grado . Cuya solución positiva, haciendo uso de la conocida fórmula para resolver ecuaciones de segundo grado, es igual a
Esta sencilla razón es la que posteriormente acabaría llamándose número de oro, razón áurea o divina proporción, y que se suele denotar por la letra griega phi, .
Y por lo tanto, un rectángulo, en particular, el lienzo de un cuadro, se dice que es un rectángulo áureo si la proporción entre su ancho, p, y su alto, q, es precisamente la razón áurea,
. En la mencionada entrada del Cuaderno de Cultura Científica se pueden ver además algunas propiedades de la divina proporción y su presencia en algún cuadro.
Pero lo que nos interesa hoy aquí es esa idea que maneja el fabricante de automóviles británico Aston Martin, según la cual la razón áurea está relacionada con la perfección y la belleza. A lo largo del siglo XX, y continúa en el siglo XXI, la divina proporción ha sido ampliamente utilizada en el mundo del arte (Juan Gris, Marcel Duchamp, Piet Mondrian, Josef Albers, Max Bill, Salvador Dalí o Maruja Mallo, entre otros), la arquitectura (Le Corbusier o Mario Botta) o el diseño (Mies Van der Rohe, Eero Saarinen o Jan Tschichold), como un medio de dotar a la obra, a través de esas medidas, de perfección y belleza.

El origen del enorme éxito de este concepto matemático, el número de oro, está seguramente en los trabajos del físico y psicólogo alemán Gustav Fechner (1801-1887) sobre la belleza del rectángulo áureo, los estudios sobre las proporciones dinámicas del artista canadiense Jay Hambidge (1867-1924), pero sobre todo, los libros “Estética de las Proporciones en la Naturaleza y en las artes” (1927) y “El número de oro” (1931) del polifacético rumano Matila Ghyka (1881-1965), y que tuvieron un gran impacto en el mundo de la cultura. Independientemente de la veracidad de lo expuesto en esos trabajos (tema al que dedicaremos alguna entrada en el futuro), lo cierto es que calaron muy hondo en la sociedad, y sobre todo, en el mundo del arte. Y en esta realidad actual es en la que estamos interesados en la presente entrada.
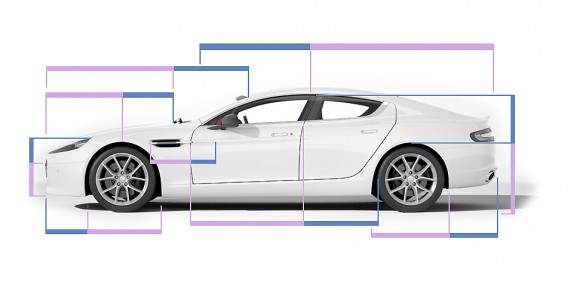
Pero volviendo a la presencia de la divina proporción en los coches Aston Martin, vemos que en los modelos Rapide S y el nuevo DB9, se justifica la presencia de esta proporción, e incluso se acompaña con unas imágenes indicando el uso de la misma en el diseño exterior de los coches.
Para empezar, en el modelo Rapide S hay un apartado bajo el nombre “Arrebatadoras proporciones” que dice lo siguiente:
“Breathtaking proportions: The ‘Golden Ratio’ sits at the heart of every Aston Martin. Balanced from any angle, each exterior line of Rapide S works in concert and every proportion is precisely measured to create a lithe, pure form. Our engineering follows the same principle. A near perfect weight distribution ensures Rapide S is balanced in form and balanced in function”.
Como decíamos al principio, está dando una gran importancia a la proporción áurea en el diseño de los Aston Martin, al decir que “la razón áurea está en el corazón de cada Aston Martin” y continúa diciendo que en el diseño del model Rapide S “cada proporción está medida con precisión para crear una forma ágil y pura”.
O en el nuevo modelo DB9 de Aston Martin se dice:
“Perfectly proportioned: Every inch of DB9’s form is designed for elegance and balance. The simple beauty of nature guides the design of DB9, with the ‘golden ratio’ setting all proportions. The result is a profile where every line, dimension and proportion works in harmony. Combine this with the near perfect weight distribution, provided by a lower engine placement, and you have a DB9 balanced on sight and in experience”.
Vemos de nuevo la importancia que se le da a la proporción, a la armonía, de la mano de la razón áurea. Podemos leer que “la sencilla belleza de la naturaleza guía el diseño del DB9, con la razón áurea marcando todas las proporciones” y que “el resultado es un perfil donde cada línea, dimensión y proporción funcionan en armonía”.

Como decíamos anteriormente, este ejemplo de la presencia de la razón áurea en los diseños (o, al menos, en la explicación de los mismos) de los coches Aston Martin, no es más que un ejemplo del interés que hoy en día tienen artistas y diseñadores en esta proporción. Y vamos a continuar con otro ejemplo muy visual, el libro “Golden Meaning. Fifty-five graphics experiments” (GraphicDesign, 2014). En el libro se recogen 55 obras (notemos que el número 55 es un número de la sucesión de Fibonacci, que es una sucesión en la que cada número se obtiene como suma de los dos anteriores 1 1 2 3 5 8 13 21 34 55… y que aparece, por ejemplo, en la filotaxis y en el arte (véase “¡Póngame media docena de fibonaccis!”); esta sucesión está fuertemente relacionada con la divina proporción, puesto que los cocientes de números consecutivos de la sucesión de Fibonacci 2/1, 3/2, 5/3, 8/5, 13/8, 21/13,… convergen al número phi) de diseñadores, tipógrafos y artistas, que intentan comunicar, explorar o explicar la proporción áurea. La introducción del libro está escrita por el divulgador de las matemáticas Alex Bellos, autor del libro “Alex en el país de los números” (Grijalbo, 2011). Cada diseño gráfico se acompaña además con una explicación de su autor.

Veamos algunos ejemplos. El primero que mostramos se debe a los diseñadores gráficos Bibliothèque , que nos muestran lo que podíamos denominar la “temperatura áurea” y la “hora áurea”. Este primer ejemplo se apoya directamente en la definición de la divina proporción. En el primero, el mercurio estaría marcando la temperatura tal que divide al segmento de posibles temperaturas “en media y extrema razón”. En el caso del reloj, las agujas pequeña (para las horas, y situada en las 12) y grande (la de los minutos) forman el ángulo áureo, que no es más que el ángulo que divide a la circunferencia, de hecho al segmento 0-360º, de acuerdo con la sección áurea. Si el ángulo es x, el ángulo opuesto es 360º-x, y su cociente será el número de oro (360º-x)/x = 1,6180339887.., de donde el ángulo es aproximadamente x = 137,5º. Este ángulo tiene una gran importancia en la filotaxis, y en particular, en la distribución de las semillas en las cabezas de los girasoles, pero ya hablaremos de ese tema en alguna otra ocasión. Pero volviendo al reloj… ¿ qué hora será la que marca ese reloj? Si tenemos en cuenta que una vuelta entera de la aguja grande son 60 minutos, entonces la aguja grande está marcando casi 23 minutos, luego son las 12:23.

El segundo ejemplo que mostramos aquí, del ilustrador Laurence Zeegen, es muy sencillo y está relacionado con el concepto de rectángulo áureo. En él se puede ver cómo un hombre, que como dice su autor podría ser un pintor, un profesor de arte o un decorador, está pintando con una brocha un rectángulo áureo.

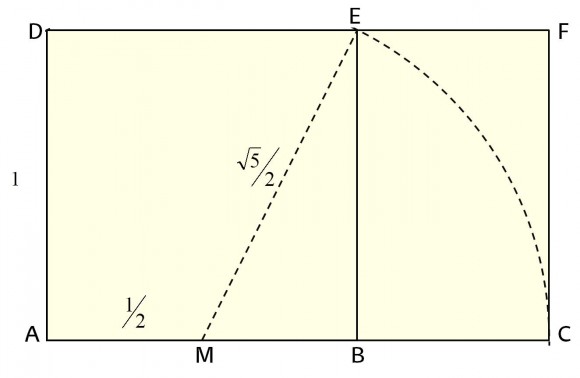
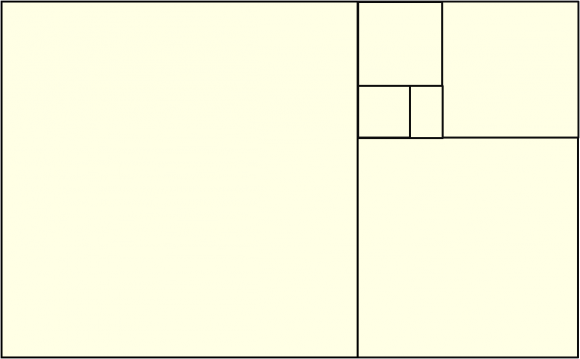
Para los siguientes diseños que queremos mostrar, necesitamos recordar la red de cuadrados y rectángulos áureos, asociados a un rectángulo áureo inicial, así como la espiral áurea que se genera a partir de la misma. Si le damos la vuelta a la construcción que hemos visto anteriormente de un rectángulo áureo a partir de un cuadrado (véase la imagen), resulta que cualquier rectángulo áureo puede descomponerse en un cuadrado y un rectángulo áureo más pequeño. Y si continuamos esta descomposición con este nuevo rectángulo áureo, se construye un entramado de cuadrados y rectángulos áureos dentro del rectángulo inicial, como se muestra en la imagen.
A partir de esta descomposición se construye la espiral áurea como unión de arcos de circunferencias dibujamos sobre el entramado anterior (véase la siguiente imagen).
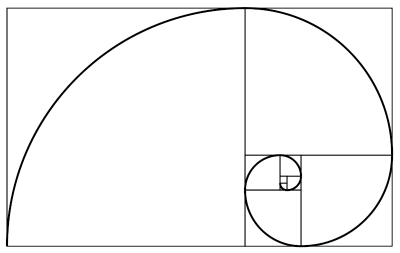
Relacionado con el concepto de espiral áurea y la división del rectángulo áureo en un entramado de cuadrados y rectángulos, está el trabajo de los diseñadores gráficos polacos Homework, que lleva por título “Golden ass” (culo áureo). Además, el “culo áureo” está acompañado de una tipografía al estilo de los años 1970 realizada con los trozos de la espiral.

El diseñador inglés Adrian Talbot también diseña una tipografía especial para este libro, basada en el rectángulo áureo, y más concretamente en la descomposición en cuadrados y rectángulos.

La diseñadora francesa, afincada en Londres, Margot Lombaert también utiliza la espiral áurea, y las circunferencias que dan lugar a la misma, en su diseño para el libro “Golden Meaning”.


Y terminamos con el interesante diseño del austriaco Tomi Vollauschek que incluye los 10.000 primeros decimales del número de oro o las espirales áureas.

Bibliografía
1.- James Bond y los coches Aston Martin
2.- Aston Martin, modelo Rapide S
3.- Aston Martin, nuevo modelo DB9
4.- Aston Martin, modelo V8 Vantage
5.- Mario Livio, La proporción áurea, la historia de phi, el número más sorprendente del mundo, Ariel, 2006.
6.- Matila Ghyka, “Estética de las Proporciones en la Naturaleza y en las artes”, Poseidón, 1983.
7.- Matila Ghyka, “El número de oro”, Poseidón, 1992.
8.- VVAA, Golden Meaning. Fifty-five graphics experiments, GraphicDesign, 2014.
9.- Artículo de Alex Bellos para The Guardian, Golden Meaning: graphic artists depict the golden ratio – in pictures
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica


Juan Carlos M. Cancela
Qué capacidad tenemos los humanos para montar tinglados. Una proporción es una proporción. Se puede decir de la 1,618… que es bella, ágil, pura o divina. Y se puede decir exactamente lo mismo (o lo contrario) de la 1,5 o de la 1,333…
Si el saldo en tu tarjeta de crédito (que también tiene esa proporción) te da para un Aston Martin y te apetece comprártelo, hazlo. Y si el que te gusta no es el Aston Martin no sufras porque no sea áureo. La mayoría de tus congeneres no tienen la suerte de poder hacerse esos líos.
¿Es áureo el Aston Martin de James Bond?
[…] ¿Es áureo el Aston Martin de James Bond? […]
Hitos en la red #41 | Naukas
[…] por Antonio Martínez Ron y Javier Peláez. A veces es incluso expresable matemáticamente, ¿Es áureo el Aston Martin de James Bond?, de Raúl […]
Matemática punk, un homenaje a Calpurnio — Cuaderno de Cultura Científica
[…] la banda de Moebius, la cuarta dimensión, la escalera infinita de Escher, el efecto mariposa, la espiral áurea, los números, el tangram (que podéis ver en la siguiente imagen), el infinito, los diagramas […]
Una banda de Moebius de chocolate — Cuaderno de Cultura Científica
[…] de un rectángulo áureo (véanse las entradas Visitad los museos, también en clave matemática, ¿Es áureo el Aston Martin de James Bond? o Crímenes áureos). Por otra parte, las mousses, de chocolate, de avellana y de coriandro, iban […]
Los fonones de los cuasicristales y la proporción áurea — Cuaderno de Cultura Científica
[…] menor a energías de fonón específicas que están relacionadas entre sí a través de la proporción áurea, una constante matemática que también está vinculada a la geometría de la red no periódica de […]
ECHO, un cómic áureo — Cuaderno de Cultura Científica
[…] de Cultura Científica en algunas entradas como Visitad los museos, también en clave matemática, ¿Es áureo el Aston Martin de James Bond? ó Crímenes […]